19 Mikroekonomie by xnovm148

CHOVÁNÍ FIRMY NA TRHU VÝROBKŮ A SLUŽEB

- délka období - není to otázka času, ale je to otázkou toho, jestli jsou vstupy variabilní, můžeme

jednotlivě kombinovat, nebo jestli jsou nějaké vstupy fixní

- velmi krátké období – firmy nemohou měnit vstupy, nic nelze měnit, nabídka se nestačí přizpůsobit

- období velmi dlouhé – projev technického rozvoje » vliv variability vstupů + jejich vývoj

1. KRÁTKÉ OBDOBÍ

= takové období kdy je aspoň jeden fixní vstup → kapitál (K) je fixní vstup, práce (L) je vstup

variabilní (nebo objem produkce – rozsah kapacity) → začné se prosazovat zákon klesajících výnosů,

respektive výnosy z variabilního vstupu a ty mohou být:

a) rostoucí výnosy – situace, když roste variabilní vstup o jedno procento

(práce) tak produkt roste o víc než jedno procento

b) konstantní výnosy – platí, když roste variabilní vstup o jedno procento, tak

produkt poroste také o jedno procento

c) klesající výnosy – taková situace, když se zvýší variabilní vstup o jedno

procento, tak produktu poroste méně než jedno procento

1.1 - Produkční funkce

- vztah mezi vstupy a výstupy

- vyjadřuje maximální objem produkce, který můžeme vyrobit s danou kombinací výrobních

faktorů při dané technologii

Q = f (f1, f2....fn) = > produkční funkce je funkcí jednotlivých výrobních faktorů

- funkci chápeme:

• celkový fyzický produkt … TPP

= celkové množství statků (produkce), které bylo vyrobeno za jisté

časové období vyrobenou danou technologií a výrobními faktory ve

fyzických jednotkách (jednotky – kusy) TPP = Q → vztah

• průměrný fyzický produkt … APP

= množství produkce, které připadá na jednu jednotku variabilního vstupu

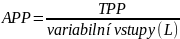
• mezní fyzický produkt … MPP

= změna celkového produktu

- jednotky - kusy/varibailní vstupy

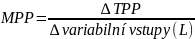
- předpokládáme v té naší produkční funkcí a

Ss v celém výkladu nejprve rostoucí výnosy

z variabilního vstupu a po té klesající výnosy z variabilního vstupu (zákon kles.výnosů)

- vychází ten graf ze zákona klesajích výnosů – podle něj

s růstem množství jednoho vstupu jeho mezní výnosy

snižují, protože zkoumáme důsledky změn množství

jednoho vstupu, hovoříme o výnosech z variabilního

vstupu

Rostoucí výnosy:

- každá další jednotka přináší APP rostoucí MPP

↑ MPP → TPP ↑ rychleji než variabilní vstupy

Klesající výnosy:

↓ MPP → TPP ↑ pomaleji než množství var.vstupů

MPP = 0

TPP je maximální

Obrázek 1 - produkční funkce

MPP je záporný → TPP klesá

1.2 - Nákladová funkce - !!! vždycky z produkční funkce vyvozujeme nákladovou funkci !!!

- náklady jsou inverzní vůči produkční funkci

= finanční prostředky vynaložené na vstupy (na výrobu dané produkce) a to:

1. explicitní = skutečné náklady, evidované v účetnictví – náklady za mzdy, materiál atd.

2. i mplicitní = neskutečné náklady, např. náklady obětované příležitosti = alternativní náklady. Vyplývají z VF ve vlastnictví majitele firmy (např. mzda majitele, který by se nechal zaměstnat)

Ekonomické pojetí → celkové ekonomické náklady

• celkové ekonomické náklady jsou součtem explicitních a implicitních, v ekonomickém pojetí (C = costs)

• např. vlastním pole, ale nepoužívám ho nebo zvažují o pronájem – případný pronájem by byl tímto nákladem

- náklady jsou:

• celkové náklady … TC TC = FC + VC

= množství peněz, které je nutno vynaložit na vyrobení jistého objemu produkce

• fixní náklady (FC) = náklady které se nemění s rozsahem

produkce, firma je musí vynaložit, i když je vůbec nevyrábí

(najme si nějakou dílnu a majiteli dílny je jedno jestli tam

někdo dělá nebo nedělá, platí se pořád)

• variabilní náklady (VC) = náklady, které se mění s rozsahem produkce

• průměrné náklady … AC AC = AFC + AVC

= náklady, které připadají na jednu jednotku celkové produkce (Kč/Q -jednotka)

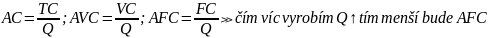
• průměrné fixní náklady (AFC) – budou klesat s rozsahem produkce,

celkovou částku rozpočtu na celkový objem produkce

• průměrné variabilní náklady (AVC) – mění se s rozsahem produkce

• mezní náklady … MC

= směrnice celkových nákladů

= objem nákladů, který připadá na dodatečnou jednotku produkce

- závisí na VC !

z  TPP vyvozujeme VC – v krátkém období

VC při rostoucích výnosech:

↑MP, ↑VC pomaleji než objem produkt

VC při klesajících výnosech:

↓MP, ↑VC rychleji než produkce (množství),

TC↑ pomaleji

Tvar křivky TC je stejný jak VC, FC náklady

ovlivňují konkrétní výši TC (polohu křivky TC

ovlivňují) nikoliv tvar křivky

z APP vyvozujeme AVC

APP ↑ → AVC AC < MC → AC ↑

APP ↓ → AVC ↑ AC > MC → AC ↓

AC = AFC ↓ pořád + AVC MC > AVC → AVC ↑

AVC a AC – tyto dva se k sobě přibližují

MP ↑ → MC ↓ a naopak

M

Obrázek 2 - Nákladová funkce

C protínají AVC a AC v minimum

APP je inverzní AVC tzn. maximum APP odpovídá min AVC !!!

Čím jsou determinovány náklady v krátkém období? Proč mají ten tvar, který mají (APP a AVC asi)

• závisí na variabilních vstupech – výnosy z variabilního vstupu, respektive zákonem klesajících výnosů

• jak produkční tvar, tak i náklad. fce je determinována podle toho jak se tam projevuje zákon kles.výnosů

2. Dlouhé období

- takové období, kde jsou všechny vstupy variabilní (výroba se mění díky všem vstupům) – kapitál (K)

a práce (L) jsou variabilní → a tím hovoříme o výnosech z rozsahu (=situace, kdy se mění

proporcionálně kapitál o jedno procento, práci o jedno procento…všechny vstupy a ptáme se

jaký efekt to bude mít na produkt)

- výnosy z rozsahu dělíme:

a) rostoucí výnosy z rozsahu – zvýšíme všechny vstupy o jedno procento, tak

produkt roste o víc než jedno procento

b) konstantní výnosy z rozsahu – všechny vstupy zvýšíme o jedno procento, tak

produkt poroste také o jedno procento

c) klesající výnosy z rozsahu – všechny vstupy se zvýší o jedno procento, tak

produktu poroste méně než jedno procento

2.1 - Produkční funkce

- je charakterizována výnosy z rozsahu a vzájemnou nahraditelností, substituce vstupů

= vyjadřuje maximální množství produkce, které je možno vyrobit různou kombinací vstupů

(výrobních faktorů) při dané technologii

- máme dva vstupy: práci a kapitál – variabilní vstupy

- neplatí zákon klesajících výnosů

- izokvanta – vyjadřuje kombinaci výrobních faktorů, pomocí nichž lze vyrobit stejný

objem produkce

- grafických znázorněním dlouhodobé produkční funkce je celá mapa izokvanty

- indiferenční analýza znamená neměřitelnost užitku a mapa izokvanty je

měřitelnost

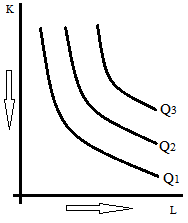
Q = f(K,L)

K » kapitál

L » práce (labour)

– Δ K . MPP_K = Δ L . MPP_L