
- •Эконометрическая модель.
- •Измерения в экономике. Шкалы измерений.
- •Случайные события и случайные переменные. Распределение случайных величин.
- •Статистические характеристики случайных величин и их свойства.
- •Основные функции распределения.
- •Оценки статистических характеристик и их желательные свойства.
- •Проверка статистических гипотез.
- •Критерий и критическая область.
- •Мощность статистического критерия. Уровень значимости.
- •Модель линейной регрессии.
- •Оценивание параметров регрессии. Метод наименьших квадратов.
- •Система нормальных уравнений мнк и ее решение.
- •Свойства оценок параметров, полученных методом наименьших квадратов. Условия Гаусса – Маркова.
- •Коэффициент детерминации и его свойства.
- •Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия.
- •Доверительные интервалы оценок параметров и проверка гипотез об их значимости.
- •Прогнозирование по регрессионной модели и его точность. Доверительные и интервалы прогноза.
- •Ковариационная матрица оценок коэффициентов регрессии.
- •Проверка значимости коэффициентов и адекватности регрессии для множественной линейной регрессионной модели.
- •Коэффициент множественной детерминации. Скорректированный коэффициент детерминации.
- •Проблемы спецификации регрессионной модели. Пошаговая регрессия.
- •Проблема смещения Предположим, что переменная у зависит от двух переменных х1, и х2 в соответствии с соотношением:
- •Неприменимость статистических тестов
- •Замещающие переменные. Фиктивные переменные.
- •Мультиколлинеарность. Влияние мультиколлинеарности на оценки параметров уравнения регрессии.
- •Методы борьбы с мультиколлинеарностью.
- •Линеаризация регрессионных моделей путем логарифмических преобразований.
- •Модели с постоянной эластичностью. Производственная функция Кобба - Дугласа.
- •Модель с постоянными темпами роста (полулогарифмическая модель).
- •Полиномиальная регрессия.
- •Кривая Филипса
- •Гетероскедастичность. Последствия гетероскедастичности для оценок параметров регрессии методом наименьших квадратов и проверки статистических гипотез.
- •Признаки гетероскедастичности и ее диагностирование. Обнаружение гетероскедастичности
- •1. Графический анализ остатков
- •2. Тест ранговой корреляции Спирмена
- •3. Тест Голдфелда-Квандта
- •Оценивание коэффициентов множественной линейной регрессии в условиях гетероскедастичности. Обобщенный метод наименьших квадратов.
- •Автокорреляция. Причины автокорреляции.
- •Влияние автокорреляции на свойства оценок мнк.
- •Тест серий. Статистика Дарбина – Уотсона.
- •Способы противодействия автокорреляции.
- •Стохастические объясняющие переменные. Последствия ошибок измерения.
- •Инструментальные переменные.
- •Лаговые переменные и экономические зависимости между разновременными значениями переменных.
- •Модели с распределенными лагами.
- •Модели авторегрессии как эквивалентное представление моделей с распределенными лагами.
- •Ожидания экономических агентов и лаговые переменные в моделях
- •Модели наивных и адаптивных ожиданий.
- •Модель гиперинфляции Кейгана.
- •44. Модель гиперинфляции Кейгана
- •Понятие об одновременных уравнениях. Структурная и приведенная форма модели.
- •Структурная и приведённая форма. Идентифицируемость
- •Примеры
- •Проблема идентификации. Неидентифицируемость и сверхидентифицированность.
- •Оценивание системы одновременных уравнений. Косвенный и двухшаговый мнк.
- •Системы эконометрических уравнений с лаговыми переменными.
- •Модель Кейнса.
- •Модель Клейна.
- •Матричная форма записи модели Клейна
Коэффициент детерминации и его свойства.
Для
оценки качества подбора линейной функции
рассчитывается квадрат линейного
коэффициента корреляции
![]() ,
называемый коэффициентом
детерминации.
Коэффициент детерминации характеризует
долю дисперсии результативного признака
y,
объясняемую регрессией, в общей дисперсии
результативного признака:
,
называемый коэффициентом
детерминации.
Коэффициент детерминации характеризует
долю дисперсии результативного признака
y,
объясняемую регрессией, в общей дисперсии
результативного признака:
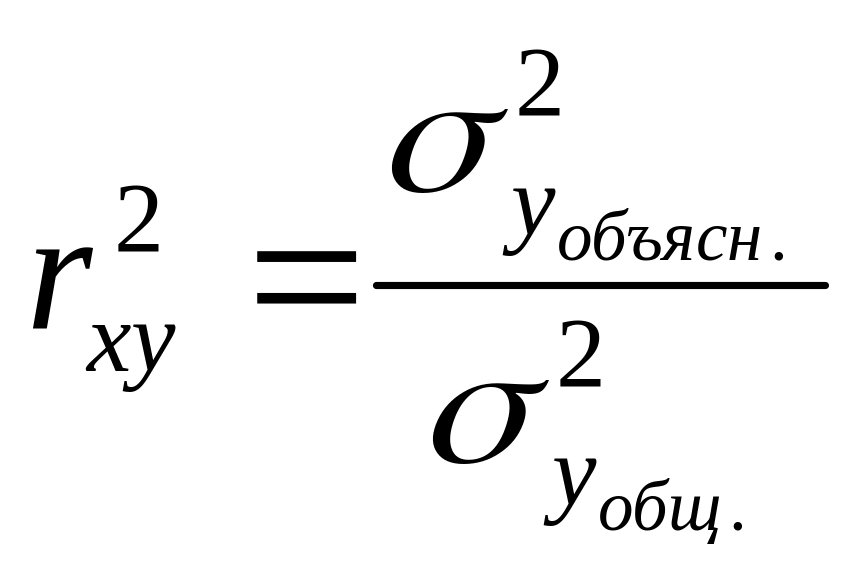
Соответственно величина 1 - характеризует долю дисперсии y, вызванную влиянием остальных не учтенных в модели факторов.
Например = 0,982. Таким образом, уравнением регрессии объясняется 98,2% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,8% ее дисперсии (т.е. остаточная дисперсия). Величина коэффициента детерминации является одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов и, следовательно, линейная модель хорошо аппроксимирует исходные данные, и ею можно воспользоваться для прогноза значений результативного признака.
![]() (получается
при разложении дисперсии)
(получается
при разложении дисперсии)
Максимальное
значение коэффициента R2
равно единице. Это происходит в том
случае, когда линия регрессии точно
соответствует всем наблюдениям, так
что
![]() ,
для всех i
и все остатки равны нулю. Тогда
,
для всех i
и все остатки равны нулю. Тогда
![]() и R2=1.
и R2=1.
Если в выборке отсутствует видимая связь между у и х, то коэффициент R2 будет близок к нулю.
При прочих равных условиях желательно, чтобы коэффициент R2 был как можно больше. В частности, мы заинтересованы в таком выборе коэффициентов а и Ь, чтобы максимизировать R2. Не противоречит ли это нашему критерию, в соответствии с которым а и b должны быть выбраны таким образом, чтобы минимизировать сумму квадратов остатков? Нет, легко показать, что эти критерии эквивалентны, если (используется как определение коэффициента R2.
Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия.
Предложение об ошибках в классической модели формируются наиболее жестким и не всегда реалистичным путем:
Предполагается,
что ошибка (![]() (
= 1 … N))
образует так называемый слабый белый
шум – последовательность центрированных
(
(
= 1 … N))
образует так называемый слабый белый
шум – последовательность центрированных
(![]() )
и не коррелированных случайных величин
с одинаковыми дисперсиями
)
и не коррелированных случайных величин
с одинаковыми дисперсиями
![]()
Свойство
центрированности практически не является
ограничением, так как при наличии
постоянного регрессора среднее значение
ошибки можно было бы включить в
соответствующий коэффициент (![]() )
)
В ряде случаев сделанные предложения об ошибках будут дополняться свойствами нормальности – случайный вектор имеет нормальное распределение. Эту модель мы будем называть классической моделью с нормально распределительными ошибками.
Многомерное
нормальное распределение задается
своим вектором и матрицей ковариации
– здесь она имеет вид
![]() ,
где 1 – единичная матрица. Если компоненты
вектора корелированы, следовательно,
автоматически независимы, следовательно,
ошибки в модели образуют последовательность
независимых одинаково нормально
распределенных случайных величин N
(0;
,
где 1 – единичная матрица. Если компоненты
вектора корелированы, следовательно,
автоматически независимы, следовательно,
ошибки в модели образуют последовательность
независимых одинаково нормально
распределенных случайных величин N
(0;![]() ).
).
Если каждая из величин нормально распределена, то вектор , из них составленный, ну обязан быть нормально распределенным.
