
- •Эконометрическая модель.
- •Измерения в экономике. Шкалы измерений.
- •Случайные события и случайные переменные. Распределение случайных величин.
- •Статистические характеристики случайных величин и их свойства.
- •Основные функции распределения.
- •Оценки статистических характеристик и их желательные свойства.
- •Проверка статистических гипотез.
- •Критерий и критическая область.
- •Мощность статистического критерия. Уровень значимости.
- •Модель линейной регрессии.
- •Оценивание параметров регрессии. Метод наименьших квадратов.
- •Система нормальных уравнений мнк и ее решение.
- •Свойства оценок параметров, полученных методом наименьших квадратов. Условия Гаусса – Маркова.
- •Коэффициент детерминации и его свойства.
- •Предположение о нормальном распределении случайной ошибки в рамках классической линейной регрессии и его следствия.
- •Доверительные интервалы оценок параметров и проверка гипотез об их значимости.
- •Прогнозирование по регрессионной модели и его точность. Доверительные и интервалы прогноза.
- •Ковариационная матрица оценок коэффициентов регрессии.
- •Проверка значимости коэффициентов и адекватности регрессии для множественной линейной регрессионной модели.
- •Коэффициент множественной детерминации. Скорректированный коэффициент детерминации.
- •Проблемы спецификации регрессионной модели. Пошаговая регрессия.
- •Проблема смещения Предположим, что переменная у зависит от двух переменных х1, и х2 в соответствии с соотношением:
- •Неприменимость статистических тестов
- •Замещающие переменные. Фиктивные переменные.
- •Мультиколлинеарность. Влияние мультиколлинеарности на оценки параметров уравнения регрессии.
- •Методы борьбы с мультиколлинеарностью.
- •Линеаризация регрессионных моделей путем логарифмических преобразований.
- •Модели с постоянной эластичностью. Производственная функция Кобба - Дугласа.
- •Модель с постоянными темпами роста (полулогарифмическая модель).
- •Полиномиальная регрессия.
- •Кривая Филипса
- •Гетероскедастичность. Последствия гетероскедастичности для оценок параметров регрессии методом наименьших квадратов и проверки статистических гипотез.
- •Признаки гетероскедастичности и ее диагностирование. Обнаружение гетероскедастичности
- •1. Графический анализ остатков
- •2. Тест ранговой корреляции Спирмена
- •3. Тест Голдфелда-Квандта
- •Оценивание коэффициентов множественной линейной регрессии в условиях гетероскедастичности. Обобщенный метод наименьших квадратов.
- •Автокорреляция. Причины автокорреляции.
- •Влияние автокорреляции на свойства оценок мнк.
- •Тест серий. Статистика Дарбина – Уотсона.
- •Способы противодействия автокорреляции.
- •Стохастические объясняющие переменные. Последствия ошибок измерения.
- •Инструментальные переменные.
- •Лаговые переменные и экономические зависимости между разновременными значениями переменных.
- •Модели с распределенными лагами.
- •Модели авторегрессии как эквивалентное представление моделей с распределенными лагами.
- •Ожидания экономических агентов и лаговые переменные в моделях
- •Модели наивных и адаптивных ожиданий.
- •Модель гиперинфляции Кейгана.
- •44. Модель гиперинфляции Кейгана
- •Понятие об одновременных уравнениях. Структурная и приведенная форма модели.
- •Структурная и приведённая форма. Идентифицируемость
- •Примеры
- •Проблема идентификации. Неидентифицируемость и сверхидентифицированность.
- •Оценивание системы одновременных уравнений. Косвенный и двухшаговый мнк.
- •Системы эконометрических уравнений с лаговыми переменными.
- •Модель Кейнса.
- •Модель Клейна.
- •Матричная форма записи модели Клейна
Модель Кейнса.
Наиболее широко системы эконометрических уравнений используются для построения макроэкономических моделей функционирования той или иной страны. Большинство из них представляют собой мультипликаторные модели кейнсианского типа с той ил иной мерой сложности.
Пример: статистическая модель Кейнса для описания народного хозяйства страны в простом варианте имеет следующий вид:

где С – личное потребление в постоянных ценах,
у – национальный доход в постоянных ценах;
I – инвестиции;
- случайная величина.
В силу наличия тождества в модели (второе уравнение системы) структурный коэффициент b не может быть больше 1. Он характеризует предельную склонность к потреблению. Если он равен 0,65, то из каждой дополнительной тысячи дохода на потребление расходуется в среднем 650 руб., и 350руб. инвестируется, т.е. С и у выражены в тыс.руб. Если b>1, то y<C+I, т.е. на потребление расходуются не только доходы, но и сбережения.
Параметр Кейнс истолковал как прирост потребления за счет др. факторов. Т.к. прирост во времени может быть не только положительным, но и отрицательным, то такой вывод возможен. Однако суждение о том, что параметр характеризует конкретный уровень потребления, обусловленный влиянием др. факторов, неправильно.
Структурный коэффициент b используется для расчета мультипликаторов. По данной функции потребления можно опр-ть 2 мультипликатора – инвестиционный мультипликатор потребления Mc и инвестиционный мультипликатор национального дохода – .
Пример: 1) эта величина означает, что дополнительные вложения в размере 1 тыс.руб. приведут при прочих равных условиях к дополнительному увеличению потребления на 1,857 тыс.руб. 2) доп.инвестиции в размере 1 тыс.руб. на длительный срок приведут при прочих равных условиях к дополнительному национальному доходу в 2,857 тыс.руб.
Модель Кейнса точно идентифицируема, и для получения величины структурного коэффициента bиспользуется КМНК.
В более поздних исследованиях статистическая модель Кейнса включала уже не только функцию потребления, но и функцию сбережений r:
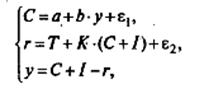
Модель Клейна.
Модель Клейна – это динамическая модель макроэкономики. Предложил ее Клейн в 1950 г. и она описывает связи между следующими показателями:
![]() ‑
потребление,
‑
потребление,
![]() ‑
инвестиции,
‑
инвестиции,
![]() ‑
заработные платы в частном секторе,
‑
заработные платы в частном секторе,
![]() ‑
заработные платы в государственном
секторе,
‑
заработные платы в государственном
секторе,
![]() ‑
совокупный спрос,
‑
совокупный спрос,
![]() -
государственные расходы,
-
государственные расходы,
![]() - доход частного капитала,
- доход частного капитала,
![]() -
капиталовложения,
-
капиталовложения,
![]() - непрямые налоги и чистый доход от
экспорта,
- непрямые налоги и чистый доход от
экспорта,
![]() - временной тренд. Единица измерения :
денежные единицы индексировались по
отношению к начальному году
- временной тренд. Единица измерения :
денежные единицы индексировались по
отношению к начальному году
![]()
Модель Клейна записывается в следующем виде
=![]()
=![]()
![]() =
=![]()
=![]()
![]() =
=![]()
=![]()
Первое уравнение
отражает зависимость потребления
от постоянной составляющей
![]() ,
от
,
,
от
,
![]() дохода частного капитала в текущем и
предыдущем году,
‑
заработной платы в государственном
секторе и
‑
заработной платы в частном секторе, и
от случайного возмущения
дохода частного капитала в текущем и
предыдущем году,
‑
заработной платы в государственном
секторе и
‑
заработной платы в частном секторе, и
от случайного возмущения
![]() .
.
Второе уравнение
отражает зависимость
‑
инвестиций от постоянной составляющей
![]() ,
от
,
дохода частного капитала в текущем и
предыдущем году, от
,
от
,
дохода частного капитала в текущем и
предыдущем году, от
![]() -
капиталовложения в предыдущем году и
от случайного возмущения
-
капиталовложения в предыдущем году и
от случайного возмущения
![]() .
.
Третье уравнение
отражает зависимость
‑
заработной платы в частном секторе от
постоянной составляющей
![]() ,
от
‑
совокупного спроса в текущем и
предыдущем году, от
- временного тренда и от случайного
возмущения
.
,
от
‑
совокупного спроса в текущем и
предыдущем году, от
- временного тренда и от случайного
возмущения
.
Последние три уравнения представляют уравнения равновесия.
Четвертое уравнение: совокупный спрос равен потреблению, плюс инвестиции, плюс государственные расходы.
Пятое уравнение: доходная часть капитала равна совокупному спросу, минус налоги, минус доход от эксплуатации..
Шестое уравнение : капитал равен капиталу предыдущего года , плюс инвестиции .
Их наличие позволяет свести систему 6 уравнений к системе 3 уравнений. Запишем вышеприведенную систему в матричной форме, представленной в таблице 1.
Решим поставленную задачу в два приема с использованием двух шагового метода наименьших квадратов (ДМНК)
Первый шаг. Приведем структурную форму записи к приведенной, т.е. установим зависимость эндогенных переменных только от экзогенных переменных. В общем виде эту процедуру запишем следующим образом:
![]()
![]()
![]()
Условие идентифицируемости выполняется:
![]() ,
где
,
где
![]() - количество
уравнений в приведенной форме, (
- количество
уравнений в приведенной форме, (![]() ),
),
![]() -
количество независимых переменных, (
-
количество независимых переменных, (![]() ;
;
![]() количество
уравнений.
количество
уравнений.
Второй шаг. Построим прогнозные значения
![]() ,
,
![]() ,
,
![]() ,
,
условно представим,
что
![]() - это х1, х2, х3 и т.д., тогда
- это х1, х2, х3 и т.д., тогда
![]() ,
,
![]() и
и
![]() .
.
Найдем произведение
матриц
![]() будет
иметь следующий вид:
будет
иметь следующий вид:
 .
.
Обратная матрица
![]() равна:
равна:
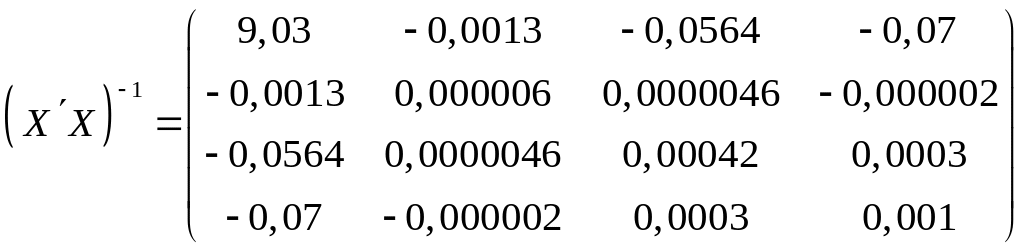 .
.
Вычислим следующие векторы:
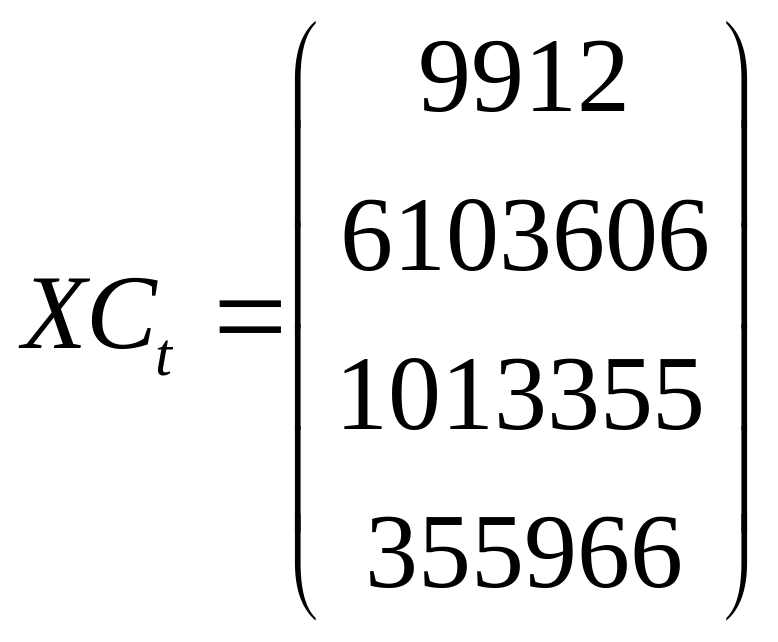 ;
;  ;
; 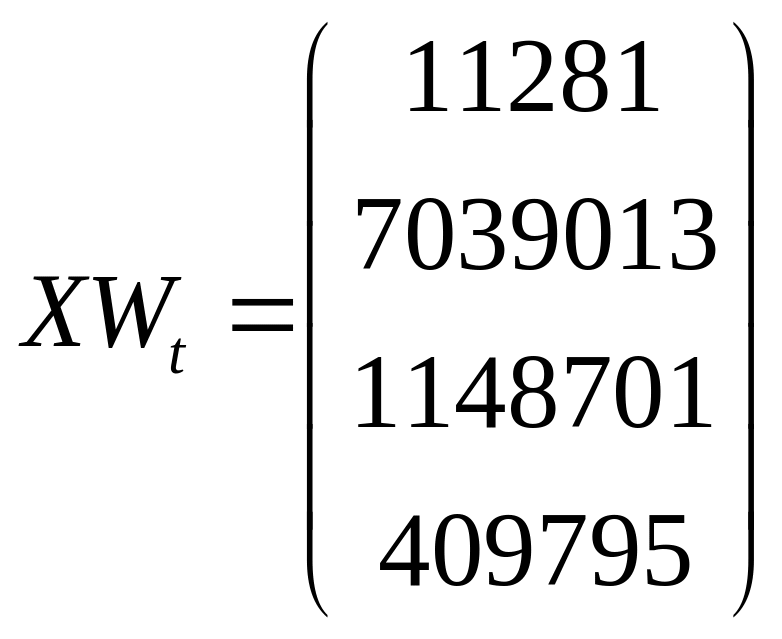
Теперь рассчитаем
![]() ,
,
![]() и
и
![]() :
:
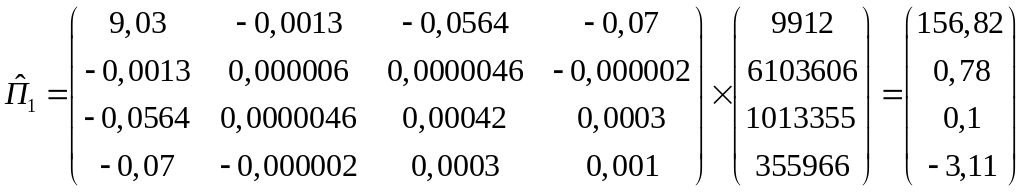
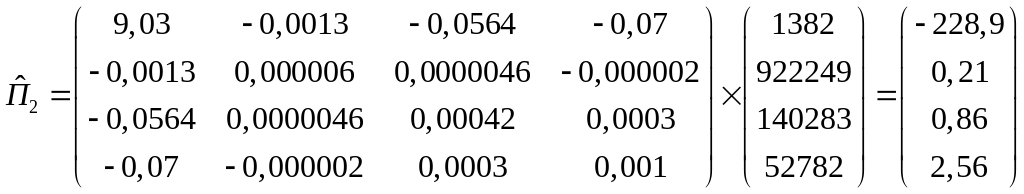
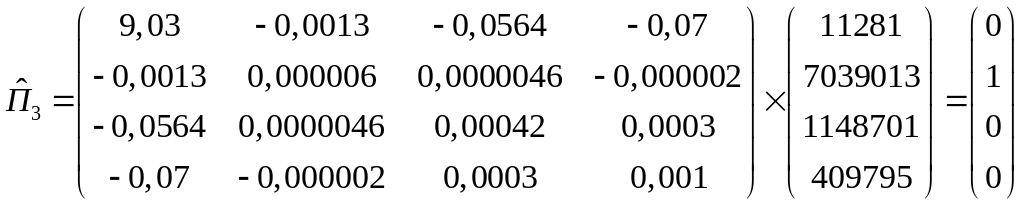
Итак, прогнозные значения будут выглядеть следующим образом:
![]() ,
,
![]() ,
,
![]() .
.
Вывод:
Таким образом, выделив из системы, состоящей из шести уравнений по модели Клейна, три уравнения по функциям потребления, инвестиций и заработной платы, получаем значения коэффициентов системы:
,
,
.
Полученные данные изобразим графически на рисунке 1.
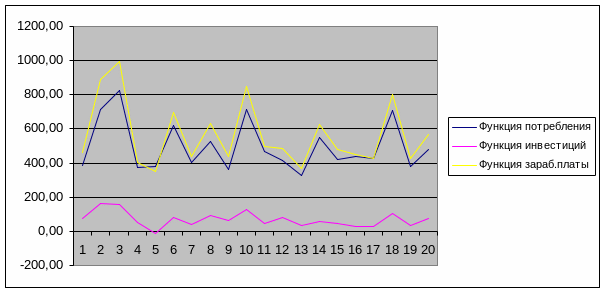
Рисунок 1. – График модели из трех уравнений: функция потребления, инвестиций и заработной платы за 4 года.
Из полученных данных видно, что наибольший подъем был в начале 2000 года, когда потребление достигало отметки 1000 тыс.грн., инвестиции – 800 тыс.грн., а налоги немного не доходили до 200 тыс.грн. Самые низкие показатели по этим трем функциям приходились на начало 2003 года. Во втором квартале 2004 года снова наблюдается подъем, а в третьем квартале этого же года – значительный спад.
