2. Тест ранговой корреляции Спирмена

Значения и (абсолютные величины) ранжируются (упорядочиваются по величинам). Затем определяется коэффициент ранговой корреляции:

(4.1)

где – разность между рангами и , ; – число наблюдений.

Например, если является 25-ым по величине среди всех наблюдений, а является 32-м, то .

Затем рассчитывается статистика:

(4.2)

Если значение, рассчитанное по формуле (4.2), превышает критическое (определяемое по приложению 1), то необходимо отклонить гипотезу об отсутствии гетероскедастичности. В противном случае гипотеза об отсутствии гетероскедастичности принимается.

Если в модели регрессии больше, чем одна объясняющая переменная, то проверка гипотезы может осуществляться с помощью -статистики для каждой из них отдельно.

3. Тест Голдфелда-Квандта

В данном случае предполагается, что стандартное отклонение пропорционально значению переменной в этом наблюдении, т.е. , .

Тест Голдфелда-Квандта состоит в следующем:

1. Все наблюдений упорядочиваются по величине .

2. Вся упорядоченная выборка после этого разбивается на три подвыборки размерностей соответственно.

3. Оцениваются отдельные регрессии для первой подвыборки ( первых наблюдений) и для третьей подвыборки ( последних наблюдений). Для парной регрессии Голдфелд и Квандт предлагают следующие пропорции: ; . Если предположение о пропорциональности дисперсий отклонений значениям верно, то дисперсия регрессии по первой подвыборке (рассчитываемая как 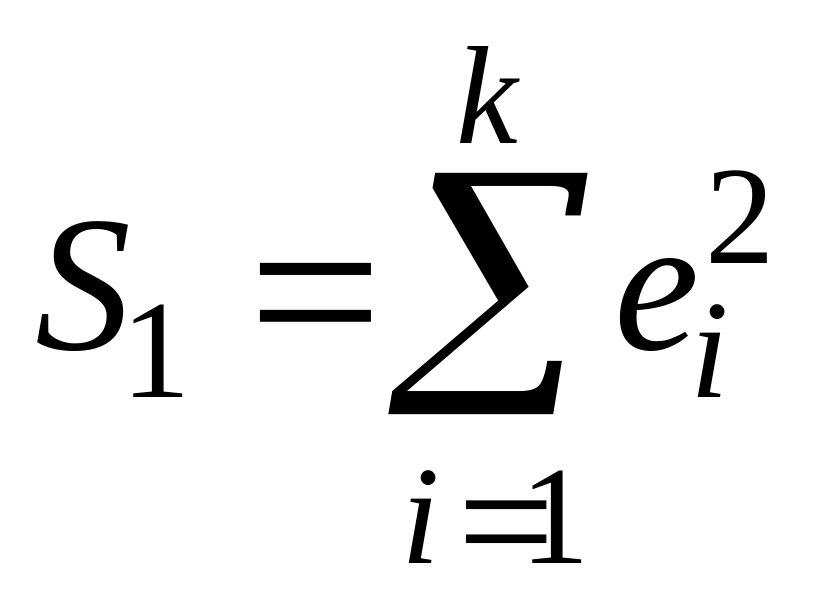) будет существенно меньше дисперсии регрессии по третьей подвыборке (рассчитываемой как ).

4. Для сравнения соответствующих дисперсий строится соответствующая -статистика:

(4.3)

Здесь – число степеней свободы соответствующих выборочных дисперсий ( – количество объясняющих переменных в уравнении регрессии).

Построенная -статистика имеет распределение Фишера с числом степеней свободы .

5. Если (где , определяется из приложения 2, – выбранный уровень значимости), то гипотеза об отсутствии гетероскедастичности отклоняется.

Этот же тест может использоваться при предположении об обратной пропорциональности между и значениями объясняющей переменной. При этом статистика Фишера имеет вид:

(4.4)

Для множественной регрессии данный тест обычно проводится для той объясняющей переменной, которая в наибольшей степени связана с . При этом должно быть больше, чем . Если нет уверенности относительно выбора переменной , то данный тест может осуществляться для каждой из объясняющих переменных.

32. Оценивание коэффициентов множественной линейной регрессии в условиях гетероскедастичности. Обобщенный метод наименьших квадратов.

Обобщенный метод наименьших квадратов.

При нарушении гомоскедастичности и наличии автокорреляции ошибок рекомендуется заменять традиционный метод наименьших квадратов (OLS) обобщенным методом (GLS).

Обобщенный метод наименьших квадратов применяется к преобразованным данным и позволяет получить оценки, которые обладают не только свойством несмещенности, но и имеют меньшие выборочные дисперсии.

Предположим, что среднее значение остатков равно нулю, а дисперсия их пропорциональна величине , т.е.

, где - дисперсия ошибки при конкретном i-м значении фактора; - постоянная дисперсия ошибки при соблюдении предпосылки о гомоскедастичности остатков; - коэффициент пропорциональности.

При этом предполагается, что неизвестна, а в отношении величины K выдвигается гипотезы, характеризующие структуру гетероскедастичности.

В общем виде для уравнения y = a + b  x +  модель примет вид:

В данной модели остаточные величины гетероскедастичны. Предположив в них отсутствие автокорреляции, перейдем к уравнению с гомоскедастичными остатками, поделив все переменные, зафиксированные в ходе i-го наблюдения, на . Тогда дисперсия остатков будет величиной постоянной, т.е. = . Иными словами, от регрессии y по x мы перейдем к регрессии на новых переменных: .

Дальнейшее преобразование уравнения регрессии и затем системы нормальных уравнений, то получим коэффициент регрессии:

.

При обычном применении метода наименьших квадратов к уравнению линейной регрессии для переменных в отклонениях от средних уровней коэффициент регрессии b определяется по формуле

Как видим, при использовании обобщенного МНК с целью корректировки гетероскедастичности коэффициент регрессии b представляет собой взвешенную величину по отношению к обычному методу наименьших квадратов 1/K.