Вопрос 4. Теорема о необходимом условии дифференцируемости функции. Следствие (связь с градиентом)

Теорема (необходимое условие дифференцируемости функции). Пусть дифференцируема в , тогда в этой точке существуют все частные производные и они равны соответственно координатам , обратное утверждение в общем случае не верно. Доказательство. Пусть дифференцируема в . , полагая . , тогда . Следствие (связь с градиентом). Пусть дифференцируема в , тогда .

в

f(x,y)=

опрос5 Пример функции, имеющей частные производные, но не дифференцируемой в точке.

, x²+y²≠0

0, x²+y²=0

Очевидно, что и . Но эта функция не дифф-ма по совокупности в т (0;0). Если бы она была дифф-ма, то ее приращ-е в этой точке можно было бы записать как Δf(0,0) = 0*Δx + 0*Δy + α(Δx, Δy) Δx + β(Δx, Δy) Δy = α(Δx, Δy) Δx + β(Δx, Δy) Δy, (где α(Δx, Δy) и β(Δx, Δy) стремятся к 0 когда 0). Однако, это не так. = + 0 = (т.к. x₀=0; y₀=0) = = + = + . Т.е. в нашем случае в роли α выступает , а в роли β - и эти выражения не определены при 0. Значит, приращ-е нашей функции в т (0;0) нельзя представить в виде, который дает дифференциируемость ф-ции в этой точке по опр-ю => эта функция в т. (0;0) не дифф-ма, хотя имеет там частные производные по обеим переменным.

(этот пример иллюстрирует невыполнение утверждения, обратного к теореме о необходимом условии дифференцируемости функции).

PS Доказательство пункта 5 мое – за правильность не ручаюсь. Подпись: Fil McArov

Достаточное условие дифф-ти ф-ции многих незавю переменных. Если имеет частные произв-е по всем переменным в окрест. точки x₀ G, причем все эти произв-е непрерывны в самой точке, то функция дифф-ма в этой точке. Док-во Для простоты док-во для 2х пер-х. Для многих – аналогично. f:(GcR²)->R; f=f(x,y); x₀=(x₀,y₀); Тогда . сгруппируем 1 и 3, 2 и 4 слагаемые, и каждую из полученных разностей рассмотрим как ф-цию одного переменного и применим трм Лагранжа в форме о конечных приращ-ях. получаем, что существуют такие действит-е ξ из (x₀; x₀+Δx) и η из (y₀; y₀+Δy), что Δf(x₀) = f_x’(ξ, y₀+Δy)Δx + f_y’(x₀, η)Δy. В силу непр-ти f_x’(ξ, y₀+Δy) и f_y’(x₀, η) можно записать: f_x’(ξ, y₀+Δy) = f_х’(x₀, y₀) + α(Δx, Δy), где

α(Δx,Δy)->0 при Δx–>0,Δy–>0, и f_y’(x₀, η) = f_y’(x₀, y₀) + β(Δx,Δy), где β->0, Δx–>0,Δy–>0. Подставим: f_х’(x₀, y₀)Δx + f_y’(x₀, y₀)Δy + α(Δx,Δy) + β(Δx,Δy) => ф-ция здесь дифф-ма по определению.

Трм. о производной сложной ф-ции. Если вып-ся 1)x_i = x_i(t_1...t_m), i=1...k и ф-ция дифф-ма в t₀ из R^m. 2) f(x₁...x_k) дифф-ма в x₀ из G c R^k, то сложная ф-ция f(x(t)) дифф-ма в t₀ из R^m и имеет место равенство: j=1..m; Док-во: Δx_i(t₀) = B_ijΔt_j + β_ijΔt_j (β_ij->0, Δt->0) ; Δf(x₀) = A_iΔx_i + α_iΔx_i (α_i->0, Δx->0); Тогда Δf(x(t₀)) = A_i ( B_ijΔt_j + β_ijΔt_j) + α_i( B_ijΔt_j + β_ijΔt_j) = ( A_iB_ij)Δt_j + ( (A_iB_ij + B_ijα_i + α_iβ_ij)Δt_j = {полагаем c_j= A_iB_ij ; γ_j= (A_iB_ij + B_ijα_i + α_iβ_ij) } = c_jΔt_j + γ_jΔt_j и γ_j->0 при Δt->0, а это значит, что f(x(t)) дифф-ма в t₀

Определение 1го дифф-ла. Трм об инвариантности формы 1го дифф-ла. Если дифф-ма в x₀ G, т.е. ее полное приращ-е зап-ся так: Δf(x₀) = AΔx + α(Δx)*Δx, где α->0 при Δx->0. Тогда AΔx = df(x₀) = называется полным дифф-лом функции f(x) в точке x₀ из G_. А величина A_iΔx_i = di f(x₀) – частным дифф-лом в точке по перем-й x_i. Т.к. по усл-ю x₁...x_k – независ перем-е, то их приращ-я Δx₁...Δx_k равны соответственно dx₁...dx_k В силу необх-го усл-я дифф-ти ф-ции f(x) в т.x₀ имеем, что в-р A будет иметь коорд. A_i= и формулы полного и частноо дифф-ла перепишутся как 1)df(x₀) = 2) di f(x₀)= ТРМ пусть 1)x_i=x_i(t₁...t_m) – дифф-ма в т. t₀ R^m. 2)f(x) дифф-ма в соотв. x₀=x(t₀) G c R^k. Тогда форма первого дифференциала df(x(t₀)) инвариантна. df(x(t₀))= df(x₀). Док-во: df(x(t₀)) = = )= = .

Определение производной по направлению, трм о связи произв. по напр-ю и градиента. Пусть и x₀ G и пусть в R^k задано направление e, ||e||=1. Тогда lim (t->0) будем называть производной по напр-ю e в т. x_0. lim (t->0) = ; (замеч-е. из этого опр-я следует, что = lim (t->0) ) ТРМ Если дифф-ма в т. x₀ G то прозв-я от этой ф-ции по любому напр-ю в точке x₀ существует и вычисл-ся по формуле = (grad f(x₀), e). Док-во: e = (cosα₁, cosα₂ ... α_k). f(x) дифф-ма в x₀ => f(x)-f(x₀) = AΔx + α(Δx)Δx; A = gradf(x₀) = ( ) при Δx->0; тогда полагая в этой формуле x = x₀ + te, получаем, что f(x₀+te)-f(x₀) = Ate + αte. Тогда lim_Δx->0( = lim_t->0 = (A,e) = (grad(f(x₀)), e).

Угол м\у векторами в многомер. векторном простр-ве, трм о коллинеар и ортогонал вект. Опр: x лежит в R_n^k, y лежит в R^k, x = (x₁,x₂ ... x_k), y = (y₁, y₂ .. y_k); |(x,y)|≤||x||*||y||; x≠0; y≠0, 0≤ω≤Π; cosω = Тогда число ω – угол между векторами x и y. Опр2 Если существует λ≠0 такая, что x= λy, то векторы x и y называются коллинеарными, а если (x,y)=0, то векторы наз-ся ортогональными. ТРМ Пусть x и y – ненулевые из R^k. Тогда если 1) ω=0; ω= Π – вектора коллинеарны, 2) ω=Π\2 – ортогональны. Док-во 1) ω=0 –> (x,y) = ||x||*||y||; x=λy; (x- λy; x-λy) = (x,x) - 2 λ(x,y) + λ²(y,y) = ||x||² - 2λ||x||*||y|| + λ²||y||²; cos0=1 и (x- λy; x-λy)=0, тогда λ = +- ||x|| / ||y|| 2)очевидно следует из скалярного произведения.

Четыре свойства градиента функции многих переменных. Выясним смысл градиента функции многих переменных. Для этого воспользуемся формулой выч-я произв-й по напр-ю через градиент. , где ω = gradf(x₀)^e; т.о. имеем: . Свойства: 1) В направлении вектора grad f(x₀), произв-я по напр-ю принимает наибольшее значение, равное ||gradf(x₀)||, а в противоположном – наименьшее, равное -||gradf(x₀)||. эти направления называются соответственно напр-ями нискорейшего подьема и наискорю спуска функции f(x) в x_0. 2) По всем направлениям, ортогональным к напр-ю градиента, =0, а по всем напр-ям, отличным от ортогонального принимает промежуточные значения, т.е. -||gradf(x₀)||≤ ≤||gradf(x₀)||. 3) grad f(x₀), (x₀ из R) есть вектор, направленный из точки x₀ в сторону наискорейшего возрастания функции и по величине равный производной от функции f(x) в этой точке по этому направлению.

12. Частную производную n-ного порядка от ф-ции по переменным x_i1, x_i2 ,…,x_in (i=1,2,…k) определим по индукции с помощью след. соотношения:

, если все индексы совпадают (i₁,i₂,…,i_n=i), то будем обозначать: , если же не все индексы совпадают, то такую производную будем называть смешанной.

Ф-ция называется n раз дифференцируемой в точке , если все её частные производные (n-1)-ого порядка дифференцируемы в этой точке.

Теорема о равенстве смешанных производных. Пусть f(x,y)(GCR²)→R дифференцируема в любой точке из некоторой окр-ти точки (x₀y₀), целиком принадлежащей G и дважды дифф-ма в самой точке (x₀y₀), тогда смешанные производные в этой точке равны.

Доказательство. Рассмотрим частные приращения ф-ции f(xy) в точке (xy):

∆_xf(x₀y₀)=f(x₀+∆x,y₀)-f(x₀y₀) ; ∆_yf(x₀y₀)=f(x₀,y₀+∆y)-f(x₀y₀), и составим приращения от приращений: ∆_y(∆_xf(x₀y₀))=∆_xf(x₀,y₀+∆y)-∆_xf(x₀y₀)=

=f(x₀+∆x,y₀+∆y)-f(x₀,y₀+∆y)-f(x₀+∆x,y₀)+f(x₀y₀), аналогично для ∆_x(∆_yf(x₀y₀): ∆_x(∆_yf(x₀y₀))=∆_yf(x₀+∆x,y₀)-∆_yf(x₀y₀)=

=f(x₀+∆x,y₀+∆y)-f(x₀+∆x,y₀)-f(x₀,y₀+∆y)+f(x₀y₀).

В силу дифференцируемости f′(xy) в точке (x₀y₀) получим, что

∆_y(∆_xf′(x₀y₀))=(f′_x(x₀,y₀+∆y)-f′_x(x₀y₀))∆x=(f′′_xy(x₀y₀)∆y+β₁(∆y)∆y)∆x=(f′′_xy(x₀y₀)+β₁(∆y))∆y∆x где β₁(∆y)→0, при ∆y→0, аналогично получим, что:

∆_yf(xy)=f′_y(xy)∆y+α₁(∆y)∆y, ∆_x∆_yf(x₀y₀)=(f″_yx(x₀y₀)+α₂(∆x))∆x∆y (α₁(∆x)→0 при ∆x→0)

т.к. ∆_x∆_yf(x₀y₀)=∆_y∆_xf(x₀y₀), то f′′_xy(x₀y₀)+β₁(∆y)=f″_yx(x₀y₀)+α₂(∆x)), переходя к пределу при ∆x→0 ∆y→0 в последнем равенстве, мы получаем равенство смешанных производных.

13. Пусть дана симметричная квадратная матрица КхК: , тогда ф-ция называется квадратичной формой, порожденной симметрической матрицей А Вычислим: В силу симметричности имеем

Лемма о представлении квадратичной формы. Если коэффициенты квадр. формы (1)удовлетворяют условию a_ij=a_i*a_j , то она представима в виде полного квадрата суммы

Доказательство. Методом мат. индукции при к=2 (1)=a²₁x²₁+a₁a₂x₁x₂+a₂a₁x₂x₁+a²₂x²₂=(a₁x₁+a₂x₂)²

Предположим, что верно для к>2, проверим для к+1:

14. Пусть ф-ция f:(GCR^k)→R (n-1) раз дифференцируема некоторой окрестности S(εx^→₀) и n раз дифференцируема в самой точке x^→₀, тогда дифференциал n-ного порядка

Определим дифференциальный оператор по формуле

Произведением операторов и назовём оператор ; Линейной комбинацией операторов и назовём оператор, действующий по следующей формуле: (aD_ij…p+bD_rs…q)f=aD_ij…pf+bD_rs…qf

Теорема о представлении второго дифференциала ф-ции нескольких независимых переменных Пусть f:(GCR^k)→R Пусть d²f(x^→)определен в точке x^→₀, то он может быть вычислен по формуле:

Доказательство. ∆x_i=dx_i т.к x независимая переменная

Последнее выражение в формуле есть квадратичная форма

, учитывая, что для дважды дифференцируемой ф-ции выполнено равенство смешанных производных, а также воспользовавшись леммой о представлении квадратичной формы, получим

Теорема о нарушении формы n-ного дифф-ла. n≥2 При n≥2 форма n-ного дифф-ла зависит от того, являются ли x_i (i=1..k) независим. переменными или n раз дифференциируемыми функциями от своих переменных. Д-во: Докажем, что форма нарушится для n=2 и этого достаточно для док-ва всей трм. Пусть x_i (i=1..k) – дважды дифф-е функции. тогда d²x_i вообще говоря не равны нулю и форма второго дифф-ла такова: d²f(x) = d(df(x))= = . Но здесь d(dx_i)=d²x_i≠0, а первое слагаемое представляет из себя второй дифф-л f(x) когда x_i-незав.перем-е. Таким образом видно, что форма уже второго дифф-ла нарушается => нарушается и форма более высоких дифф-лов. Трм.доказ.

№16.

Определение:

Пусть f(x) = f(x₁, x₂… x_k): (GR^k)R, тогда f(x) наз.

1. Возрастающей (убывающей) в направлении l на отрезке в области G, коллинеарном с l, если для любых точек x₁, x₂, лежащих на этом отрезке и таких, что x₂ следует за x₁ в направлении l, выполняется f(x₂)>f(x₁) (f(x₂)<f(x₁))

2. Возрастающей (убывающей) в т.x_G в направлении l, если можно указать отрезок в G, коллинеарном l, с началом в т. x_ и такой, что f(x) возрастает (убывает) на этом отрезке в направлении l.

Теорема.

О монотонности и знакопостоянстве функции.

f:(GR^k)R – диф-мая в G, тогда

1. Если во всех точках отрезка G и коллинеарного с l производная по напрвлению , то функция f(x) – возрастает на этом отрезке в направлении l

2. Если во всех точках отрезка G и коллинеарного с l производная по напрвлению , то функция f(x) - убывает на этом отрезке в направлении l

3. Если во всех точках области G , то f(x)=const

Доказательство:

1) , x₁, x₂ отрезку, x₂ следует за x₁ в направлении l, 0t1

F(t)=f(x₁+t(x₂-x₁))=f(x₁+tl||x₂-x₁||,

F(t) на сегменте [0;1] удовлетворяет всем условиям т. Лагранжа: F(t) – непрерывна как сложная функция;

t(0,1)

По т. Лагранжа (0,1): f(x₂)-f(x₁)=F(1)-F(0)=F’_t()(1-0)=F’_t()=

Т.к. оба множителя положительны, значит, f(x₂)>f(x₁)

2)доказывается аналогично

3)если x₁, x₂G можно соединить отрезком, целиком принадлежащим G, то

(т.к. первый множитель равен 0), значит, f(x₁)=f(x₂)

Соединим их ломаной линией G, в вершинах ломаной значения равны, значит, функция постоянная.

№17.

Теорема Тейлора.

S(,x_)=(xR^k, ||x- x_||<) -  окрестность т. x_ в R^k

f: S(,x_)R и является (m+1) раз диф-мой функцией в этой окрестности, тогда (1), S(,x_)

Доказательство:

x такое, что т.x_+xS(,x_) и соединяет x_ и x_+x отрезком x=x_+tx, 0t1

F(t)=f(x_+tx), тогда

F(1)-F(0)=f(x_+tx)-f(x_)=f(x_)

По условию f(x) (m+1) раз диф-мая функция  F(t) удовлетворяет всем условиям т. Тейлора для функции одного переменного, т.к.

существует при 0t1, тогда для неё можно записать формулу Тейлора в окрестности t_[0,1]

(2)

 между t и t_

Т.к. t – независимая переменная, то

t=1, t_=0

(2)

В силу инвариантности формы n – ого диф-ала при линейной замене мы получаем

, =x_+x

dt=t=1-0=1

x_i=x_i+tx_i

dx_i=x

Подставляя это в (2), мы получаем окончательную формулу.

18.Определение экстремума вещественнозначной функции. Теорема о необходимости условия экстремума.

Def.1.:Пусть (X,d) – метрическое пространство, и f:(EX)R, тогда

1)будем говорить, что функция f имеет локальный минимум в точке E, если

2)будем говорить, что функция f имеет локальный максимум в точке E, если

Трм.1.:(Необходимое условие экстремума)

Пусть f:(GR^k)R и имеет локальный минимум/максимум в точке G, а также дифференцируема в этой точке. Тогда необходимо выполняются следующие условия:

1) , где – любое направление в R^k;

2)grad(f( ))=0

3) , где

4)

Док-во: 1)Пусть f(x) – дифференцируема в точке Gв этой точке существует .

Предположим, для определённости пусть f имеет в точке локальный минимум. (1). Тогда для достаточно малых вещественных значений tR точка (окрестности ). Тогда по определению производной по направлению имеем:

, ч.т.д.

2)Т.к. , а  из того, что - единичный вектор



3)Т.к. координаты вектора координаты вектора градиента равны

нулю, а эти координаты есть частные производные по всем направлениям  .

4)Т.к.

Эквивалентность всех этих четырёх определений очевидна.

19.Определение положительно и отрицательно определённой квадратичной формы. Критерий Сильвестра. Лемма о знакопеременной квадратичной форме.

Def. 1.:Квадратичная форма называется

1)положительно определённой, если .

2)отрицательно определённой, если .

3)знакопеременной, если , что , и

Трм. 1.:(Критерий Сильвестра знакоопределённости квадратичной формы)

Пусть - симметричная квадратная матрица размерности k*k, порождающая квадратичную форму и A₁=a₁₁, , … , - главные окаймляющие миноры матрицы. Тогда, для того, чтобы была положительно/отрицательно определённой, необходимо и достаточно, чтобы A₁>0, A₂>0,…,A_k>0 / A₁<0, A₂>0,…,sgn(A_k)=(-1)^k. (WITHOUT PROVE!)

Лемма 1.:(Оценки знакоопределённости квадратичной формы)

Если положительно определена, то  , если отрицательно определена  .

Док-во: 1)Пусть положительно определена, и - единичный вектор из R^k, т.е.

. Но тогда есть непрерывная функция относительно переменных e₁,e₂,…,e_k, определённая на сфере . Поскольку эта сфера есть замкнутое и ограниченное множество, то в силу второй теоремы Вейерштрассе функция достигает своей точной верхней и нижней границ на сфере: . Но тогда для . Вернёмся: .

2) Док-во мое: все то же, но: . (берем –M, т.к. M>0 ) Но тогда для . Вернёмся: .

Замечание: Если , то во всех нер-вах будет просто равенство

20. Теорема о достаточном условии экстремума функции многих переменных.

Трм. 1.:(Достаточное условие экстремума)

Пусть - дважды дифференцируемая функция в некоторой , и x₀ – точка возможного экстремума функции, а также в этой точке функция имеет непрерывные вторые производные. Тогда:

1)Если представляет собой положительно определённую квадратичную форму от дифференциалов независимых переменных , то функция имеет локальный минимум в x₀.

2)Если представляет собой отрицательно определённую квадратичную форму от дифференциалов независимых переменных, то функция имеет локальный максимум в x₀.

3) Если представляет собой знакоопределённую квадратичную форму, то x₀ не является экстремумом.

Замечание: Т.к. дважды дифференцируема в , то для неё справедлива

формула Тейлора для случая, когда m=1; (1), при этом при . А т.к. частные производные (где при ) и т.к. - точка возможного экстремума, а функция дважды дифференцируема, то df(x₀)=0 и равенство (1) перепишется в виде: 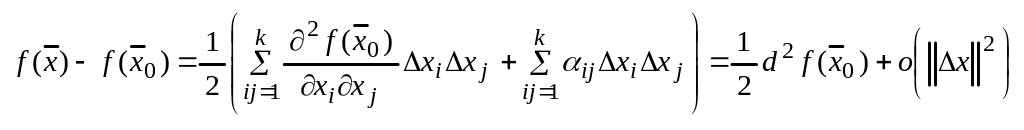(принимая, что )

Док-во: 1)Если положительно определённая квадратичная форма от , то

согласно лемме 1 , где m>0. Таким образом,

, и для достаточно малых ||x||<<1 эта разность

больше нуля, значит это точка локального минимума.

2)Если - отрицательно определённая квадратичная форма,  (по лемме 1)

, M>0, тогда

 точка локального

максимума.

3)Пусть - приращение аргумента x в точке - при котором квадратичная форма (2), а - приращение в , при котором

(3).

Тогда из (2) можно сказать, что , то . Будем уменьшать , чтобы направление вектора сохранилось  для таких , уменьшающихся по норме, (4).

Аналогично рассмотрим случай (3) и получим, что (5). Тогда получаем, что для , , одновременно выполняется неравенства (4) и (5)  локального экстремума нет!!!!!!

21.Определение неявной функции одного переменного. Теорема о существовании неявной функции одного переменного.

Def. 1.:Функция y=f(x), заданная уравнением F(x,y)=0, где (x,y)GR^k называется неявной функцией.

Трм. 1.:(О существовании неявной функции одного переменного)

Пусть GR^k – область плоскости R² (открытое связное множество) и функция F(x,y):GR. Тогда если выполняются условия:

1)F(x,y)C_(G)

2)F(x₀,y₀)=0, где x₀,y₀ – некоторые фиксированные точки области G.

3)При фиксированном x, как функция переменной, y монотонно возрастает/убывает;

тогда уравнение F(x,y)=0:

1)в некоторой окрестности определяет функцию как однозначную функцию от x;

2)f(x₀)=y₀;

3)y=f(x) непрерывна для .

Док-во: Т.к. G – открытое множество, а M₀ – его внутренняя точка, то её можно

Окружить прямоугольником, целиком G.

Зафиксируем x=x₀ и будем перемещаться по прямой A₀B₀. Тогда F(x,y) в силу монотонности будет F(B₀)>0, B₀(x₀,y₀+`) и F(A<sub>0</sub>)<0, A<sub>0</sub>(x<sub>0</sub>,y<sub>0</sub>-`). Проведём горизонтальные прямые через точки A₀,B₀: B₁B₂ и A₁A₂. На этих прямых определены две функции переменной x: F(x₀,y₀-`) и F(x<sub>0</sub>,y<sub>0</sub>+`). По условию теоремы они непрерывны по x   окрестность (x₀-,x₀+), где 0<₀<, где обе функции сохраняют знак.

Зафиксируем теперь x из окрестности - - и рассмотрим функцию F(x,y) на отрезке . Т.к. F(x,y) непрерывна по y на [y₀-`,y<sub>0</sub>+`] n принимает в и значения разных знаков  по первой теореме Коши для непрерывных функций такое, что и в силу монотонности F(x,y) по y, эта точка – единственная. Т.о.  однозначная функция y=f(x)!!!

Теперь докажем, что неявная функция y=f(x) непрерывна в любой точке из

интервала x(x₀-,x₀+). Т.к. для любой точки из этого интервала выполнены те же условия, что и для x₀  достаточно доказать непрерывность в x_0. В силу произвольности `, возьмём `=, а =()=₀. Тогда для всех |x-x₀|<??? Видно, что |f(x)-f(x₀)|<`=.

22. Теорема о дифференцируемости неявной функции)

Трм. 1.:(О существовании производной неявной функции)

Пусть F(x,y):(G R²)R удовлетворяет условиям:

1)F(x,y) =0 – дифференцируема в области G.

2) непрерывна в области G (по совокупности)

3) , где (x₀,y₀)G,

Тогда выполняются все утверждения теоремы существовании непрерывности неявной функции, и кроме того y=f(x) – дифференцируема в S(,M₀)G, M₀(x₀,y₀).

Док-во: Т.к. частная производная по y непрерывна в точке (x₀,y₀) и неравна в этой точке 0, то S(,M₀)G, в которой и принимает определённый знак  функция

F(x,y) монотонна по y. Но тогда выполняются все условия трм. 1. (О

существовании непрерывной неявной функции). Для доказательства

дифференцируемости функции y=f(x) придадим приращение x аргументу x. В

силу непрерывности бесконечно малое приращение x будет соответствовать бесконечно малому y. При этом (x+x,y+y)S(,M₀). В силу условий дифференцируемости точка (x+x,y+y) будет удовлетворять пункту 1, т.е. при подстановке тоже будет давать 0. Найдём F(x,y):



, (1) при этом , т.к. и не зависит от x. Выберем x достаточно малым, чтобы β0.

Перейдём в (1) к пределу при x0:

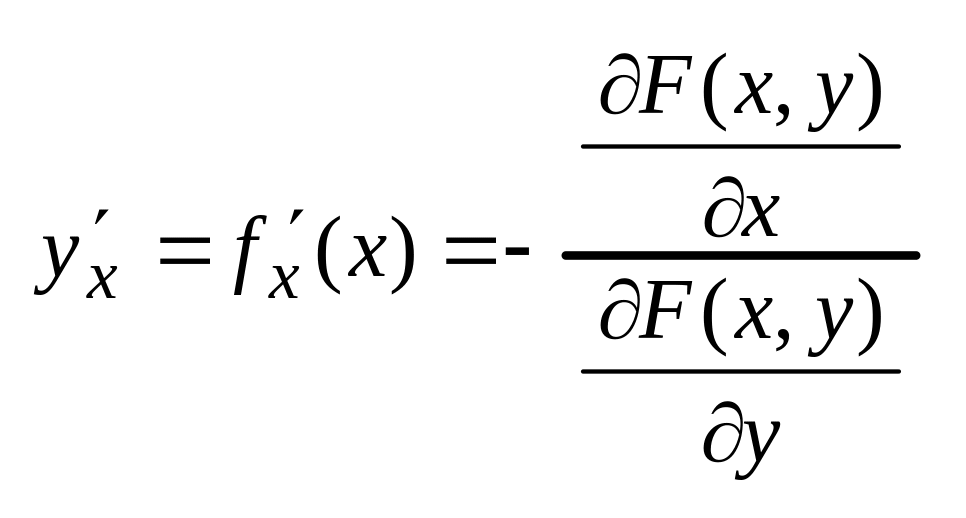
 функция дифференцируема в некоторой области G  дифференцируема и в точке x₀, ч.т.д.

Определение неявной функции многих переменных. Теорема о существовании непрерывности и дифференцируемости неявной функции многих переменных.

Опред: Функция y=f(x1,x2…xk) заданная уравнением F(x;y), где (x,y)  G  Rk*R=Rk+1 называется неявной функцией к – переменных.

Теор (О существовании непрерывной и дифференцируемой неявной функции многих переменных)

Пусть G  Rk+1 F(x;y):GR и удовлетворяет :

F(x;y)=0 дифференцируема в области G

2. ∂F(x;y)/∂y – непрерывна в области G

в точке х0 ∂F(x0;y0)/∂y  0 (x0;y0)  G

F(x0;y0)0

Тогда  окрестность S ( , M0), M0(x0,y0)=M0(x10, x20…xk0, y0)  G

В этой окрестности уравнение F(x;y)=0 определяет однозначную непрерывную неявную функцию к- переменных.

F(x;y)=0 y=f(x)=f(x1,x2…xk)

y=f(x0)

y=f(x) дифференцируема в окрестности S ( , M0) по всем переменным

определение функциональных определителей

опред: Пусть даны n-функций от n-переменных yi=fi(x1,x2…xn) y=1…n которые определены в некоторой области G из Rn и имеют в этой области частные производные по всем переменным тогда определитель:

называется функциональным определителем (определителем Якоби) или якобианом

Теор(Теорема об умножении якобианов)

Пусть xi=xi(t) i=1…n – дифференцируемые функции в точке t0Rn и функции yi=yi(x) i=1…n дифференцируемые функции в точке x0=x(t0). Тогда якобиан системы сложных функций yi=yi(x(t)) i=1…n может быть вычислен по следующей формуле:

D(y)/D(t)=D(y)/D(x)*D(x)D(t)

Док-во: Используя правило умножения определителей кводратных матриц An*n и Bn*n det An*n n0 det Bn*n n0 det(A*B)=det(A)*det(B) получаем

D(y)/D(x)*D(x)D(t)= * =

=

Если система дифференциальных функций yi=fi(x1,x2…xn) y=1…n Разрешена относительно x1 x2…xn и они тоже дифференцируемы тогда функциональные определитель

D(y)/D(x)*D(x)D(t)=1

D(y)D(y)=

Определение системы неявных функций. Терема о существовании непрерывной и дифференцируемой системы неявных функций

Опред: yi=fi(x) i=1…m x  Rk заданная системой уравнений F(x, y1, y2,…ym)=0; j=1…n, (x,y)G Rk*Rm=Rk+m Называется системой неявных функций многих переменных

Теорема (о существовании системы неявных функций)

Пусть Fi(x,y)(i=1…m) : (GRk*Rm)R и удовлетворяет условиям:

F(x,y)- дифференцируема в G

∂Fi(x,y)/∂y ij=1…m – непрерывны в G

∂Fi(x0,y0)/∂yj0

Fi(x0,y0)0

Тогда  S(, M0) M0(x0,y0) G что в пределах этой окрестности

Fj(x,y)=0;

j =1…m (2)

Система (2) определяет единственность однозначной функции

fj(x0)=y0j y0=(y01, y02…y0m) j=1…m

yj=fj(x1, x2…xm) j=1…m

Непрерывна и дифференцируема в этой окрестности S(, M0)

Определение условного экстремума . Два способа отыскание условного экстремума

Опед Пусть f:(G Rn+m )R (n+m) зависит от x1,x2…xn+m которые получены

Уравнением связи Фj(x1,x2…xn+m)=0 и j=1…m (1)

Тогда будем говорить что в точке x0=(x10, x20…xn0, xn+10…xn+m) удовлетворяющей уравнению связи (1) Функция y=f(x) имеет условный или относительный минимум если :

(0)(xG, Фj(x)=0 (j=1…m), x-x0):f(x)f(x0)

аналогично условный максимум если

f(x)<=f(x0)

два способа нахождения условного экстремума

1-ый (Способ подстановки)

Предположим что в области G якобиан D(Фj)/D(xn+1, xn+2…xm+m)0

Тогда из системы (1) однозначно находятся функции:

xn+1=1(x1,x2…xn)

xn+2=2(x1,x2…xn)

……………………  дважды диффреренцируемы

xn+m=m(x1,x2…xn)

Подставим y=f(x1,x2..xn, 1(x1,x2…xn), 2(x1,x2…xn)… m(x1,x2…xn) )= =f*(x1,x2…xn) – Функция от n независимых переменных. Исследуем эту функцию на обычный и безусловный экстремум и находим точки

M0(x10,x20…xn0) и тогда в точке M*0(x10, x20, 10, 20…m0) мы имеем условный минимум нашей функции.

2-ой (Способ неопределённых множителей Лагранжа)

Функция L=f(x)+ (x) которая зависит от n+m независимых переменных и m постоянных множителей.

y=f(x) x Rk+m

Фj(x1,x2…xn+m)=0

j=1…m  система (1)

Используя необходимое условие экстремума и уравнение связи (1) из системы уравнений

L(x,) = 0 (j=1..n+m)

Фj=0 (j=1..m)

Находим подозрительные точки M*0(x10, x20, 10, 20…m0) 

(*)

При условии что выполняется (1)

∂Фj(x)=0 и j=1..m  вирызить m значений dxn…dxn+k dx…dxn

и подставить из в (*) Если положительно определена то минимум если отрицательно то максимум