5. Аппроксимация функций. Линейная и квадратичная интерполяции.

Пусть y явл. ф-й от х. Известны лишь некоторые значения , т.е дискретному множеству поставлено в соотв. дискретное множество – функция задана таблично. Ставится задача отыскания значения ф-и y в других точках, отличных от узлов . Этой цели и служит задача о приближении или аппроксимации ф-ции, заданной дискретно.

Л инейная интерполяция: она состоит в том, что заданные точки соединяются прямолинейными отрезками и функция S(x) приближается к ломанной, с вершинами в данных точках. Для i-го интервала можно написать ур-е прямой, проходящей через точки и

Таким образом, при использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение аргумента х, а затем построить ур-е прямой по двум точкам, концами этого интервала, и найти значение y(x).

К вадратичная интерполяция: в качестве интерполяционной функции на отрезке принимается квадратный трехчлен. Ур-е кв. трехчлена при , которое содержит 3 неизв. коэффициента - . Для их определения необходимо 3 уравнения. Ими служат условия прохождения параболы через 3 точки - , которые можно записать в виде:

Решая эту систему лин. ур-й относительно , мы найдём коэффициенты квадратного трехчлена.

6. Многочлен Лагранжа

L_n(x)= , где p_ui(x)= ,i=0,1,…,n

Многочлен Ньютона

N(x_i+th)=y_i+t∆y_i+ ; i=0,1,…,n

7.Эмпирические формулы.

Пусть изучая неизвестную функцию. Зависимость y(x). Мы в расчете серии экспериментов получили таблицу значений.

X0	X1	X2	…	Xn
Y0	Y1	Y2	…	yn

Задача состоит в том, чтобы найти зависимость y=f(x), значение которого при x=x_i мало отличается от опытных данных y_i. Построенная т.о. ф-ла y=f(x) называется эмпирической. Задача на построение эмпирической формулы отличается от задач интерполирования тем, что график эмп. зависимости не проходит через узлы (x_i; y_i), что приводит к сглаживанию эмпирических данных, а интерполяционная формула повторила все ошибки эксперимента. Построение эмп ф-лы сост из 2-х этапов:

1. Подбор общего вида ф-лы

2. Опред наилучших значений содержащихся в ней параметров

Виды эмп ф-л:

1. Линейная зависимость y=ax+b (легко видеть после построения графика)

2. Степенная зависимость (м.б. сведена к линейной) U=lny 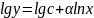Ù=lnα U=α Ù+β β=lgc

3. Показательная зав-ть также м.б. сведена к линейной.

4. Гиперболическая

Для определения параметров эмпир ф-лы, сущесв след метода:

1. Метод выбранных точек: пусть для с-мы определенных точек M_i(x_i;y_i) выбрана эмпир ф-ла y=f(x;a₁,a₂….a_n) На корд пл-ти XOY проводится плоская кривая Г опис точки M_i. На линии Г выбир с-мы из M точек с корд N_j , равноудаленных друг от друга. Параметры а₁…а_n м.б. найдены из с-мы ур-ний:

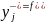
2. Метод средних. Если в эмпир т-ру подставить исход данные M_i(x_i;y_i) то левая и правая части будут не равны. Разности ε=f(x_i; a₁…a_n)-y_i называют упрощениями и предст собой расстоянию вертикали т. M_i от графика. Согласно методу средних за наилучшее положение Г приним то . для которых 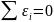. Для опред по методу ср постоянных a₁…a_m счит те, для которых сумма квадратов минимальна S(a₁…a_m)= ² Отсюда исп необход условие экстремума ФНП получаем: 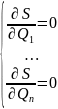Если сумма имеет единств решение то оно будет искомым.

Зам: метод наим квадр обл тем преимуществом. Что если сумма квадратов мала, то сами уклонения тоже малы.

Необходимое условие существования эмпир ф-мы: пусть например выберем вычислим y: ; ; ,=>

т.о. для существ степени завис необходимо чтобы среднему геом x_s значений x₁x_n соотв y_s знач y₁y_n, т.е. если x_i образует геом прогрессию, то значение y_i также должны образ геом прогрессию.