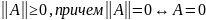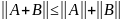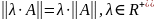Погрешность (задачи, метода, округлений). Абсолютная и относительная погрешность. Понятие устойчивости, корректности, сходимости.
При решении мат. задач почти неизбежно появление погрешностей 3 типов:
- погрешность задачи – связана с приближенным характером исходной содержательной модели, с невозможностью учесть все факторы в процессе изучение моделируемого явления. Для вычислителя погрешность задачи след. считать неустранимой или безусловной;
- погрешность метода – связана со способом решения поставленной математической задачи, и появляющаяся в результате подмены исходной математической модели другой. При создании численных методов закладывается возможность отслеживания и доведения их до сколь угодно малого уровня -> отношение погр. метода как к устранимой или условной;
- погр. округлений – обусловлена необходимостью выполнять арифметические операции над числами с усеченными до количества разрядов, зав. от применения вычислительной техники;
Эти погрешности в сумме дают полную погр. решения задачи.
Пусть А и а – два близких числа. Условимся считать А – точным, а – приближенным.
Величина
– абсолютная погрешность;
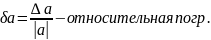Числа
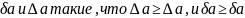называются оценками абсол. И относ.
погрешностей.
Устойчивость:
пусть по исходному значению величины
х находится значение величины у, если
исходная величина имеет абсол. порг.
,
то решении имеет погр.
.
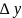Задача называется устойчивой по исходному
параметру х, если решение у непрерывно
от него зависит, т.е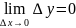
Корректность: задача называется поставленной корректно, если для любых значений исходных данных из некоторого класса её решение существует единственно и устойчиво по исходным данным.
Сходимость: означает близость получаемого численного решения задачи к истинному.
2. Решение линейных систем. Норма (матрицы, вектора) и понятие обусловленности. Прямые и итерационные методы решения.
Рассмотрим линейную алгебраическую систему, записанную в виде векторно-математ. уравнения
;
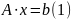А – невырожденная матрица (квадратная
матрица, определитель которой отличен
от нуля) nxn;
b
– ненулевой n-мерный
вектор
;
x
– n-мерный
вектор неизвестных
;
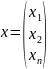Пусть
правая часть (1) получила приращение
,
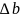т.е вместо истинного вектора b
воспользуемся
.
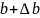Реакцией решения х на возмущение
правой части будет вектор поправок
,
т.е если х – решение (1), то
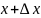– решение
.
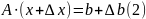Для того, чтобы сравнивать и оценивать
близость матриц (векторов), вводится
понятие нормы:
Норма
(матрицы, вектора) А
- действительное число
(норма А), удовлетворяющее условиям:
Длина вектора и есть норма, обратное не верно.
Норма
вектора –
выражение вида
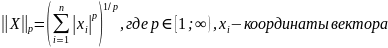
При
p=2:
При
p=1:
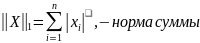
При
p=
:
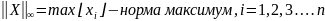
Обусловленность
- положительное число
(мера обусловленности) матрицы А.
Обозначают condA;
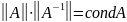
Методы решения систем линейных уравнений делятся на прямые и итерационные.
Прямые – используют конечные разности для вычисления неизвестных. Просты и наиболее универсальны.
Недостатки – требуют хранения в памяти ЭВМ сразу всей матрицы, не учитывают структуру матрицы, сильное накапливание погрешностей в процессе решения.
Итерационные – методы последовательных приближений, в которых необходимо задать начальное приближение и после этого с помощью некоторого алгоритма проводится один цикл вычислений – итерация.
Итерации проводятся для получения решений с треб. точностью.
«+» - не треб. хранения в памяти машины всей матрицы, погрешности не накапливаются.