
- •3) Основные законы электрических цепей
- •11)Индуктивная катушка в цепи синусоидального тока
- •2. Конденсатор
- •3. Катушка индуктивности
- •22) 2.1.2. Работа трансформатора под нагрузкой
- •23) Расчетное определение параметров схемы замещения трансформатора
- •36) Пуск и регулирование частоты вращения машин постоянного тока.
- •Структура оу
- •Вид обрабатываемого сигнала
22) 2.1.2. Работа трансформатора под нагрузкой
При подключении сопротивления нагрузки Zн к зажимам вторичной обмотки в ней появляется ток i2 и уравнения электрического состояния трансформатора можно записать в виде
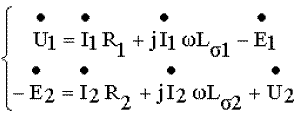
Эти уравнения, записанные в комплексной форме относительно эквивалентных синусоид, ничем не отличаются от соответствующих уравнений воздушного трансформатора. Анализируя работу трансформатора под нагрузкой, важно уяснить взаимосвязь тока в цепи нагрузки i2 с током, потребляемым трансформатором от сети, поскольку изменение мощности, отдаваемой трансформатором в нагрузку должно сопровождаться изменением мощности, потребляемой трансформатором от сети. Эта взаимосвязь устанавливается через уравнение магнитного состояния трансформатора.
При изучении воздушного трансформатора нами было установлено, что Ф=Ф1-Ф2, т.е. основной или рабочий поток трансформатора равен алгебраической сумме потоков взаимоиндукции первичной и вторичной обмоток Ф1и Ф2 или
![]() где λМ -
магнитная проводимость участка, по
которому замыкаются потоки взаимоиндукции.
(В соответствие с принципом Ленца
поток Ф1 направлен
встречно потоку Ф2.)Следовательно,
в режиме ХХ
где λМ -
магнитная проводимость участка, по
которому замыкаются потоки взаимоиндукции.
(В соответствие с принципом Ленца
поток Ф1 направлен
встречно потоку Ф2.)Следовательно,
в режиме ХХ ![]() ,а
под нагрузкой
,а
под нагрузкой ![]() Если
пренебречь напряжениями
1R1 и
Если
пренебречь напряжениями
1R1 и ![]() по
сравнению с ЭДС
по
сравнению с ЭДС ![]() ,
т.е. считать, что
,
т.е. считать, что ![]() ,
то поток в сердечнике будет однозначно
определяться приложенным напряжением,
как было показано выше. Следовательно,
поток в сердечнике при одинаковом
напряжении будет одинаковым как в режиме
ХХ, так и под нагрузкой, т.е.
,
то поток в сердечнике будет однозначно
определяться приложенным напряжением,
как было показано выше. Следовательно,
поток в сердечнике при одинаковом
напряжении будет одинаковым как в режиме
ХХ, так и под нагрузкой, т.е.
Фк=Ф или Фк= Ф1- Ф2. Физически взаимосвязь токов i1 и i2 объясняется следующим образом: в режиме ХХ ток холостого хода i1x создает поток в сердечнике Ф1x, обуславливающий ЭДС
![]() Ток i2,
протекающий через нагрузку, создает
поток Ф2,
стремящийся ослабить поток Ф.
Но уменьшение потока Ф приводит к
уменьшению ЭДС e1,
и, следовательно, к нарушению
равенства u1≈-e1.
Следовательно, ток i1начинает
возрастать и будет расти до тех пор,
пока поток не достигнет прежнего
значения Ф1x.
Из равенства Ф1x=
Ф1-
Ф2 или
Ток i2,
протекающий через нагрузку, создает
поток Ф2,
стремящийся ослабить поток Ф.
Но уменьшение потока Ф приводит к
уменьшению ЭДС e1,
и, следовательно, к нарушению
равенства u1≈-e1.
Следовательно, ток i1начинает
возрастать и будет расти до тех пор,
пока поток не достигнет прежнего
значения Ф1x.
Из равенства Ф1x=
Ф1-
Ф2 или ![]() 1x=
1-
2,
поскольку потоки синусоидальны, следует,
что
1x=
1-
2,
поскольку потоки синусоидальны, следует,
что
![]() 1x=
1-
2
Последнее
уравнение представляет собой закон
равновесия намагничивающих сил
трансформатора или уравнения магнитного
состояния трансформатора. Поскольку
1x=
1-
2
Последнее
уравнение представляет собой закон
равновесия намагничивающих сил
трансформатора или уравнения магнитного
состояния трансформатора. Поскольку ![]() ,
последнее уравнение можно записать в
виде
,
последнее уравнение можно записать в
виде
![]()
или
![]() ,
,
где ![]() -
приведенный ток вторичной обмотки.
-
приведенный ток вторичной обмотки.
Согласно последнему уравнению ток, потребляемый трансформатором от сети 1, имеет 2 составляющие: составляющая 1x создает рабочий поток в сердечнике и компенсирует потери в стали, составляющая 2′(нагрузочная составляющая) компенсирует размагничивающее действие на сердечник тока вторичной обмотки и обеспечивает поступление в трансформатор от сети мощности, отдаваемой в нагрузку.
Векторная диаграмма трансформатора, работающего на нагрузку, приведена на рис. 2.4.
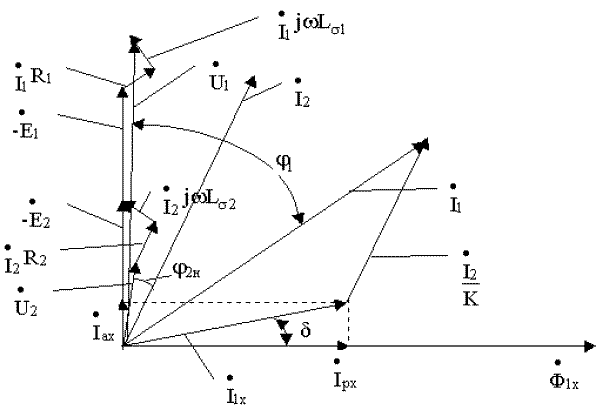 Рис.
2.4
Рис.
2.4
Порядок построения диаграммы:
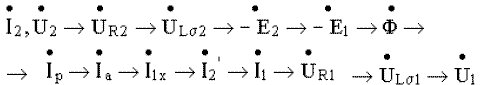
2.1.3. Схема замещения трансформатора В силу того, что уравнения электрического состояния трансформатора с ферромагнитным сердечником для эквивалентных синусоид аналогичны уравнениям воздушного трансформатора, то и схемы замещения этих трансформаторов во многом аналогичны. Особенность схемы замещения трансформатора с ферромагнитным сердечником состоит в наличии ветви с активной проводимостью g0, учитывающей потери в стали реального трансформатора (схема рис. 2.5).
Рис. 2.5
Участок схемы замещения между точками «а» и «б», аналогичный схеме замещения идеализированной катушки с ферромагнитным сердечником может быть заменен последовательной цепью из сопротивления R0 и XM (рис. 2.6) , называемой ветвью холостого хода. Через него проходит ток холостого хода 1x.
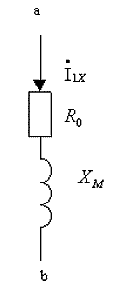 Рис.
2.6
Рис.
2.6
Параметры элементов схемы можно определить экспериментально на основании опытов холостого хода и короткого замыкания. Опыт ХХ проводиться для определения коэффициента трансформации К, потерь в стали и параметров ветви ХХ R0 и XM. Опыт ХХ проводится по схеме, приведенной на рис. 2.7 при номинальном напряжении на первичной обмотке U1=U1Н, установленном с помощью регулятора напряжения РН.
 Рис.
2.7
Рис.
2.7
При этом измеряется напряжение на вторичной обмотке U2x, ток первичной обмотки I1x и мощность (активная), потребляемая первичной цепью трансформатора P1x.
Как
уже ранее отмечалось, в режиме ХХ ![]() .
.
По данным опыта определяют
![]() -
коэффициент трансформации,
-
коэффициент трансформации,
![]() -
активное сопротивление ветви ХХ,
-
активное сопротивление ветви ХХ,
![]() -
фазовый сдвиг между напряжением и током
в режиме ХХ,
-
фазовый сдвиг между напряжением и током
в режиме ХХ,
![]() -угол
потерь,
-угол
потерь,
![]() -
полное сопротивление ветви ХХ,
-
полное сопротивление ветви ХХ,
![]() -
реактивное сопротивление ветви ХХ.
-
реактивное сопротивление ветви ХХ.
Опыт короткого замыкания проводиться для определения активных сопротивлений R1 и R2 и индуктивностей рассеяния Lσ1 и Lσ2 первичной и вторичной обмоток трансформатора. Опыт проводиться по схеме, приведенной на рис. 2-8 при закороченной вторичной обмотке.
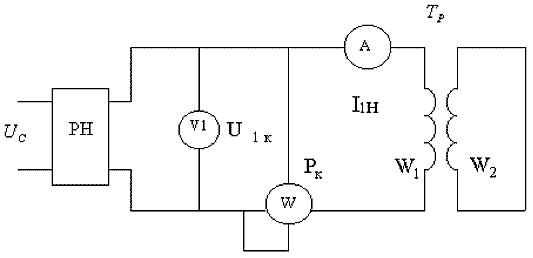 Рис.
2.8
Рис.
2.8
С помощью регулятора напряжения РН напряжение на первичной обмотке трансформатора постепенно увеличивается до значения U1K, при котором ток в первичной обмотке достигнет номинального тока I1Н. Это напряжение носит название напряжения короткого замыкания трансформатора. При этом измеряется мощность, потребляемая трансформатором P1K.
Обычно ![]() ,
поэтому поток в сердечнике, определяемый
напряжением мал. Следовательно, в режиме
КЗ можно пренебречь потерями в стали
трансформатора, исключить ветвь ХХ из
схемы замещения и представить эту схему
в виде рис. 2.9, где
,
поэтому поток в сердечнике, определяемый
напряжением мал. Следовательно, в режиме
КЗ можно пренебречь потерями в стали
трансформатора, исключить ветвь ХХ из
схемы замещения и представить эту схему
в виде рис. 2.9, где![]() .
.
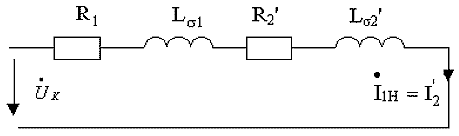 Рис.
2.9
Рис.
2.9
На основании данных измерений определяют
![]() -
процентное напряжение КЗ,
-
процентное напряжение КЗ,
![]() -
фазовый сдвиг между напряжением и током
в режиме КЗ,
-
фазовый сдвиг между напряжением и током
в режиме КЗ,
![]() -
активная составляющая напряжения КЗ
-
активная составляющая напряжения КЗ
![]() -
реактивная составляющая напряжения
КЗ.
-
реактивная составляющая напряжения
КЗ.
Поскольку поток в сердечнике трансформатора и потери в стали в режиме КЗ малы, считается, что вся мощность PK расходуется в меди первичной и вторичной обмоток. Тогда
![]()
и, следовательно,
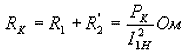 .
.
Так
как ![]() .
.
Полное сопротивление короткого замыкания

реактивное сопротивление КЗ
![]()
Поскольку 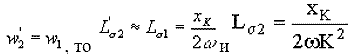 .
В паспорте или каталожных данных на
трансформатор часто указывается
величины Uк%, Uка%
и Uкр%
. Зная их, можно рассчитать
параметры RK и XK схемы
замещения следующим образом:
.
В паспорте или каталожных данных на
трансформатор часто указывается
величины Uк%, Uка%
и Uкр%
. Зная их, можно рассчитать
параметры RK и XK схемы
замещения следующим образом:
Т.к. ![]() ,
то
,
то ![]() .
.
Т.к. ![]() ,
то
,
то ![]()
