
- •1.Косий згин
- •2.Напруження при косому згині.
- •3.Силова площина.
- •4.Положення нейтральної лінії.
- •5.Переміщення при косому згині.
- •6.Умова міцності при косому згині.
- •7.Означення позацентрового розтягу.
- •8.Напруження при позацентровому розтязі.
- •9.Положення нейтральної лінії.
- •10.Ядро перерізу.
- •11.Умова міцності при позацентровому розтязі.
- •12.Означення та приклад.
- •13.Розрахунок на міцність згину з крученням.
- •14.Робота зовнішніх сил.Теорема Клапейрона.
- •15. Теорема Кастиліано
- •16 Теорема про взаємність робіт (Бетті).
- •17.Статично визначувані системи.Приклад.
- •18.Статично невизначувані системи.Приклад.
- •19.Ступінь математичної невизначуваності.
- •20.Інтеграл Мора.
- •21.Приклад застосування інтегралу Мора.
- •22.Спосіб Верещагіна.
- •23.Метод сил.Основні етапи розрахунку.
- •Основна система
- •Еквівалентна система
- •24.Канонічні рівняння методу сил.
- •25.Приклад застосування методу сил для 1 раз статично невизначуваної системи.
- •1. Стійка рівновага
- •2.Нестійка рівновага
- •3.Лінеаризовані рівняння рівноваги стиснутого стержня
- •5. Форми рівноваги
- •6.Формула Ейлера для визначення критичної сили стиснутого стрижня
- •8. Зведена довжина
- •9. Коефіцієнт зведення
- •10.Стійкість стержня за межею пропорційності.
- •11.Гнучкість стержня.
- •12.Класифікація стержнів за гнучкістю.
- •20.Послідовність проектного розрахунку стиснутих стержнів на стійкість
- •25.Вплив маси пружної системи на деформації і напруження при ударі
- •26.Міцність матеріалів при ударному навантаженні. Ударна в’язкість
- •37.Явище втоми та поняття витривалості матеріалу
- •38.Цикли напружень і їхні характеристики
- •39.Діаграма Веллера
- •40.Границя витривалості. Крива втоми
- •41Умовна межа витривалості
- •43 Коефіцієнт запасу втомної міцності
- •44 Діаграма Хея
- •45 Діаграма Гаффа-Поларда
20.Послідовність проектного розрахунку стиснутих стержнів на стійкість
задачу розв’язують методом послідовних наближень з перевіркою проміжних результатів за допомогою умови стійкості в такій послідовності:
- беруть довільне
значення коефіцієнта
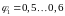 та обчислюють площу
та обчислюють площу
 перерізу стержня:
перерізу стержня:
|
|
відповідно до обчисленої площі визначають розміри перерізу або вибирають номер профілю із сортаменту;
визначають радіус інерції та гнучкість стержня, за якою з таблиць знаходять 1*;
порівнюють коефіцієнти 1 та 1* і, якщо розбіжність невелика, перевіряють умову стійкості (10.24); у разі істотної розбіжності значень 1 та 1* виконують друге наближення, для якого оптимальним значенням коефіцієнта зниження основного допустимого напруження 2 буде середньоарифметичне
|
|
Після цього повторюють всі зазначені дії.
Щоб отримати задовільний розв’язок, здебільшого треба виконати кілька наближень.
21.Основні типи динамічних задач
22.Урахування сил інерції при сталих прискореннях
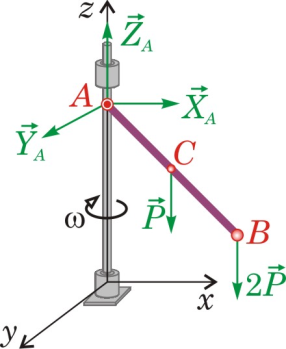 По принципу
Д’Аламбера
при
сталій кутовій швидкості всі точки
стержня мають лише нормальні прискорення,
які прямо пропорційні відстані точки
від осі обертання. Той
самий закон задовольняють і складові
сил інерції. Сила інерції точкової маси
В дорівнює добутку її маси на прискорення:
По принципу
Д’Аламбера
при
сталій кутовій швидкості всі точки
стержня мають лише нормальні прискорення,
які прямо пропорційні відстані точки
від осі обертання. Той
самий закон задовольняють і складові
сил інерції. Сила інерції точкової маси
В дорівнює добутку її маси на прискорення:
![]()
23.Ударні навантаження
Ударом називають навантаження, що передається тілу протягом малого проміжку часу і викликає в ньому значні прискорення, а отже і значні сили інерції. За характером прикладання сили до стержня розрізняють поздовжній, поперечний та крутний удари.
24.Динамічний коефіцієнт при ударі
дарне прикладення навантаження до пружної системи приводить до значного зростання напружень і переміщень у порівнянні із статичним прикладенням такого ж навантаження. Це збільшення оцінюється динамічним коефіцієнтом КД , що показує, у скільки разів напруги і переміщення при динамічному впливі навантаження будуть більше, ніж при статичному її прикладенні.
При згинальному ударі (рис.4.16)
σД = КД·σст; fД = КД·fст,
де σст і fст - напруга і прогин при статичному прикладенні сили Р;
σД і fД - ті ж величини при динамічному впливі сили Р.
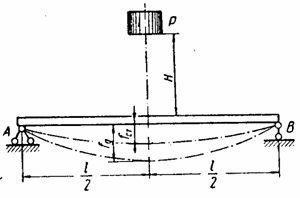
Наближена теорія удару виходить з того, що кінетична енергія падаючого вантажу цілком переходить у потенційну енергію деформації балки.
25.Вплив маси пружної системи на деформації і напруження при ударі
Якщо власна вага стержня Q і вага падаючого вантажу P (рис.12.1) – величини одного порядку, то інерцію маси стержня слід враховувати, оскільки це може суттєво вплинути на результати розрахунків. Якщо стержень безмасовий
|
(12.16) |
Якщо врахувати масу стержня, але привести її до місця удару, то
|
(12.17) |
де
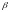 - коефіцієнт приведення розподіленої
маси стержня до точки удару.
- коефіцієнт приведення розподіленої
маси стержня до точки удару.
Розділивши (12.17)
на (12.16), отримаємо поправку
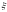 ,
яку треба внести до формули (12.6)
,
яку треба внести до формули (12.6)
|
(12.18) |
тоді формула динамічного коефіцієнта із врахуванням маси стержня набуде вигляду
|
(12.19) |

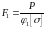 ;
; .
.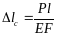 .
.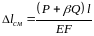 ,
,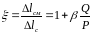 ,
,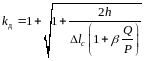 .
.