
- •1.Косий згин
- •2.Напруження при косому згині.
- •3.Силова площина.
- •4.Положення нейтральної лінії.
- •5.Переміщення при косому згині.
- •6.Умова міцності при косому згині.
- •7.Означення позацентрового розтягу.
- •8.Напруження при позацентровому розтязі.
- •9.Положення нейтральної лінії.
- •10.Ядро перерізу.
- •11.Умова міцності при позацентровому розтязі.
- •12.Означення та приклад.
- •13.Розрахунок на міцність згину з крученням.
- •14.Робота зовнішніх сил.Теорема Клапейрона.
- •15. Теорема Кастиліано
- •16 Теорема про взаємність робіт (Бетті).
- •17.Статично визначувані системи.Приклад.
- •18.Статично невизначувані системи.Приклад.
- •19.Ступінь математичної невизначуваності.
- •20.Інтеграл Мора.
- •21.Приклад застосування інтегралу Мора.
- •22.Спосіб Верещагіна.
- •23.Метод сил.Основні етапи розрахунку.
- •Основна система
- •Еквівалентна система
- •24.Канонічні рівняння методу сил.
- •25.Приклад застосування методу сил для 1 раз статично невизначуваної системи.
- •1. Стійка рівновага
- •2.Нестійка рівновага
- •3.Лінеаризовані рівняння рівноваги стиснутого стержня
- •5. Форми рівноваги
- •6.Формула Ейлера для визначення критичної сили стиснутого стрижня
- •8. Зведена довжина
- •9. Коефіцієнт зведення
- •10.Стійкість стержня за межею пропорційності.
- •11.Гнучкість стержня.
- •12.Класифікація стержнів за гнучкістю.
- •20.Послідовність проектного розрахунку стиснутих стержнів на стійкість
- •25.Вплив маси пружної системи на деформації і напруження при ударі
- •26.Міцність матеріалів при ударному навантаженні. Ударна в’язкість
- •37.Явище втоми та поняття витривалості матеріалу
- •38.Цикли напружень і їхні характеристики
- •39.Діаграма Веллера
- •40.Границя витривалості. Крива втоми
- •41Умовна межа витривалості
- •43 Коефіцієнт запасу втомної міцності
- •44 Діаграма Хея
- •45 Діаграма Гаффа-Поларда
17.Статично визначувані системи.Приклад.
Статично визначними називаються системи, для яких зовнішні реакції і всі внутрішні силові фактори можна визначити за допомогою рівнянь рівноваги і методу поперечних перерізів.
В таких системах в’язей є стільки скільки потрібно для рівноваги цієї системи.

18.Статично невизначувані системи.Приклад.
Статично невизначними називаються системи, для яких зовнішні реакції і всі внутрішні силові фактори не можна визначити за допомогою рівнянь рівноваги і методу поперечних перерізів.
В таких системах в’язів більше, ніж це необхідно для рівноваги. Ці в’язі є ніби зайвими, а зусилля в них називають зайвими невідомими.
За кількістю зайвих в’язів або зайвих невідомих зусиль встановлюють ступінь невизначеності системи S.
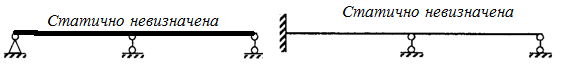
19.Ступінь математичної невизначуваності.
Ступінь статичної
невизначеності
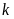 знаходять за формулою
знаходять за формулою
|
|
де
 - кількість реакцій у в’язах, що накладені
на балку;
- кількість реакцій у в’язах, що накладені
на балку;
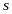 - кількість рівнянь рівноваги, що можна
скласти для даної балки. Наприклад, для
балки, що зображена на рис.1
- кількість рівнянь рівноваги, що можна
скласти для даної балки. Наприклад, для
балки, що зображена на рис.1
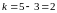 ,
тобто така балка двічі статично
невизначена.
,
тобто така балка двічі статично
невизначена.
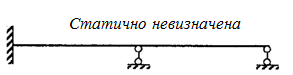
Рис.1
20.Інтеграл Мора.
Розглянемо прямий поперечний згин балки, що навантажена довільним зовнішнім навантаженням (рис. 1,а). Такий стан балки назвемо грузовим.
Знайдемо
прогин точки
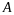 .
Для цього розвантажимо балку, а в напрямку
шуканого переміщення прикладемо
оди-ничну (безрозмірну) силу
.
Для цього розвантажимо балку, а в напрямку
шуканого переміщення прикладемо
оди-ничну (безрозмірну) силу
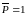 .
Такий стан балки назвемо одиничним.
.
Такий стан балки назвемо одиничним.
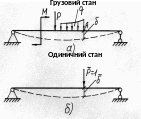
Визначимо віртуальну роботу зовнішніх і внутрішніх сил одиничного стану на переміщеннях, що викликані дією сил грузового стану.
Робота зовнішніх сил
|
Робота внутрішніх сил
|
тобто
|
- вираз згинного моменту в грузовому стані.
Якщо в
точці
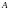 потрібно визначити кутове переміщення,
то при утворенні одиничного стану
замість одиничної сили
потрібно визначити кутове переміщення,
то при утворенні одиничного стану
замість одиничної сили
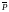 потрібно прикласти одиничний момент
потрібно прикласти одиничний момент
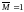 .
.
У випадку просторової задачі, наслідуючи формулу отримаємо
|
21.Приклад застосування інтегралу Мора.
22.Спосіб Верещагіна.
При визначенні переміщень дотримуються такої послідовності дій:
Будують епюри внутрішніх силових факторів від заданого навантаження (грузові епюри);
Відкинувши задане навантаження, в перерізі, де визначають переміщення, прикладають одиничну силу (або момент) у напрямку шуканого переміщення і будують епюри внутрішніх силових факторів (одиничні епюри);
„Перемножують” грузові епюри з одиничними за формулою.

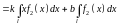
Добуток
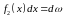 ,
а інтеграли
,
а інтеграли
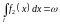 ;
;
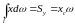 ,
де
,
де
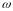 - площа, обмежена графіком функції
- площа, обмежена графіком функції
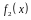 та віссю абсцис;
та віссю абсцис;
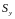 - статичний момент площі
- статичний момент площі
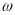 відносно осі y
.
відносно осі y
.
|
|
23.Метод сил.Основні етапи розрахунку.
Метод сил це найбільш загальний метод розкриття статичної невизначеності стержнів, балок та стержневих систем (рам, арок, ферм тощо).

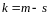 ,
,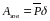 .
. ,
де
,
де
 ,
,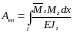 .
.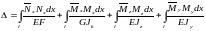 .
. ,
, ,
,