- •1.Косий згин
- •2.Напруження при косому згині.
- •3.Силова площина.
- •4.Положення нейтральної лінії.
- •5.Переміщення при косому згині.
- •6.Умова міцності при косому згині.
- •7.Означення позацентрового розтягу.
- •8.Напруження при позацентровому розтязі.
- •9.Положення нейтральної лінії.
- •10.Ядро перерізу.
- •11.Умова міцності при позацентровому розтязі.
- •12.Означення та приклад.
- •13.Розрахунок на міцність згину з крученням.
- •14.Робота зовнішніх сил.Теорема Клапейрона.
- •15. Теорема Кастиліано
- •16 Теорема про взаємність робіт (Бетті).
- •17.Статично визначувані системи.Приклад.
- •18.Статично невизначувані системи.Приклад.
- •19.Ступінь математичної невизначуваності.
- •20.Інтеграл Мора.
- •21.Приклад застосування інтегралу Мора.
- •22.Спосіб Верещагіна.
- •23.Метод сил.Основні етапи розрахунку.
- •Основна система
- •Еквівалентна система
- •24.Канонічні рівняння методу сил.
- •25.Приклад застосування методу сил для 1 раз статично невизначуваної системи.
- •1. Стійка рівновага
- •2.Нестійка рівновага
- •3.Лінеаризовані рівняння рівноваги стиснутого стержня
- •5. Форми рівноваги
- •6.Формула Ейлера для визначення критичної сили стиснутого стрижня
- •8. Зведена довжина
- •9. Коефіцієнт зведення
- •10.Стійкість стержня за межею пропорційності.
- •11.Гнучкість стержня.
- •12.Класифікація стержнів за гнучкістю.
- •20.Послідовність проектного розрахунку стиснутих стержнів на стійкість
- •25.Вплив маси пружної системи на деформації і напруження при ударі
- •26.Міцність матеріалів при ударному навантаженні. Ударна в’язкість
- •37.Явище втоми та поняття витривалості матеріалу
- •38.Цикли напружень і їхні характеристики
- •39.Діаграма Веллера
- •40.Границя витривалості. Крива втоми
- •41Умовна межа витривалості
- •43 Коефіцієнт запасу втомної міцності
- •44 Діаграма Хея
- •45 Діаграма Гаффа-Поларда
1.Косий згин
Косим називається такий вид згину, при якому площина дії згинного моменту в даному поперечному перерізі стержня не проходить через головну центральну вісь інерції цього перерізу.
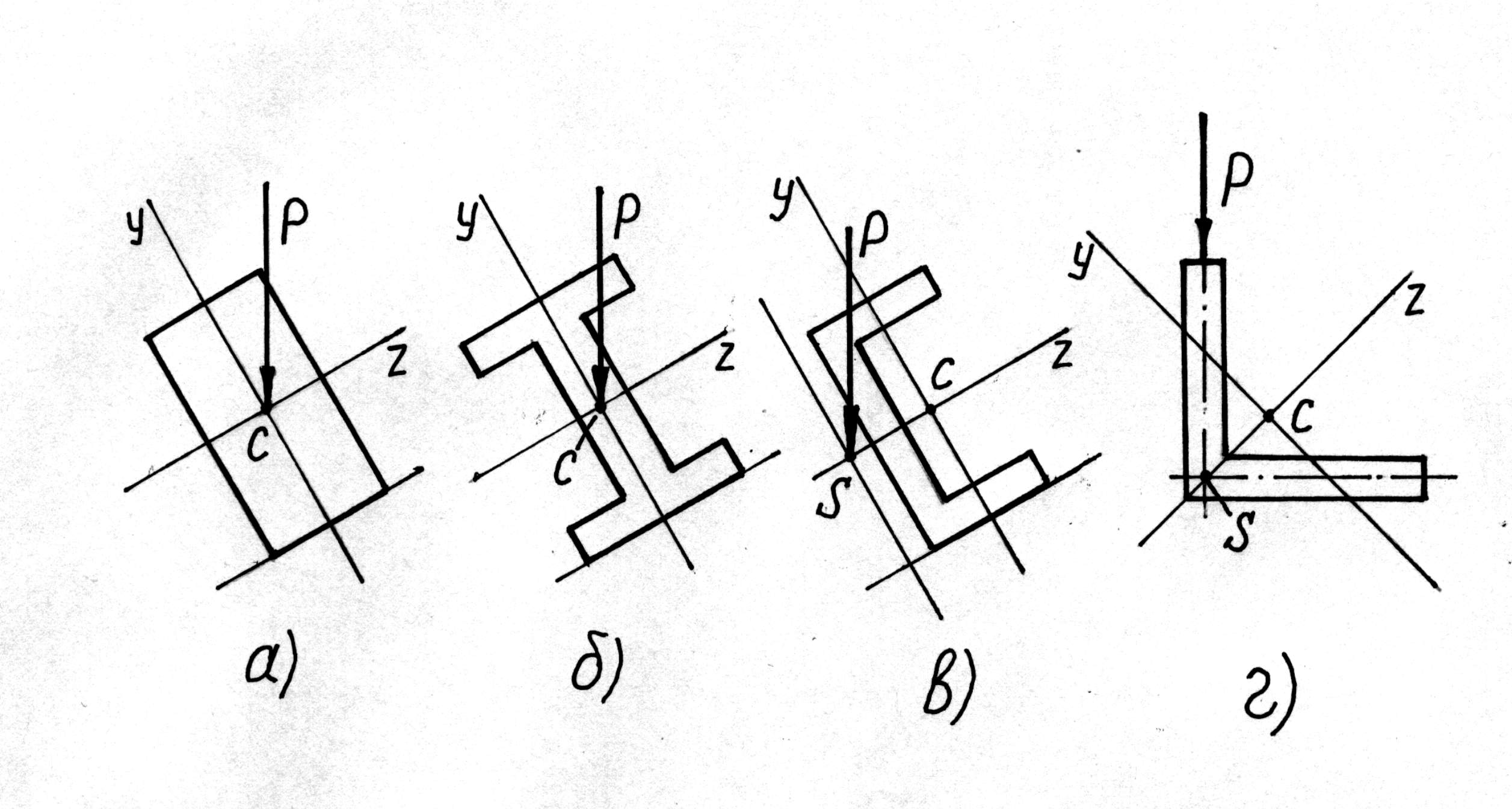
2.Напруження при косому згині.
Нормальні напруження в довільній точці поперечного перерізу балки при косому згині визначаємо за формулою
|
|
У формулу згинні
моменти
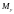 і
і
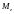 підставляють зі знаком плюс, якщо в
точках першої чверті їм відповідають
розтягуючі нормальні напруження, і зі
знаком мінус, якщо – стискаючі. Координати
точки
підставляють зі знаком плюс, якщо в
точках першої чверті їм відповідають
розтягуючі нормальні напруження, і зі
знаком мінус, якщо – стискаючі. Координати
точки
 і
і
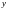 підставляють зі своїми знаками.
підставляють зі своїми знаками.
3.Силова площина.
Площина в якій діє навантаження називають силовою площиною.
4.Положення нейтральної лінії.
Рівняння нейтральної лінії отримаємо, розглядаючи її як геометричне місце точок перерізу, в яких нормальні напруження дорівнюють нулю
|
|
звідси
|
|
Це рівняння прямої з кутовим коефіцієнтом
|
|
Отже, щоб знайти
положення нейтральної осі потрібно
вісь
повернути на кут
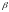 так, щоб вона проходила через центр ваги
перерізу і два квадранта, в яких моменти
і
викликають нормальні напруження різних
знаків (рис.
1)
так, щоб вона проходила через центр ваги
перерізу і два квадранта, в яких моменти
і
викликають нормальні напруження різних
знаків (рис.
1)
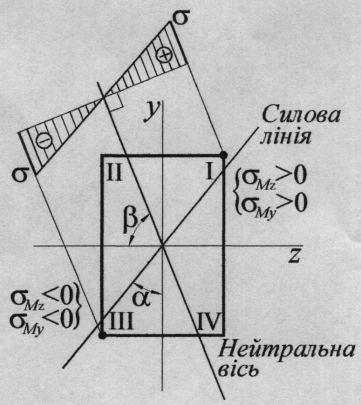
5.Переміщення при косому згині.
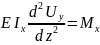 ,
,
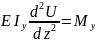 ,
,
де
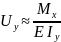 ; а
; а
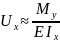 .
.
6.Умова міцності при косому згині.
Умова міцності для пластичного матеріалу має вигляд
|
(1) |
де
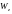 ,
,
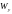 - моменти опору перерізу відносно осей
і
.
- моменти опору перерізу відносно осей
і
.
Для виконання проектного розрахунку рівняння (1) зручно представити у вигляді
|
(2) |
де
 - величина, якою попередньо задаються.
- величина, якою попередньо задаються.
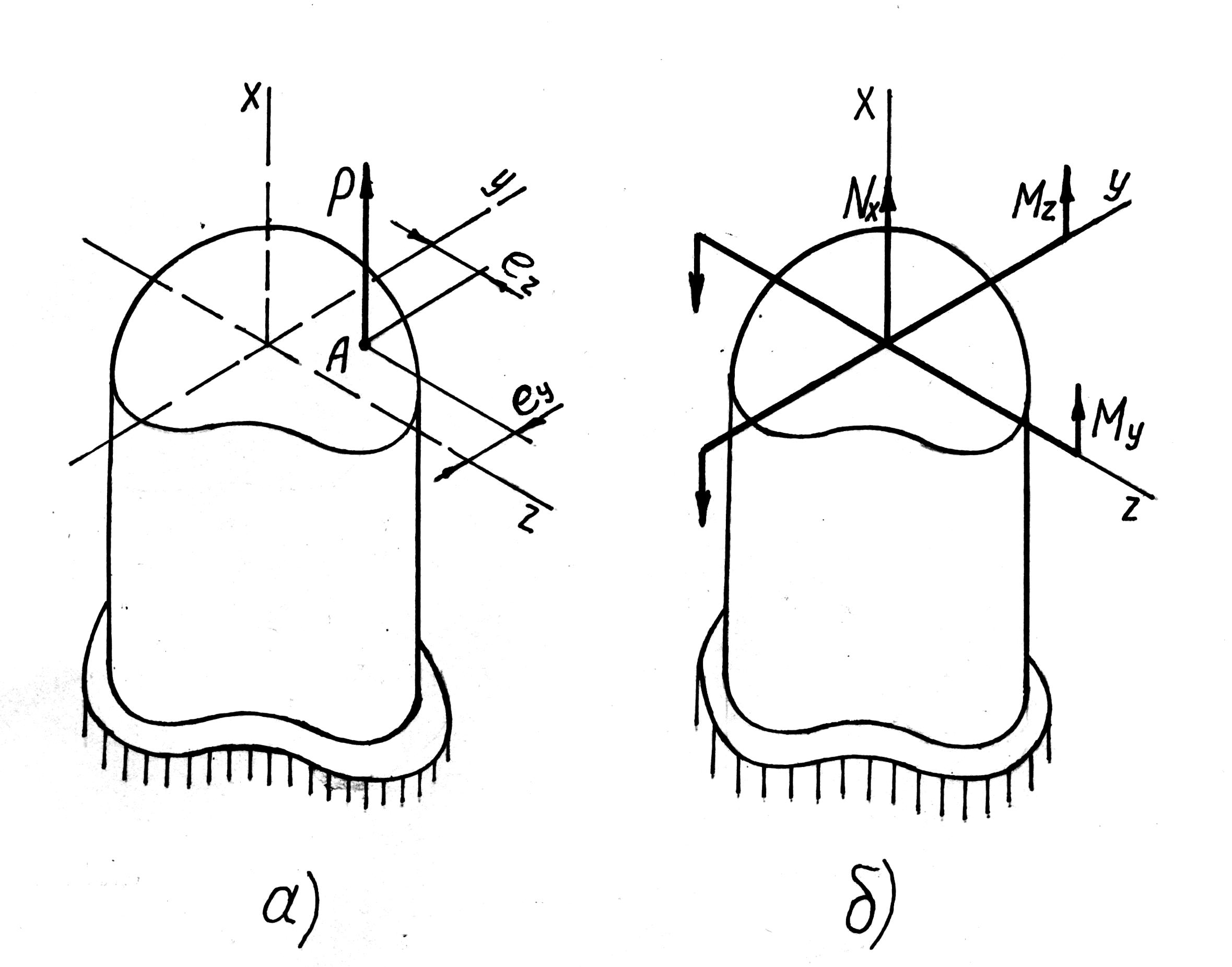
7.Означення позацентрового розтягу.
Позацентровим розтягом – стиском називають такий вид деформації, коли в поперечному перерізі стержня одночасно діють поздовжня сила і згинний момент.
|
Отже, ядром перерізу називається деяка зона навколо центра ваги поперечного перерізу, яка має таку властивість: якщо поздовжня сила прикладена в зоні ядра, то нормальні напруження в усіх точках поперечного перерізу матимуть однаковий знак.
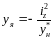 ;
;
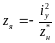 ,
,
8.Напруження при позацентровому розтязі.
Нормальне
напруження в довільній точці перерізу
з координатами
і
дорівнює сумі напружень від поздовжньої
сили
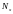 і згинних моментів
і
,
тобто
і згинних моментів
і
,
тобто
|
(1) |
Нехай точка, в якій шукаємо напруження, знаходиться в першій чверті перерізу.
|
(2) |
або
|
(3) |
де
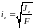 ,
,
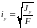 - радіуси інерції поперечного перерізу
стержня.
- радіуси інерції поперечного перерізу
стержня.
9.Положення нейтральної лінії.
Вираз (1) є рівнянням нейтральної осі:
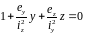 (1)
(1)
Його можна подати у вигляді рівняння прямої у відрізках
|
|
де
|
(2) |
відрізки, що відтинає нульова лінія на осях координат (рис. 1).
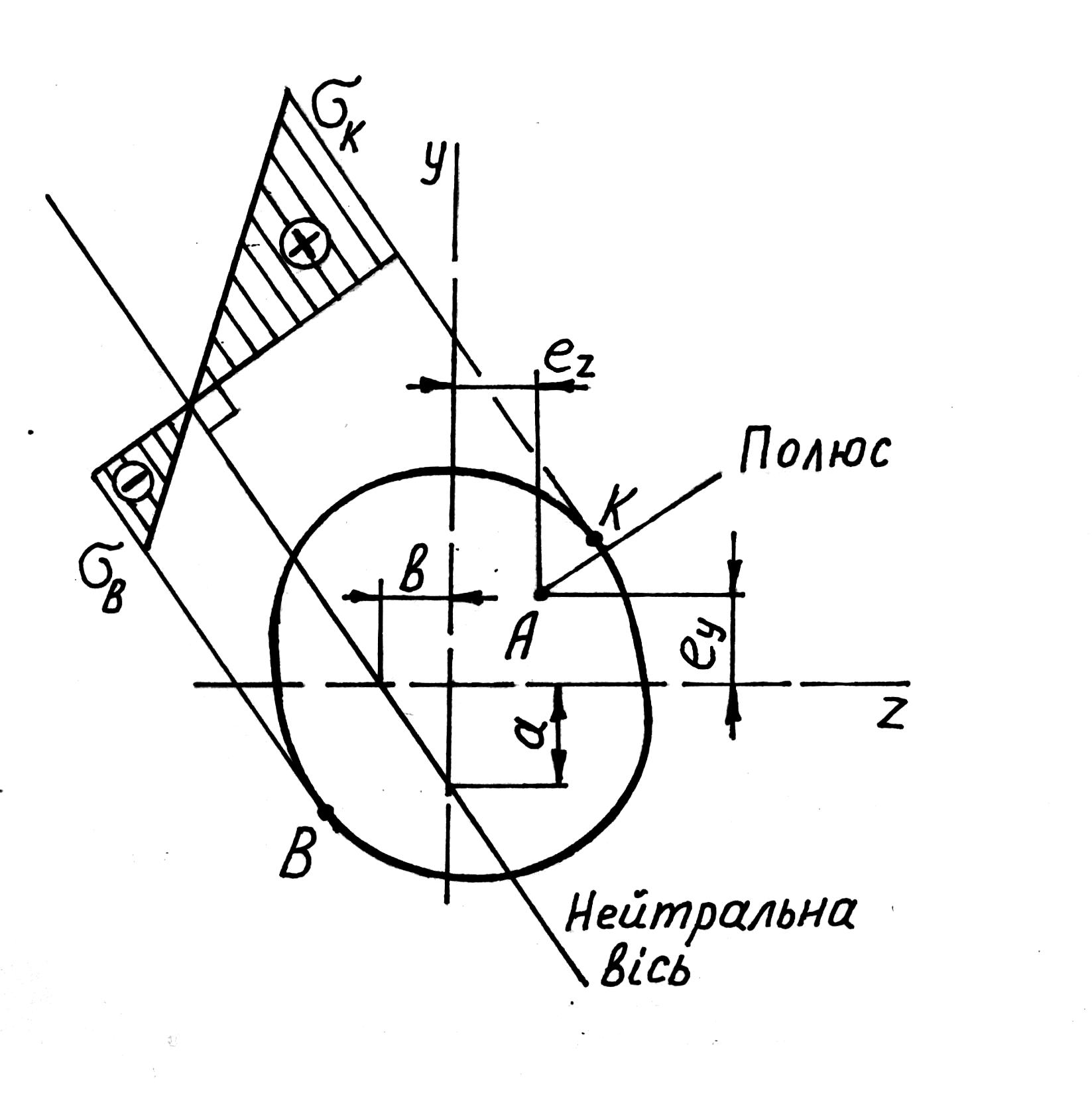
положення нейтральної осі не залежить від величини і знаку сили
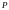 ;
;нейтральна вісь і полюс лежать з різних боків від початку координат;
чим далі від початку координат розміщено полюс, тим ближче до центру ваги перерізу проходить нейтральна вісь;
якщо полюс розміщено на головній центральній осі, то нульова лінія перпендикулярна до цієї осі;
якщо полюс рухається вздовж деякої прямої, то нейтральна вісь обертається навколо деякої точки.

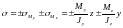 .
(1)
.
(1)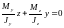 ,
,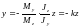 .
.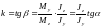 .
.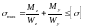 ,
,
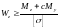 ,
,
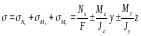 .
.
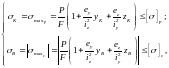
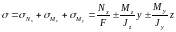 .
.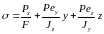 ,
, ,
, ,
,