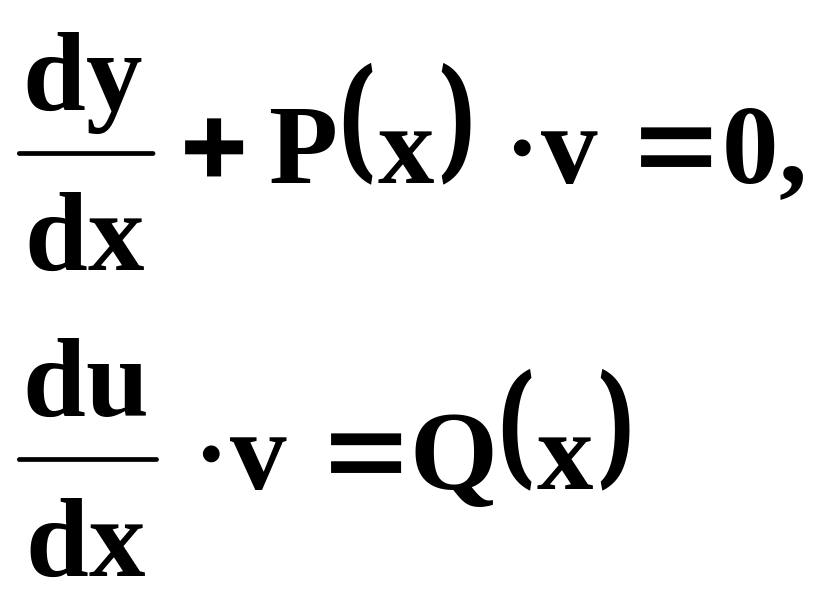- •Министерство образования и науки российской федерации
- •Кемерово 2012
- •Выбор номеров задач контрольной работы
- •Методические указания к контрольной работе
- •3. Теория функций комплексного переменного
- •3.1. Комплексные числа и действия над ними.
- •3.2. Алгебраические действия над комплексными числами.
- •4. Обыкновенные дифференциальные уравнения
- •Дифференциальные уравнения первого порядка
- •Общее решение однородного уравнения
- •Частное решение неоднородного уравнения
- •Обыкновенные дифференциальные уравнения
- •Список рекомендуемой литературы
Дифференциальные уравнения первого порядка
Тип дифферен-циального уравнения пер-вого порядка |
Вид уравнения |
Метод решения |
1. С разделяю-щимися пере-менными |
|
|
2. Однородное |
|
Подстановка
|
3. Линейное |
|
Подстановка
приводит
к уравнениям первого типа
|
произвольную постоянную для полагаем равной нулю. Получаем уравнение для нахождения функции
![]()
![]() .
.
Решение исходного уравнения имеет вид
![]() .
.
При решении задач № 121-150 используются приёмы решения дифференциальных уравнений второго порядка с постоянными коэффициентами, изложенные в литературе [2, т. 2, гл. VI, § 8, 9, с. 186 - 197; 4, п. 12.11-12.13, с. 279-286].]..
Для нахождения общего решения однородного дифференциального уравнения используется табл. 3, а для нахождения частного решения неоднородного дифференциального уравнения используется табл. 4.
Пример. Найти частное решение дифференциального уравнения
![]() ,
,
удовлетворяющее
начальным условиям
![]() .
.
Таблица 3
Общее решение однородного уравнения
Вид общего решения однородного уравнения |
Корни характеристического уравнения |
1.
|
|
2.
|
– вещественные,
|
3.
|
– комплексные,
|
Решение.
Общее решение неоднородного уравнения
можно записать в виде
![]() ,
где
,
где
![]() – общее решение однородного уравнения
– общее решение однородного уравнения
![]() ,
,
которое
определяется по табл. 3, а
![]() – частное решение неоднородного
уравнения, которое определяется по
табл. 4.
– частное решение неоднородного
уравнения, которое определяется по
табл. 4.
Для определения составим характеристическое уравнение
![]() .
.
Его
корни
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Так
как правая часть уравнения
![]() ,
то
,
то
![]() .
.
Здесь
![]() .
.
![]() .
.
![]()
![]() Подставив
эти значения в наше уравнение, получим
Подставив
эти значения в наше уравнение, получим
![]()
Таблица 4
Частное решение неоднородного уравнения
Вид правой части неод-нородного дифференци-ального уравнения |
Вид частного решения |
|
|
|
|
Сократим
на
![]() и сгруппируем члены с
и сгруппируем члены с
![]()
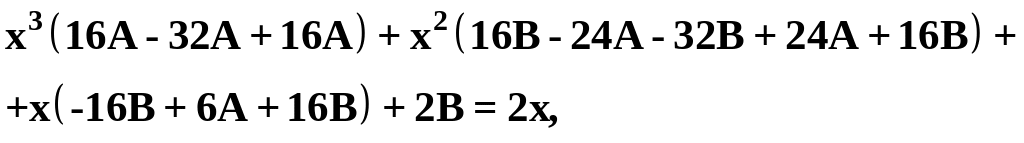
или
![]() .
.
Приравниваем
коэффициенты многочленов, стоящих в
левой и правой части равенства, при
одинаковых степенях
![]() .
Получаем систему уравнений для определения
.
Получаем систему уравнений для определения
![]() .
.
![]()
Итак,
![]() .
.
Общее решение неоднородного уравнения имеет вид
![]() ,
отсюда
,
отсюда
![]() .
.
Подставляя
в эти выражения начальные условия
![]() ,
найдём
,
найдём
![]() .
.
![]()
Итак, искомое решение имеет вид
![]() .
.
Пример. Найти частное решение дифференциального уравнения
![]() ,
,
удовлетворяющее
начальным условиям
![]() .
.
Решение. Общее решение неоднородного уравнения можно записать в виде , где – общее решение однородного уравнения
![]() ,
,
которое определяется по табл. 3, а – частное решение неоднородного уравнения, которое определяется по табл. 4.
Для определения составим характеристическое уравнение
![]() .
.
Его
корни
![]() .
.
Согласно
таблице 3
![]() ,
то есть
,
то есть
![]() .
.
Для
определения
используем табл. 4. Так как
![]() ,
то
,
то
![]() .
Следовательно,
.
Следовательно,
![]() .
.
Для определения подставим в первоначальное уравнение
![]() ,
,
![]() .
.
Тогда уравнение примет вид
![]()
Приравнивая
коэффициенты при
![]() и
и
![]() в левой и правой части этого уравнения,
получим систему
в левой и правой части этого уравнения,
получим систему
![]()
![]()
![]() .
.
Общее решение нашего уравнения имеет вид
![]() .
.
Отсюда
![]()
Найдём из начальных условий постоянные .
![]()
Итак, искомое решение имеет вид
![]() .
.
Контрольная работа №2
Интегралы.
1-30. Вычислить неопределённые интегралы.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
31-60. Задачи на геометрические приложения определённого интеграла
Найти площади частей, на которые круг
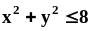 делится параболой
делится параболой
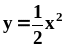 .
.Найти площадь фигуры, ограниченной линией
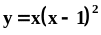 и осью абсцисс
и осью абсцисс
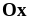 .
.Найти длину дуги параболы от точки
 до точки
до точки
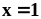 .
.Найти объём тела, образованного вращением вокруг оси фигуры, ограниченной линиями и
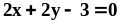 .
.Найти объём тела, образованного вращением вокруг оси фигуры, ограниченной линиями
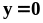 и
и
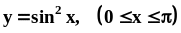 .
.Найти площадь фигуры, ограниченной параболами
 и
и
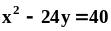 .
.Найти площадь фигуры, ограниченной линией
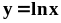 и прямыми
и прямыми
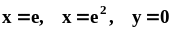 .
.Найти длину дуги кривой
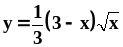 между точками её пересечения с осью
между точками её пересечения с осью
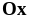 .
.
Вычислить объём тела, образованного вращением вокруг оси фигуры, ограниченной линиями
 .
.
Найти длину дуги кривой от точки
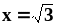 до точки
до точки
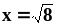 .
.
Вычислить площадь криволинейной трапеции, ограниченной линией
 и осью абсцисс
.
и осью абсцисс
.Найти объём тела, образованного вращением вокруг оси фигуры, ограниченной линиями
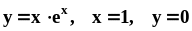 .
.Найти площади фигур, на которые парабола
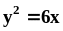 делит круг
делит круг
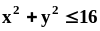 .
.Вычислить площадь фигуры, заключённой между линией
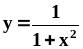 и параболой
и параболой
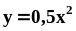 .
.Найти объём тела, образованного вращением вокруг оси
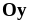 фигуры, ограниченной линиями
фигуры, ограниченной линиями
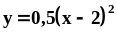 и
и
 .
.Найти длину дуги кривой
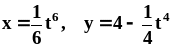 между точками её пересечения с осями
координат.
между точками её пересечения с осями
координат.Найти объём тела, образованного вращением вокруг оси фигуры, ограниченной линиями
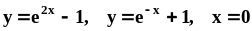 .
.Найти длину дуги кривой
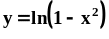 от точки
до точки
от точки
до точки
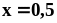 .
.Вычислить площадь фигуры, ограниченной линиями и
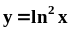 .
.Найти площадь фигуры, ограниченной линией
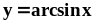 и прямыми
и прямыми
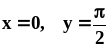 .
.Найти длину дуги кривой
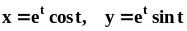 от
от
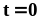 до точки
до точки
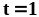 .
.Найти объём тела, образованного вращением параболического сегмента с основанием
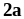 и высотой
и высотой
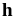 вокруг высоты.
вокруг высоты.Вычислить площадь фигуры, ограниченной линиями
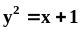 и
и
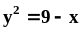 .
.Вычислить площадь фигуры, ограниченной линиями
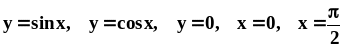 .
.Найти длину дуги астроиды
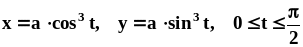 .
.Найти длину дуги полукубической параболы
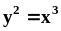 от начала координат до точки
от начала координат до точки
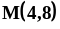 .
.Фигура ограничена кривой
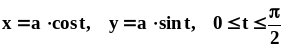 и осями координат
и осями координат
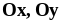 Найти объём тела вращения.
Найти объём тела вращения.Вычислить площадь фигуры, ограниченной линиями
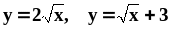 и осью
.
и осью
.Вычислить площадь фигуры, ограниченной кривыми
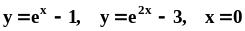 .
.найти площадь фигуры, ограниченной кривыми
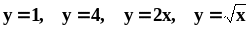 .
.
Задачи № 61-90. Задания: а) представить комплексное число в тригонометрической форме, б) представить комплексное число в показательной форме; в) выполнить указанные действия над комплексными числами, г) вычислить корень или решить уравнение.
61.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
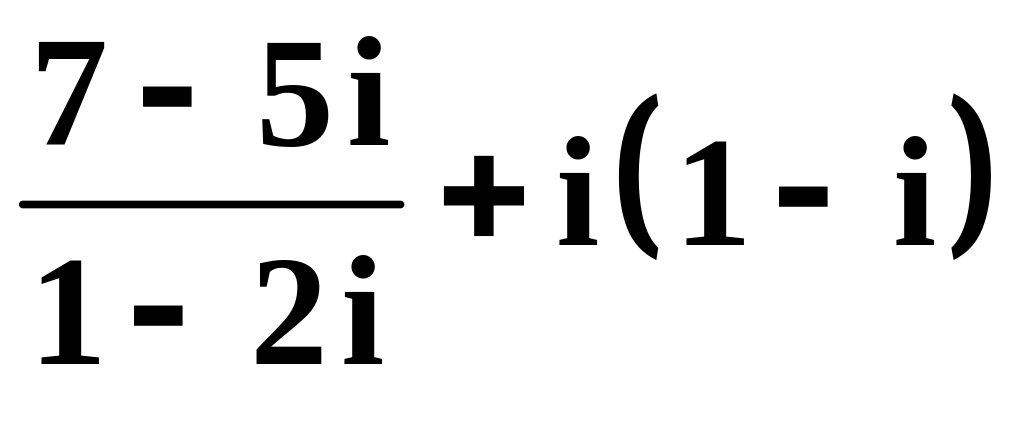 ,
г)
,
г)
![]() ;
;
62.
а)
![]() б)
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ;
;
63.
а)
![]() б)
б)
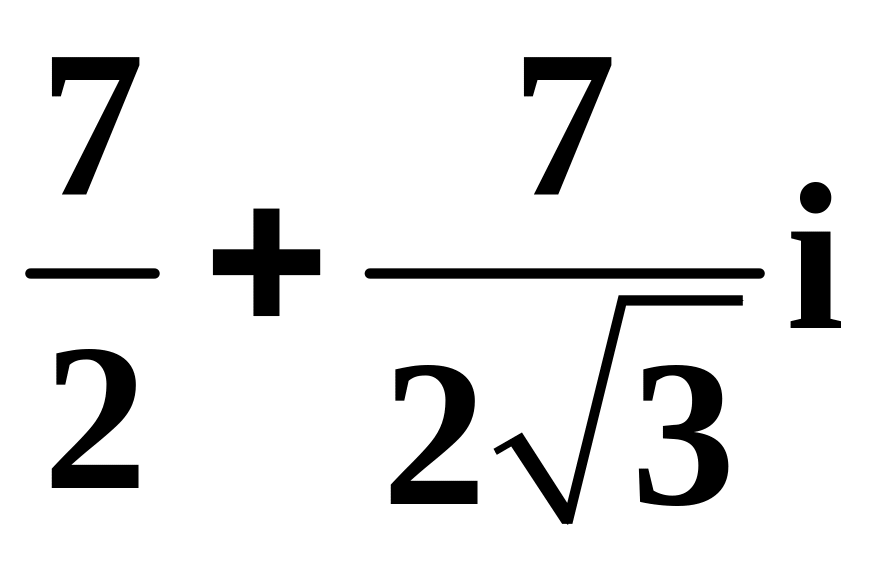 ,
в)
,
в)
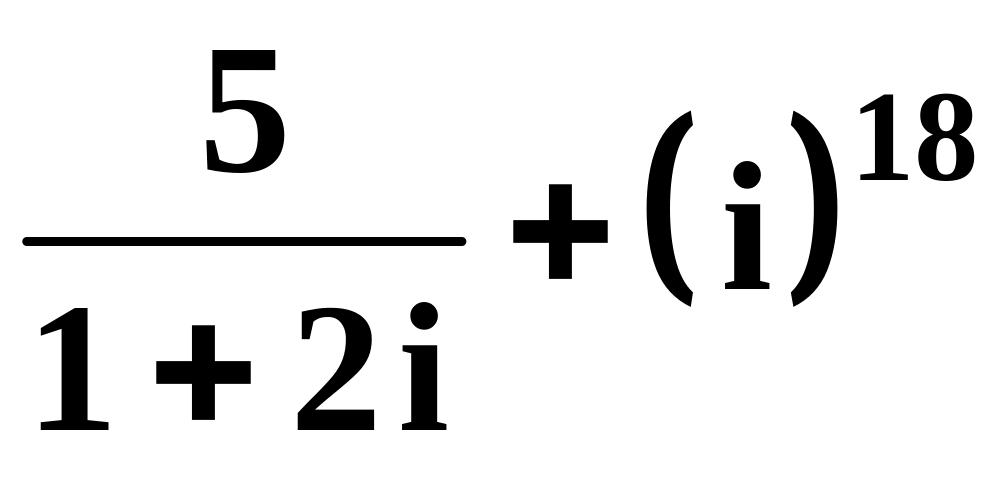 ,
г)
,
г)
![]() ;
;
64.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ;
;
65.
а)
![]() ,
б)
,
б)
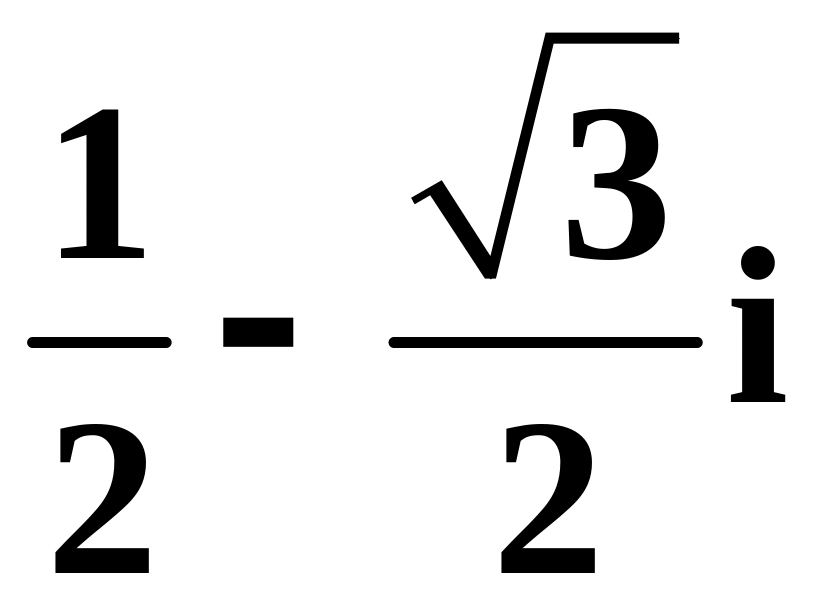 ,
в)
,
в)
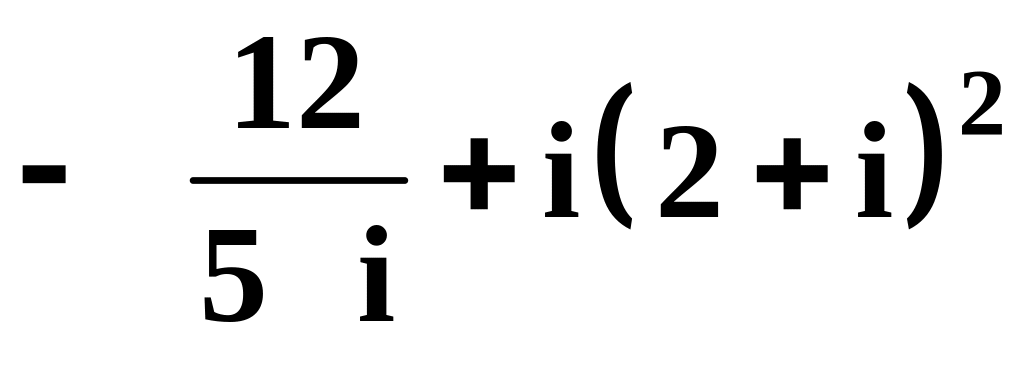 ,
г)
,
г)
 ;
;
66.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
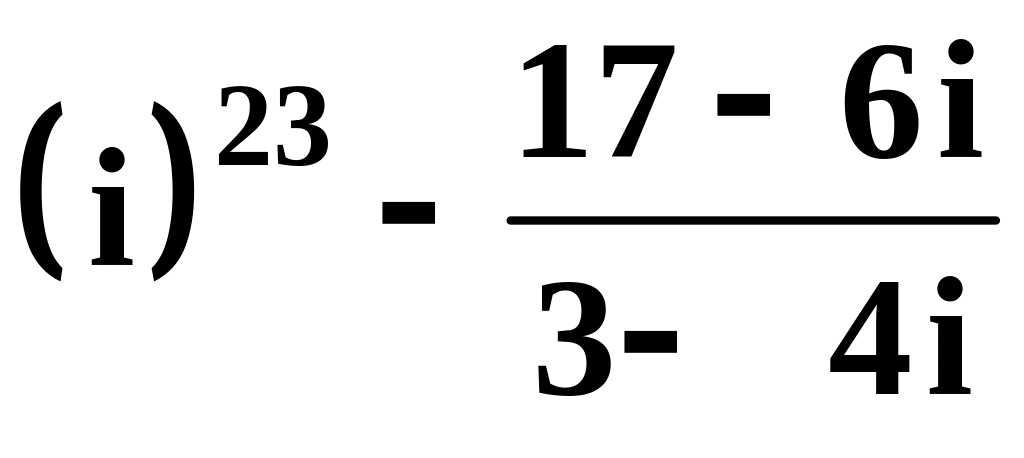 ,
г)
,
г)
![]() ;
;
67.
а)
![]() ,
б)
,
б)
![]() в)
в)
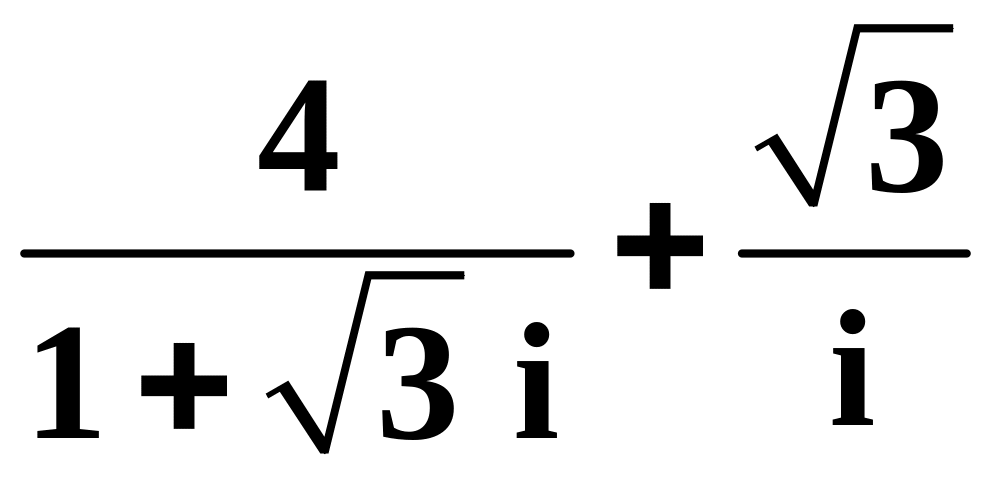 ,
г)
,
г)
![]() ;
;
68.
а)
![]() ,
б)
,
б)
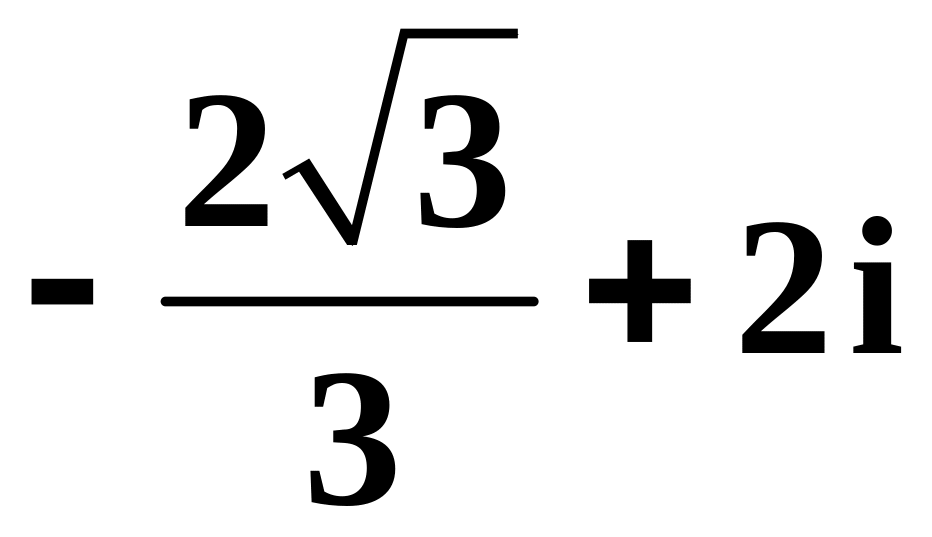 в)
в)
![]() ,
г)
,
г)
![]() ;
;
69.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ;
;
70.а)
![]() ,
б)
,
в)
,
б)
,
в)
![]() ,
г)
,
г)
![]() ;
;
71.
а)
![]() б)
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ;
;
72.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
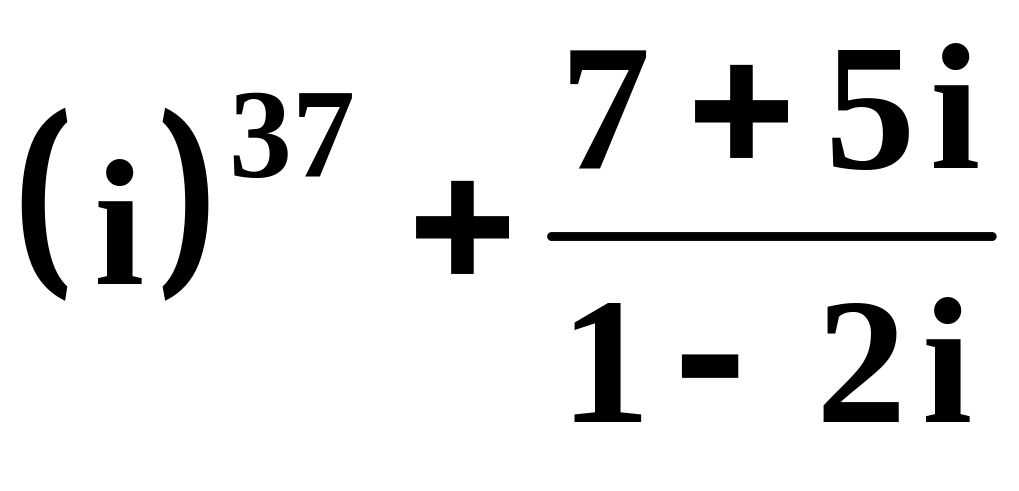 ,
г)
,
г)
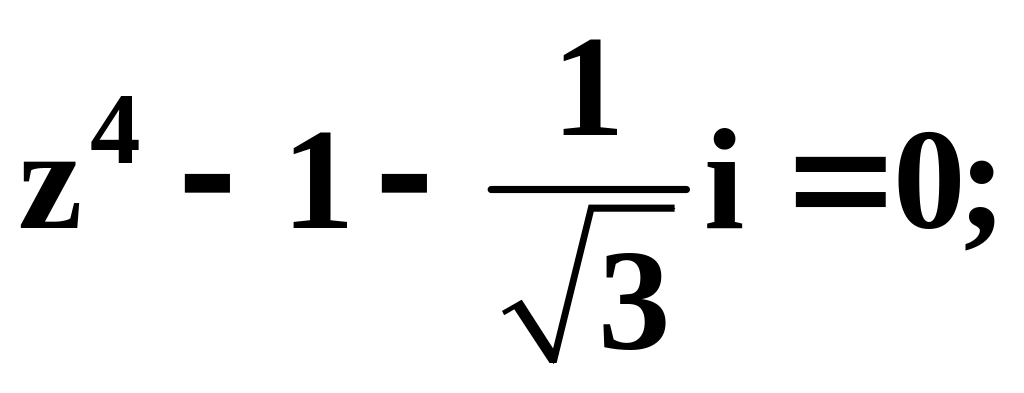
73.а)
![]() ,
б)
,
б)
![]() в)
в)
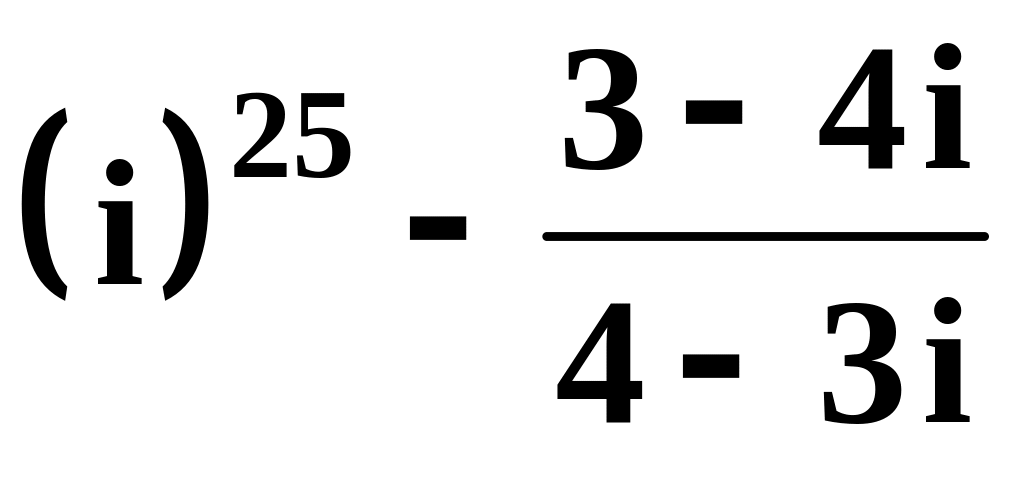 ,
г)
,
г)
![]() ;
;
74.
а)
,
б)
,
в)
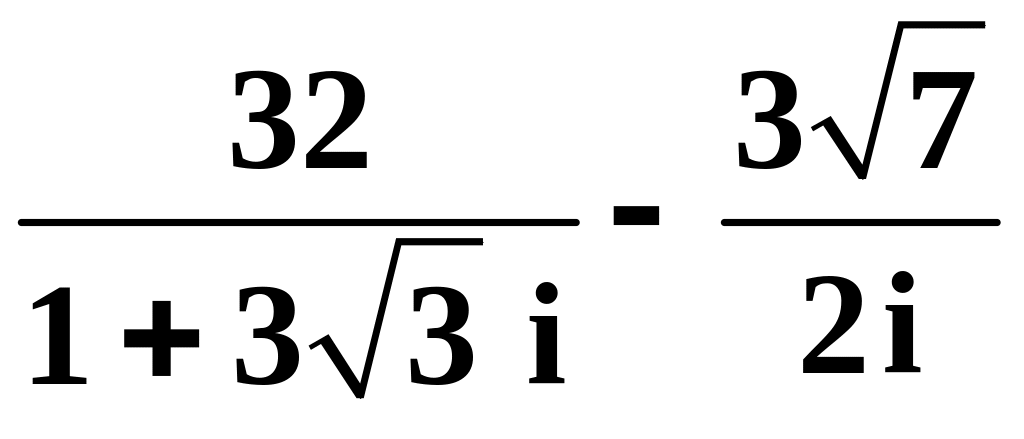 ,
г)
,
г)
![]() ;
;
75.
а)
![]() ,
б)
в)
,
б)
в)
 ,
г)
,
г)
![]() ;
;
76.
а)
![]() ,
б)
,
в)
,
б)
,
в)
![]() ,
г)
,
г)
![]() ;
;
77.
а)
![]() ,
б)
,
в)
,
б)
,
в)
![]() ,
г)
,
г)
![]() ;
;
78.
а)
![]() ,
б)
в)
,
б)
в)
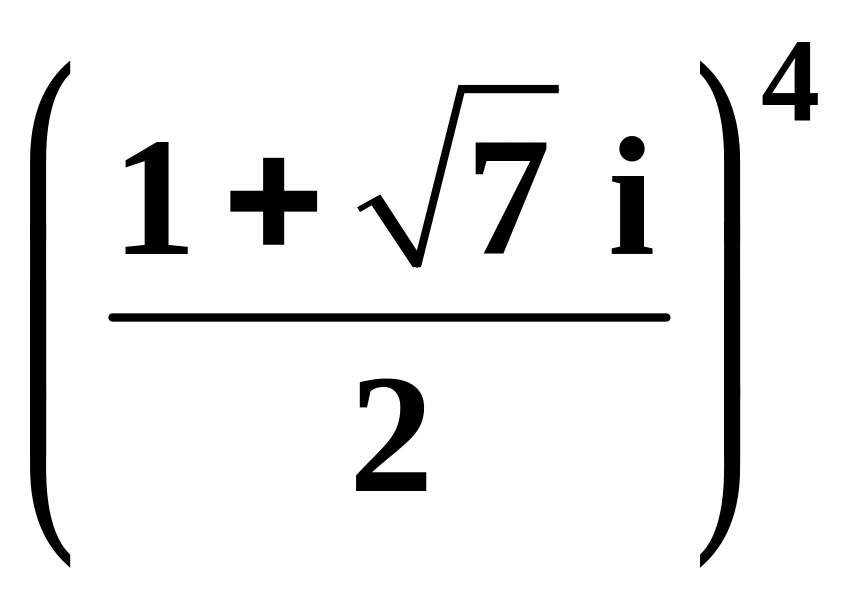 ,
г)
,
г)
![]() ;
;
79.
а)
![]() ,
б)
,
в)
,
б)
,
в)
![]() ,
г)
,
г)
![]() ;
;
80.
а)
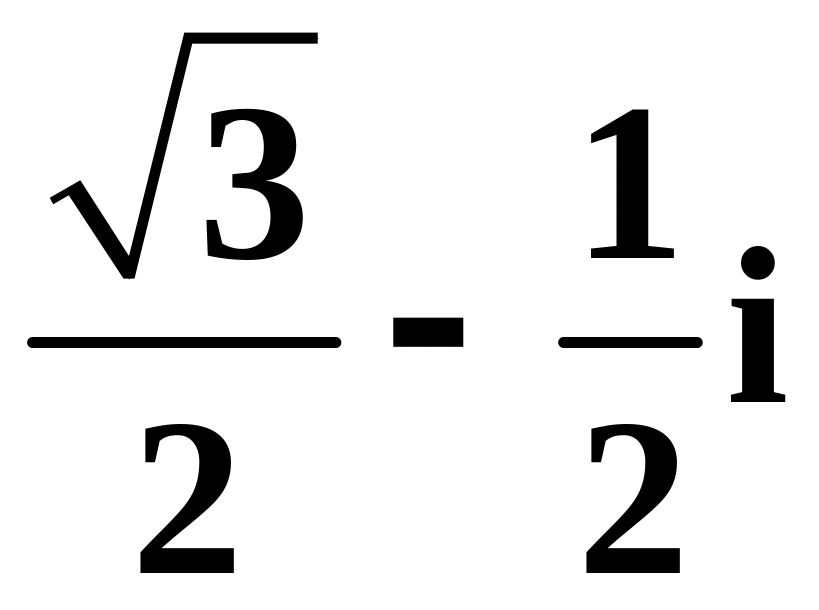 ,
б)
,
б)
![]() ,
в)
,
в)
 ,
г)
,
г)
![]() ;
;
81.
а)
,
б)
![]() ,
в)
,
в)
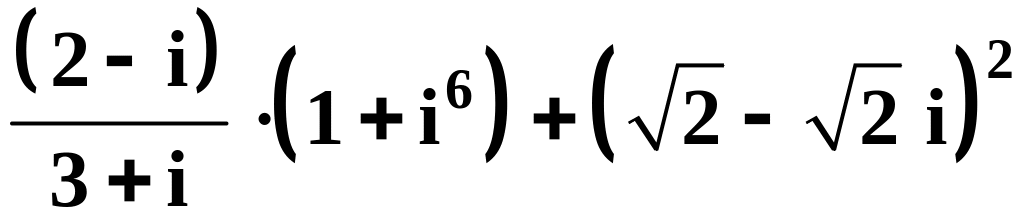 ,
г)
,
г)
![]() ;
;
82.
а)
![]() ,
б)
,
б)
![]() ,
в)
,
в)
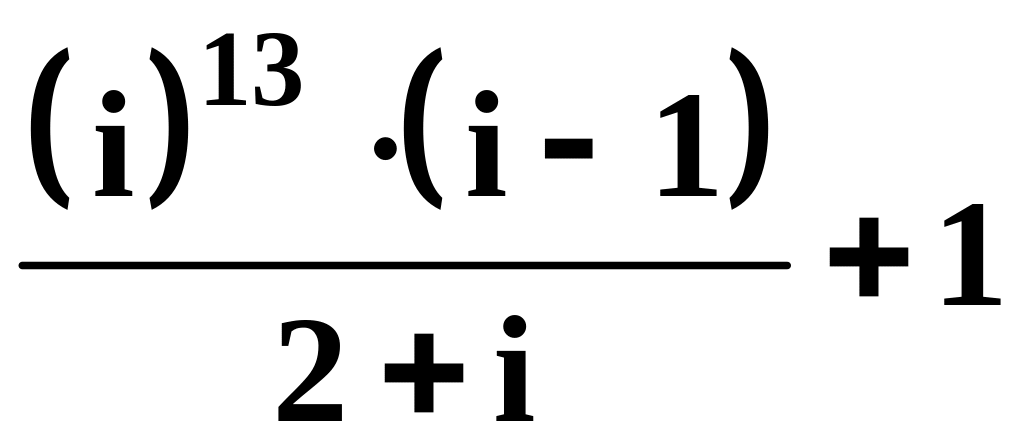 ,
г)
,
г)
![]() ;
;
83.а)
 ,
б)
,
б)
![]() ,
в)
,
в)
![]() ,
г)
,
г)
![]() ;
;
84.
а)
![]() ,
б)
,
в)
,
г)
,
б)
,
в)
,
г)
![]() ;
;
85.
а)
,
б)
,
в)
,
г)
![]() ;
;
86.
а)
,
б)
,
в)
,
г)
![]() ;
;
87.
а)
![]() ,
б)
,
в)
,
г)
,
б)
,
в)
,
г)
![]() ;
;
88.
а)
![]() ,
б)
,
в)
,
г)
,
б)
,
в)
,
г)
![]() ;
;
89.
а)
![]() ,
б)
,
в)
,
г)
,
б)
,
в)
,
г)
![]() ;
;
90.
а)
![]() ,
б)
,
в)
,
б)
,
в)
 ,
г)
,
г)
![]() .
.