
- •1. Последовательности. Определение,
- •2.Предел последовательности. Сходимость.
- •3.Свойства сходящихся последовательностей.
- •4. Признаки сходимости последовательностей.
- •5.Определение функции. Способы задания функции.
- •6.Классификация основных элементарных функций.
- •7. Предел функции. Теоремы о пределах.
- •8. Односторонние пределы. Несобственные пределы.
- •9. Непрерывность функции в точке.
- •10. Непрерывность функции в интервале. Действия с непрерывными функциями.
- •11.Разрывы функций. Классификация разрывов.
- •12.Производная функции. Геометрическийс мысл производной.
- •13.Теоремы о производной суммы, произведения и частного.
- •14. Производная сложной и обратной функции.
- •15. Дифференциал, связь дифференциала и приращения функции.
- •16.Производные и дифференциалы высших порядков.
- •17.Производные основных элементарных функций.
- •18. Теорема Роля. Теорема Лагранжа.
- •19. Теорема Коши. Формула Тейлора и Маклорена.
- •20. Раскрытие неопределенности по правилу Лопиталя.
- •21.Экстремум функции, точки перегиба, асимптоты.
- •22. Правила исследования функций.
- •23. Определение функции нескольких переменных. Линии уровня.
- •24. Предел функции нескольких переменных.
- •25. Непрерывность функции нескольких переменных в точке и в области.
- •26. Дифференцирование функций нескольких переменных.
- •27. Частные производные высших порядков. Теорема об изменении порядка дифференцирования.
- •28.Сложная функция двух переменных ее производная.
- •29. Дифференциал функции двух переменных первого и высших порядков.
7. Предел функции. Теоремы о пределах.
Определение.
Число
называется
пределом функции
при
,
стремящемся к бесконечности, если для
любого, даже сколь угодно малого
положительного числа
,
найдется такое положительное число
![]() (зависящее от
;
(зависящее от
;
![]() ),
что для всех
таких, что
),
что для всех
таких, что
![]() ,
верно неравенство:
,
верно неравенство:
![]() .
.
Определение.
Число
называется
пределом функции
при
,
стремящемся к
![]() (или в точке
),
если для любого, даже сколь угодно малого
положительного числа
,
найдется такое положительное число
(или в точке
),
если для любого, даже сколь угодно малого
положительного числа
,
найдется такое положительное число
![]() (зависящее от
;
(зависящее от
;
![]() ),
что для всех
,
не равных
и удовлетворяющих условию
),
что для всех
,
не равных
и удовлетворяющих условию
![]() ,
выполняется неравенство:
.
,
выполняется неравенство:
.
Теоремы о пределах:
Функция не может иметь более одного предела.
Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
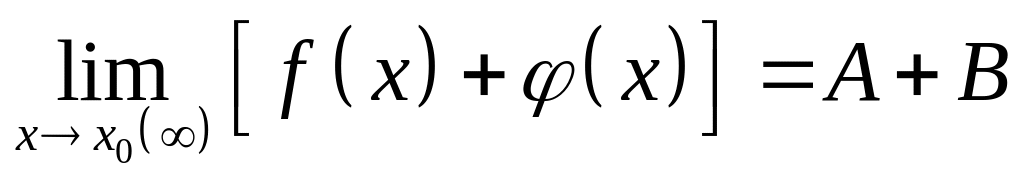 .
.Предел произведений конечного числа функций равен произведению пределов этих функций, т.е.
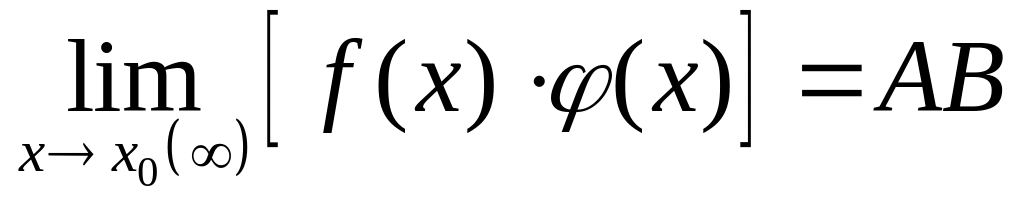 .
.Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е.
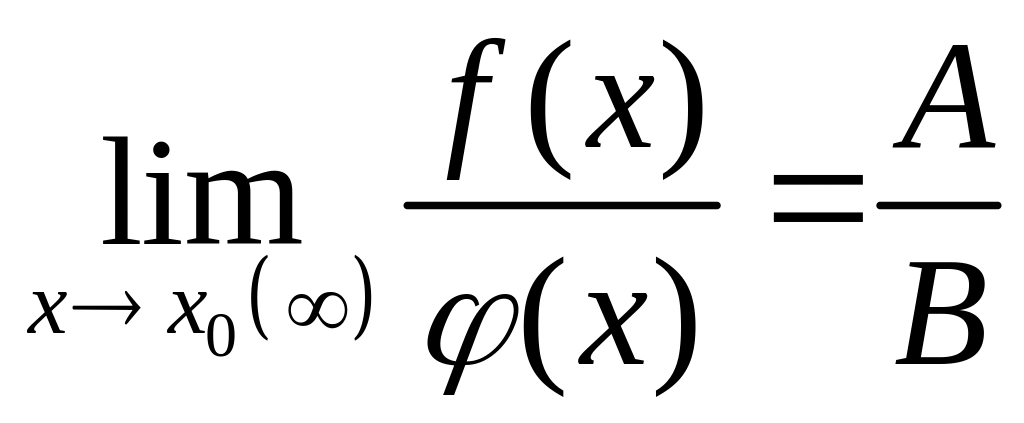
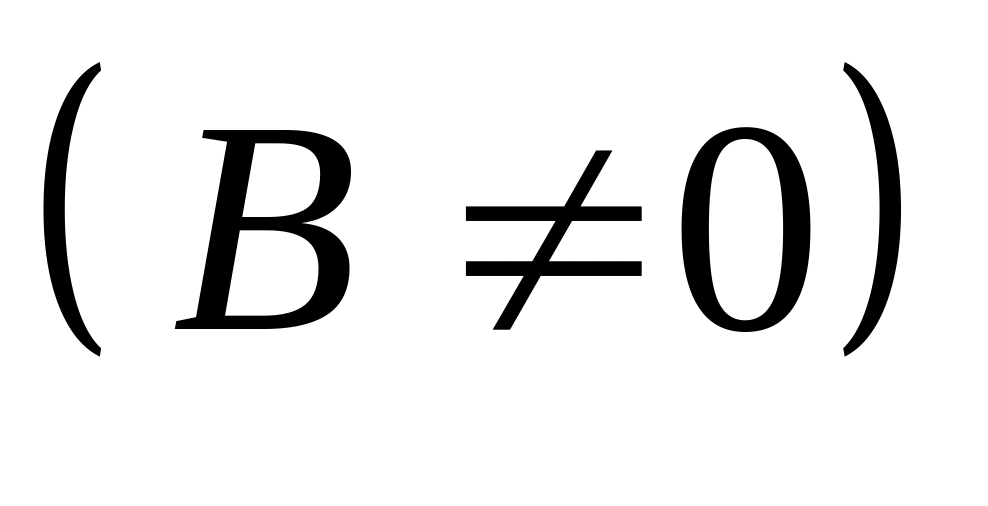 .
.Если
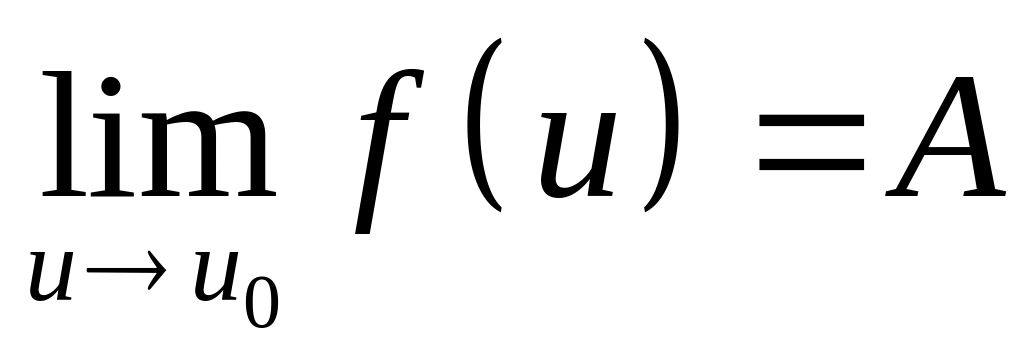 ,
,
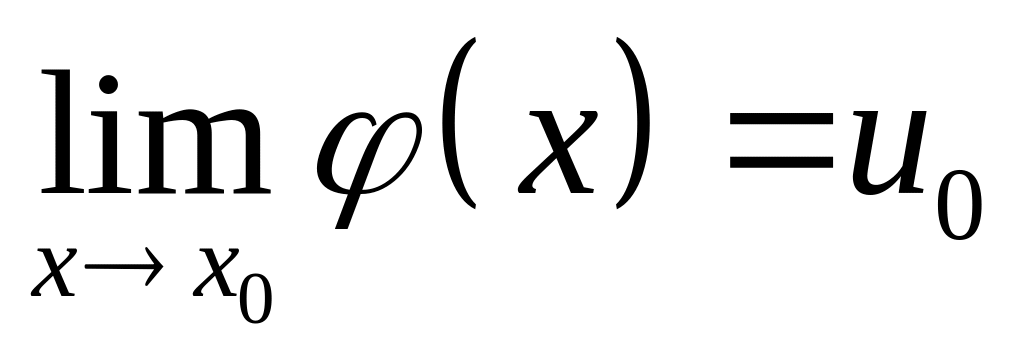 ,
то предел сложной функции
,
то предел сложной функции
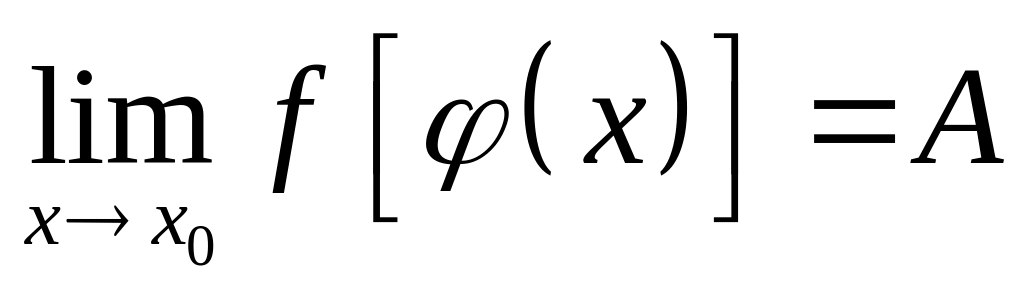 .
.Если в некоторой окрестности точки (или при достаточно больших )
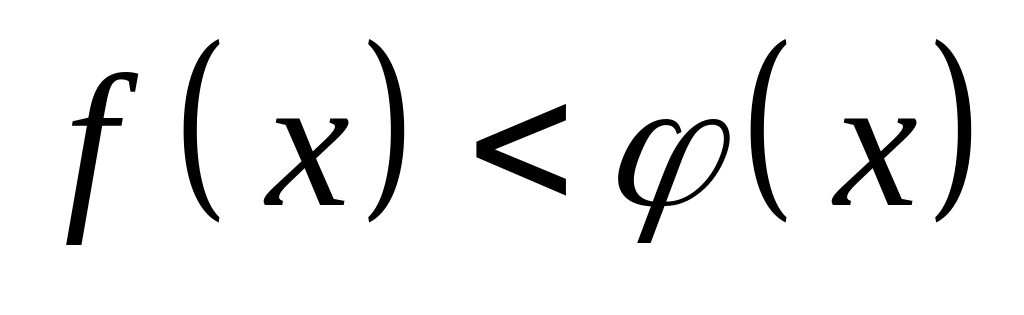 ,
то
,
то
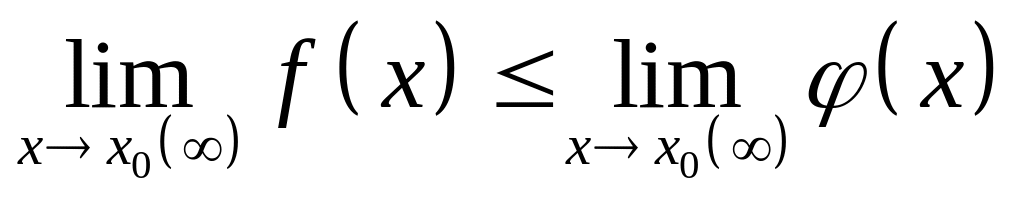 .
.
Пример.
Вычислить
![]() .
.
![]() .
.
8. Односторонние пределы. Несобственные пределы.
Если
значение функции
стремится к числу
![]() по мере стремления
к
со стороны меньших значений, то число
называют левосторонним пределом функции
в точке
по мере стремления
к
со стороны меньших значений, то число
называют левосторонним пределом функции
в точке
![]() и пишут
и пишут
![]() .
.
Если
значение функции
стремится к числу
![]() по мере стремления
к
со стороны больших значений, то число
называют правосторонним пределом
функции
в точке
и пишут
по мере стремления
к
со стороны больших значений, то число
называют правосторонним пределом
функции
в точке
и пишут
![]() .
.
Пример.
Вычислить
![]() .
.
Пусть
![]() .
Тогда при
.
Тогда при
![]() имеем:
имеем:
![]() - отрицательная бесконечно малая функция,
следовательно,
- отрицательная бесконечно малая функция,
следовательно,
![]() и
и
![]() ,
отсюда
,
отсюда
![]() .
.
Пусть
![]() .
Тогда при
.
Тогда при
![]() имеем:
- положительная бесконечно малая функция,
следовательно,
имеем:
- положительная бесконечно малая функция,
следовательно,
![]() и
и
![]() ,
отсюда
,
отсюда
![]() .
.
9. Непрерывность функции в точке.
Определение.
Функция
называется непрерывной в точке
,
если она удовлетворяет следующим трем
условиям: 1) определена в точке
(т.е. существует
![]() );
2) имеет конечный предел функции при
;
3) этот предел равен значению функции в
точке
,
т.е.
);
2) имеет конечный предел функции при
;
3) этот предел равен значению функции в
точке
,
т.е.
![]() .
.
Свойства функций, непрерывных в точке:
1. Если
функция
и
непрерывны в точке
,
то их сумма
![]() ,
произведение
,
произведение
![]() и частное
и частное
![]() (при условии
(при условии
![]() )
являются функциями, непрерывными в
точке
.
)
являются функциями, непрерывными в
точке
.
2. Если
функция
непрерывны в точке
и
![]() ,
то существует такая окрестность точки
,
в которой
,
то существует такая окрестность точки
,
в которой
![]() .
.
3. Если
функция
![]() непрерывны в точке
непрерывны в точке
![]() ,
а функция
,
а функция
![]() непрерывны в точке
непрерывны в точке
![]() ,
то сложная функция
,
то сложная функция
![]() непрерывна в точке
.
непрерывна в точке
.
Пример. Функция задана кусочно аналитически, различными аналитическими выражениями для различных подобластей изменения независимой переменной. Найти точки разрыва функции, если они существуют.
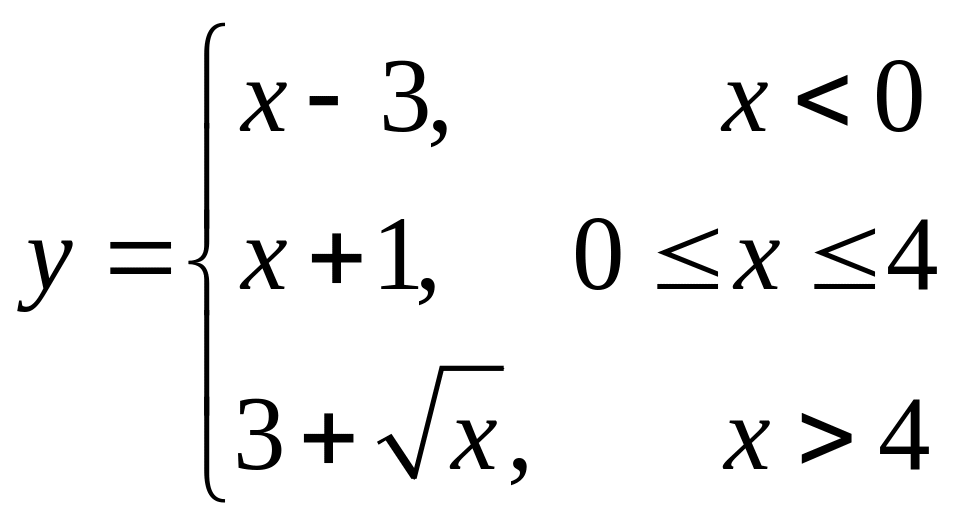
Так
как
![]() ,
и
,
и
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
то в точке
,
то в точке
![]() функция
не является непрерывной.
функция
не является непрерывной.
Так
как
![]() ,
и
,
и
![]() ,
,
![]() ,
т.е.
,
т.е.
![]() ,
то в точке
,
то в точке
![]() функция
непрерывна.
функция
непрерывна.
10. Непрерывность функции в интервале. Действия с непрерывными функциями.
Определение. Функция называется непрерывной на промежутке , если она непрерывна в каждой точке этого промежутка.
Свойства функций, непрерывных на отрезке:
1. Если
функция
непрерывна на отрезке
![]() ,
то она ограниченна на этом отрезке.
,
то она ограниченна на этом отрезке.
2. Если
функция
непрерывна на отрезке
,
то она достигает на этом отрезке
наименьшего значения
![]() и наибольшего значения
и наибольшего значения
![]() .
.
3. Если
функция
непрерывна на отрезке
и значение ее на концах отрезка
![]() и
и
![]() имеют противоположные знаки, то внутри
отрезка найдется точка
имеют противоположные знаки, то внутри
отрезка найдется точка
![]() такая, что
такая, что
![]() .
.
Пример. Доказать непрерывность функции .
Найдем![]() .
Так как
.
Так как
![]() ,
а
,
а
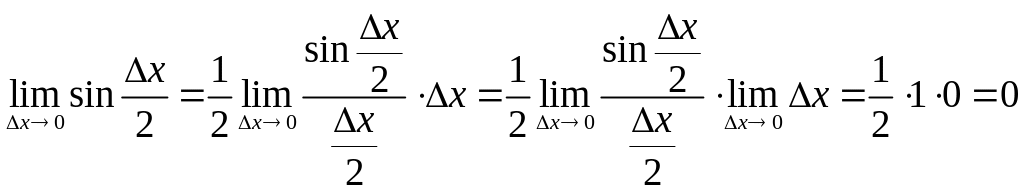 ,
т.е.
,
т.е.
![]() ,
то функция
является непрерывной на всей числовой
оси.
,
то функция
является непрерывной на всей числовой
оси.
