
- •1. Последовательности. Определение,
- •2.Предел последовательности. Сходимость.
- •3.Свойства сходящихся последовательностей.
- •4. Признаки сходимости последовательностей.
- •5.Определение функции. Способы задания функции.
- •6.Классификация основных элементарных функций.
- •7. Предел функции. Теоремы о пределах.
- •8. Односторонние пределы. Несобственные пределы.
- •9. Непрерывность функции в точке.
- •10. Непрерывность функции в интервале. Действия с непрерывными функциями.
- •11.Разрывы функций. Классификация разрывов.
- •12.Производная функции. Геометрическийс мысл производной.
- •13.Теоремы о производной суммы, произведения и частного.
- •14. Производная сложной и обратной функции.
- •15. Дифференциал, связь дифференциала и приращения функции.
- •16.Производные и дифференциалы высших порядков.
- •17.Производные основных элементарных функций.
- •18. Теорема Роля. Теорема Лагранжа.
- •19. Теорема Коши. Формула Тейлора и Маклорена.
- •20. Раскрытие неопределенности по правилу Лопиталя.
- •21.Экстремум функции, точки перегиба, асимптоты.
- •22. Правила исследования функций.
- •23. Определение функции нескольких переменных. Линии уровня.
- •24. Предел функции нескольких переменных.
- •25. Непрерывность функции нескольких переменных в точке и в области.
- •26. Дифференцирование функций нескольких переменных.
- •27. Частные производные высших порядков. Теорема об изменении порядка дифференцирования.
- •28.Сложная функция двух переменных ее производная.
- •29. Дифференциал функции двух переменных первого и высших порядков.
5.Определение функции. Способы задания функции.
Определение.
Если каждому элементу
множества
![]() ставится в соответствие вполне
определенный элемент
ставится в соответствие вполне
определенный элемент
![]() множества
множества
![]() ,
то говорят, что на множестве
задана функция
,
то говорят, что на множестве
задана функция
![]() .
.
Основные свойства функции:
Четность и нечетность. Функция называется четной, если для любых значений из области определения
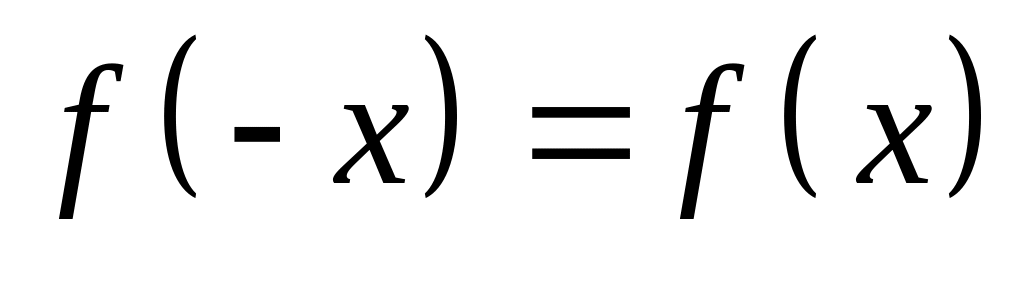 и нечетной, если
и нечетной, если
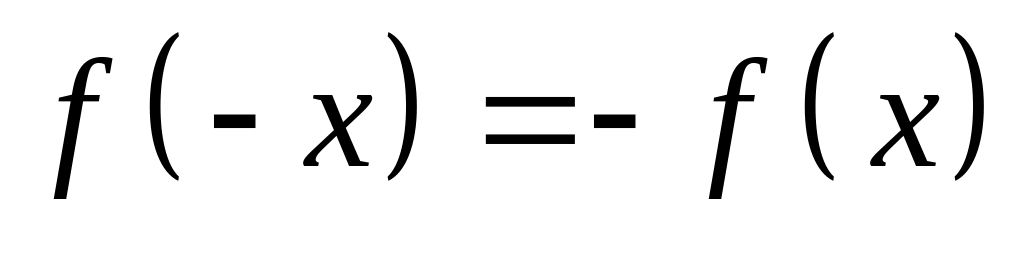 .
.Монотонность. Функция
 называется возрастающей (убывающей)
на промежутке
,
если большему значению аргумента из
этого промежутка соответствует большее
(меньшее) значение функции.
называется возрастающей (убывающей)
на промежутке
,
если большему значению аргумента из
этого промежутка соответствует большее
(меньшее) значение функции.Ограниченность. Функция называется ограниченной на промежутке , если существует такое положительное число
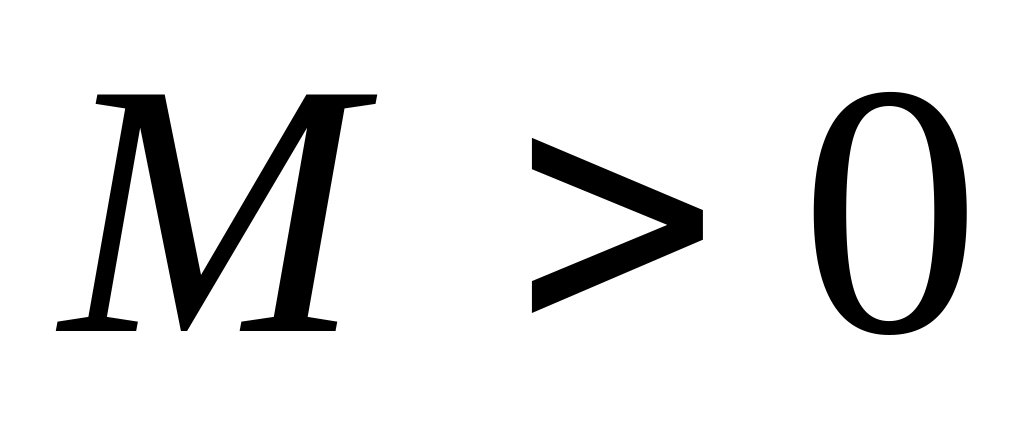 ,
что
,
что
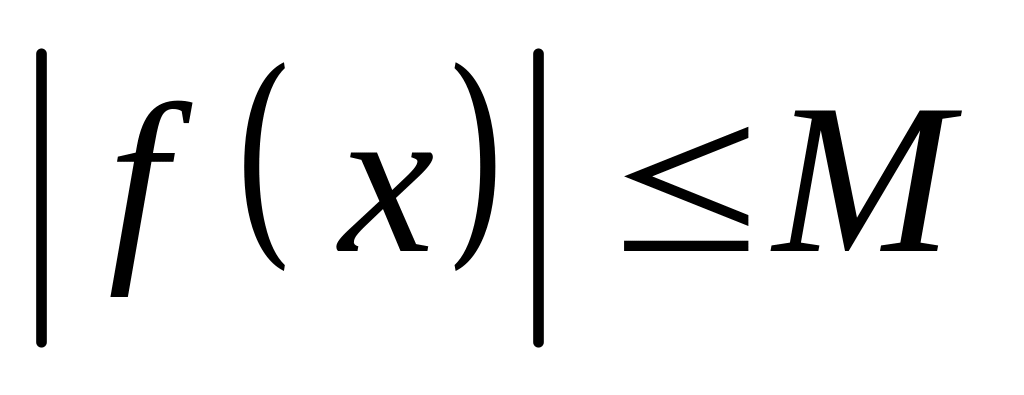 для любого
для любого
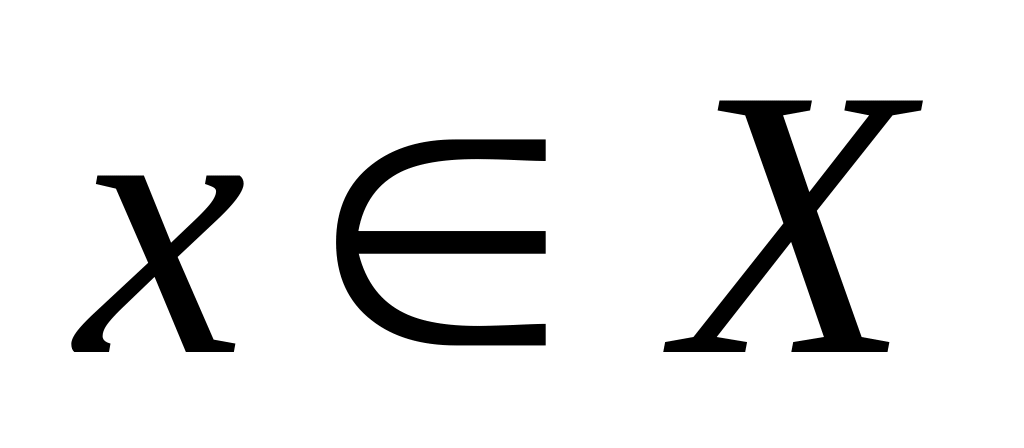 .
.Периодичность. Функция называется периодической с периодом
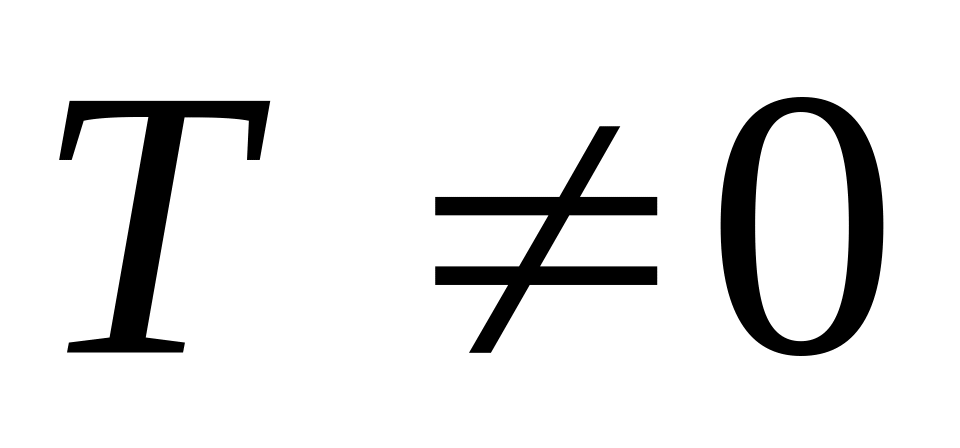 ,
если для любых
из области определения функции
,
если для любых
из области определения функции
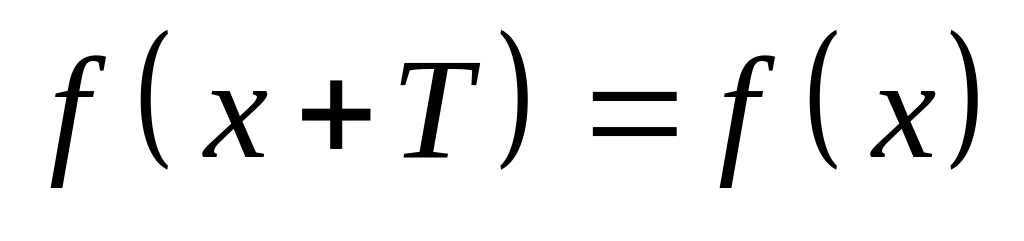 .
.
Способы задания функций:
1. Аналитический
способ, если функция задана формулой
вида
.
Функция
![]() задана аналитически.
задана аналитически.
2. Табличный способ состоит в том, что функция задается таблицей, содержащей значения аргумента и соответствующие значения функции .
|
-2 |
-1 |
0 |
1 |
2 |
|
4 |
1 |
0 |
1 |
4 |
3. Графический
способ состоит в изображении графика
функции – множества точек
![]() плоскости, абсциссы которых есть значения
аргумента
,
а ординаты – соответствующие им значения
функции
.
плоскости, абсциссы которых есть значения
аргумента
,
а ординаты – соответствующие им значения
функции
.
6.Классификация основных элементарных функций.
Основные элементарные функции:
Степенная функция:
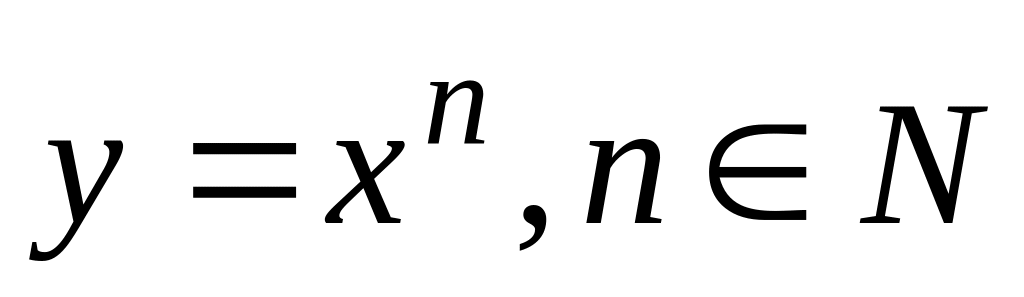 ,
,
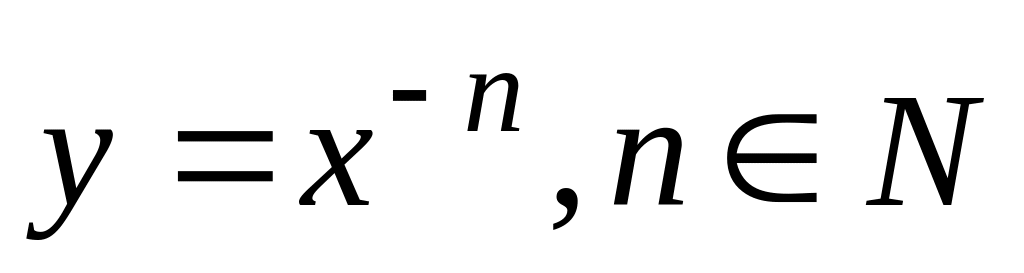 ,
,
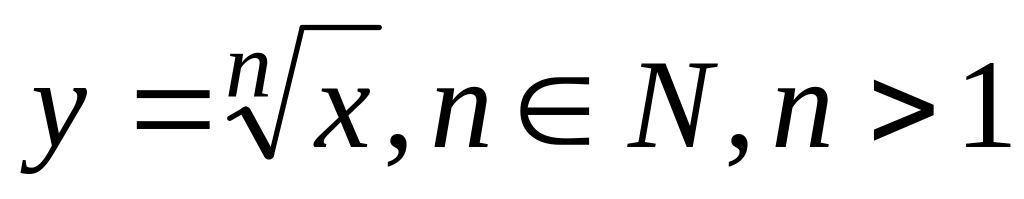 .
.Показательная функция:
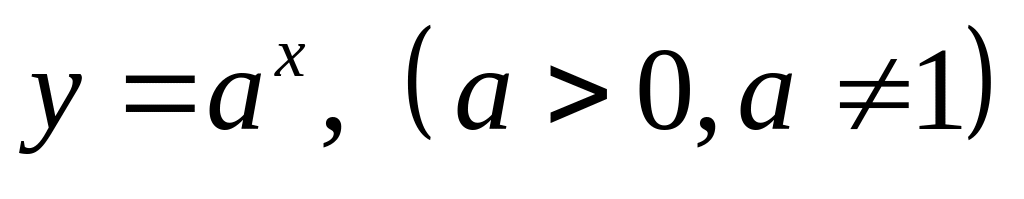 .
.Логарифмическая функция:
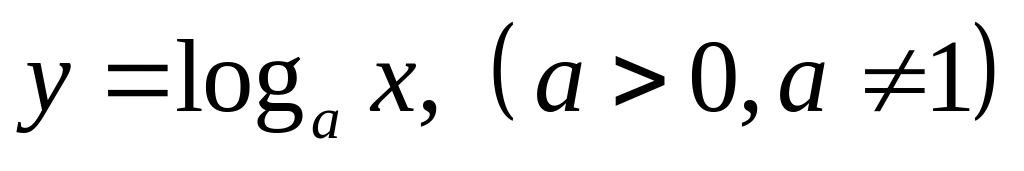 .
.Тригонометрические функции
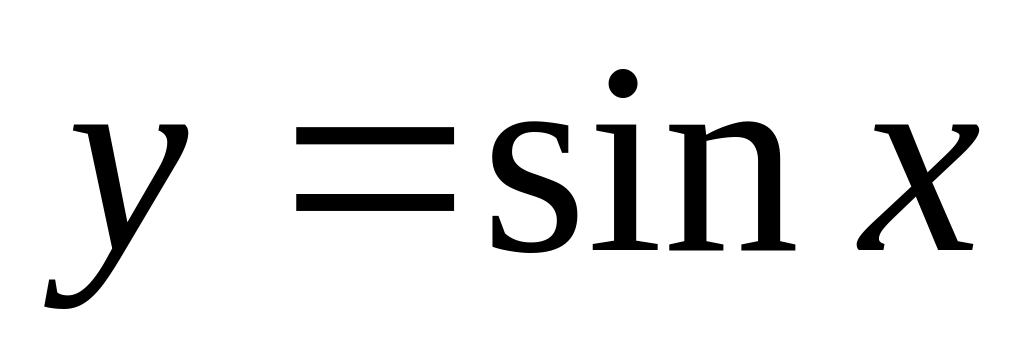 ,
,
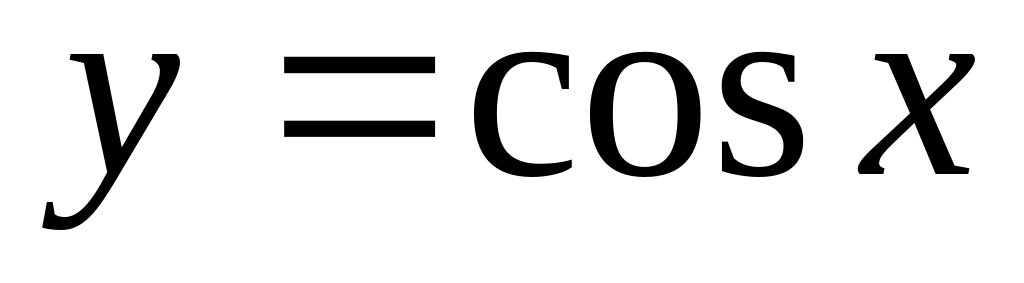 ,
,
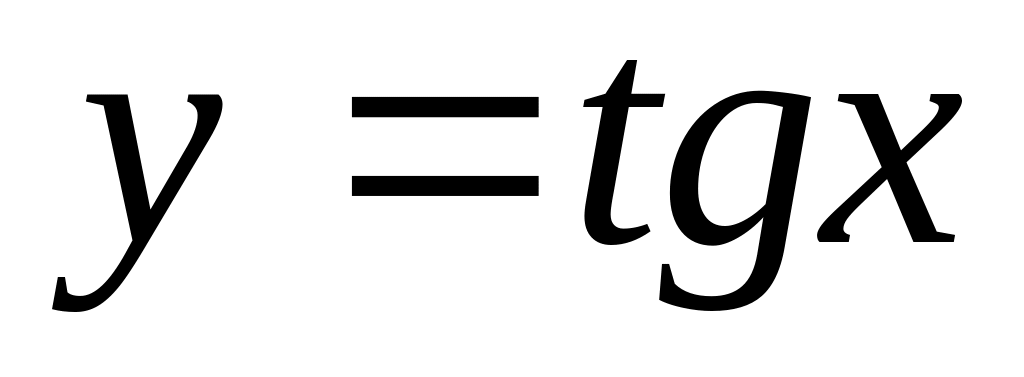 ,
,
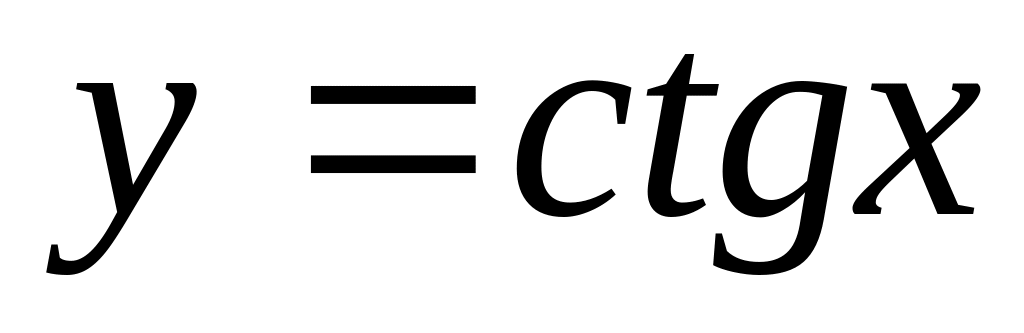 .
.Обратные тригонометрические функции:
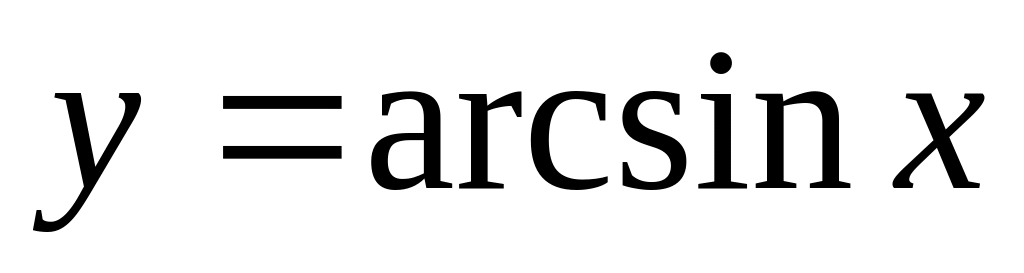 ,
,
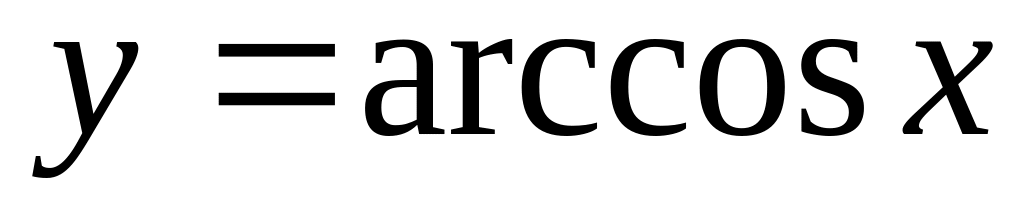 ,
,
 ,
,
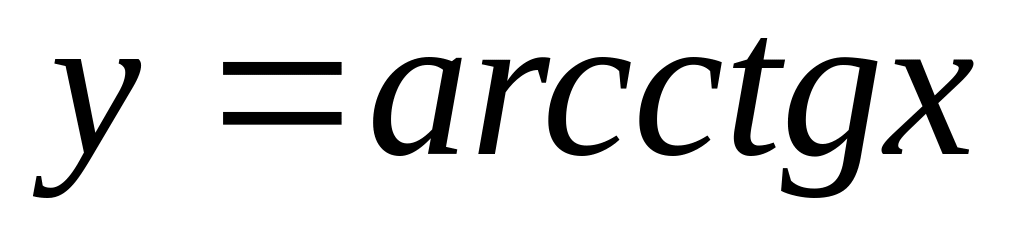 .
.
Классификация функций:
Алгебраические (целая рациональная функция, дробно-рациональная функция, иррациональная функция).
Неалгебраические (трансцендентные).
Преобразование графиков:
График
функции
![]() есть график функции
,
сдвинутый (при
есть график функции
,
сдвинутый (при
![]() влево, при
влево, при
![]() вправо) на
вправо) на
![]() единиц параллельно оси
единиц параллельно оси
![]() .
.
График функции
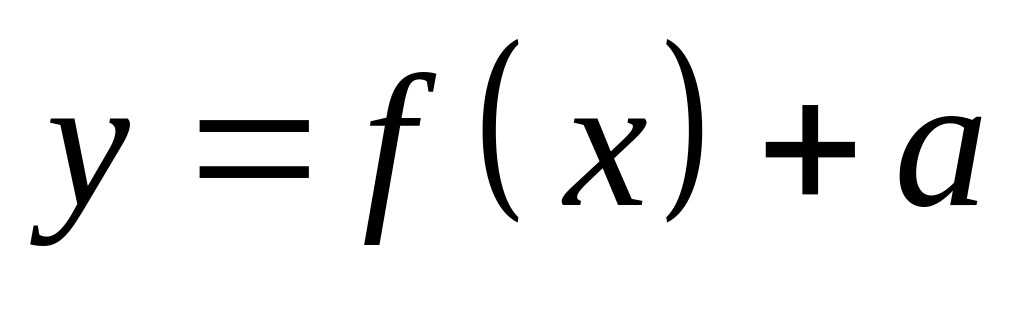 есть график функции
,
сдвинутый (при
вверх, при
вниз) на
единиц параллельно оси
есть график функции
,
сдвинутый (при
вверх, при
вниз) на
единиц параллельно оси
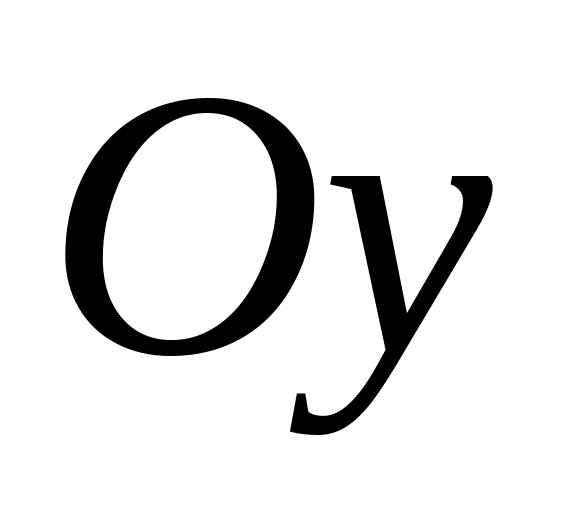 .
.График функции
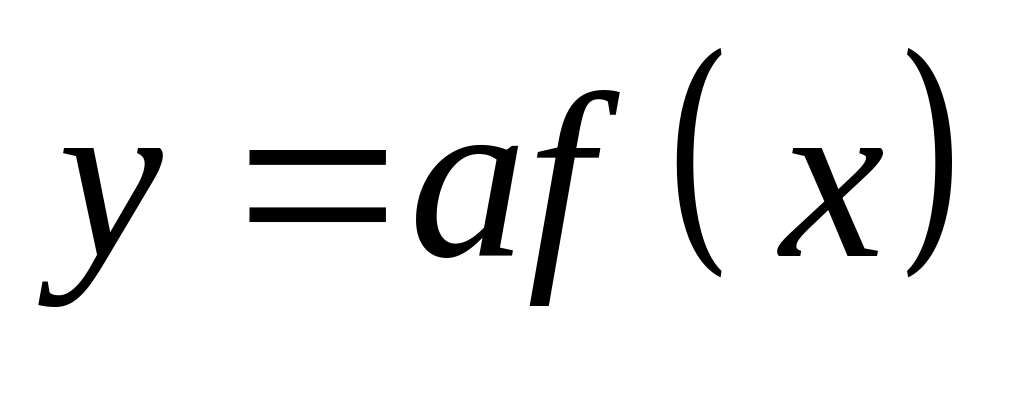 ,
,
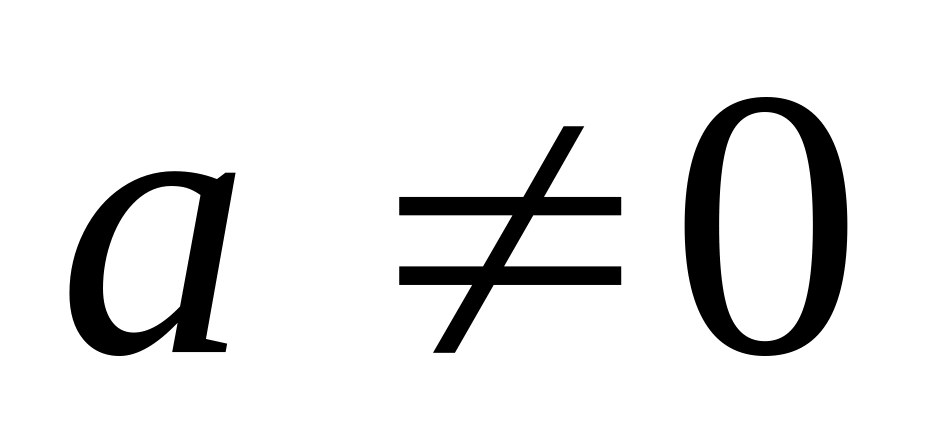 есть график функции
,
растянутый (при
есть график функции
,
растянутый (при
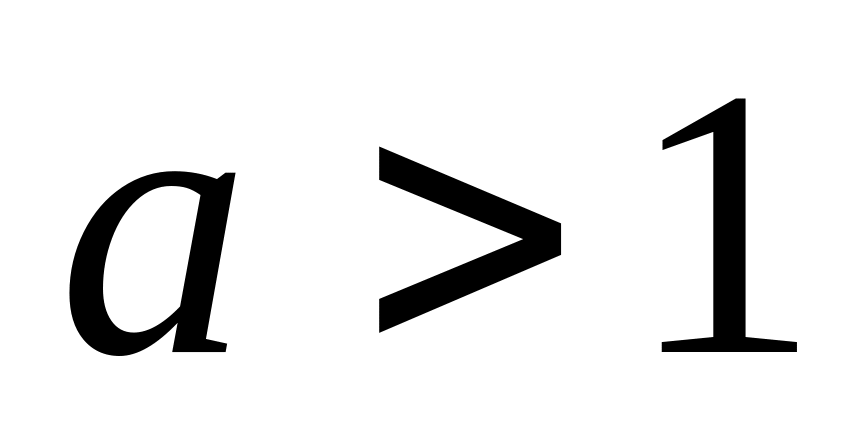 )
в
)
в
 раз или сжатый (при
раз или сжатый (при
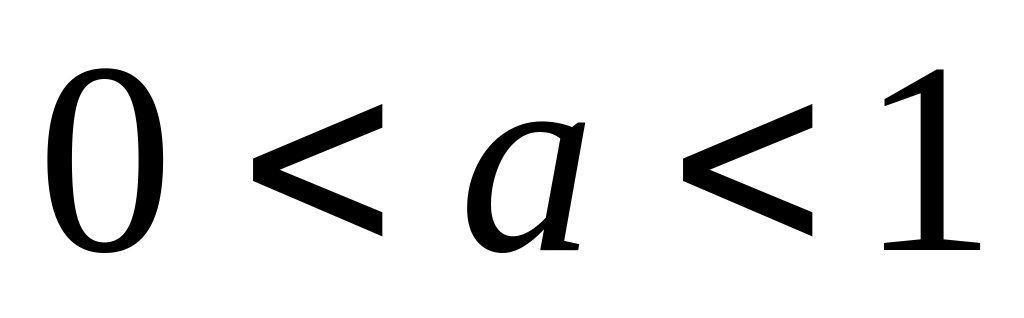 )
вдоль оси
.
)
вдоль оси
.График функции
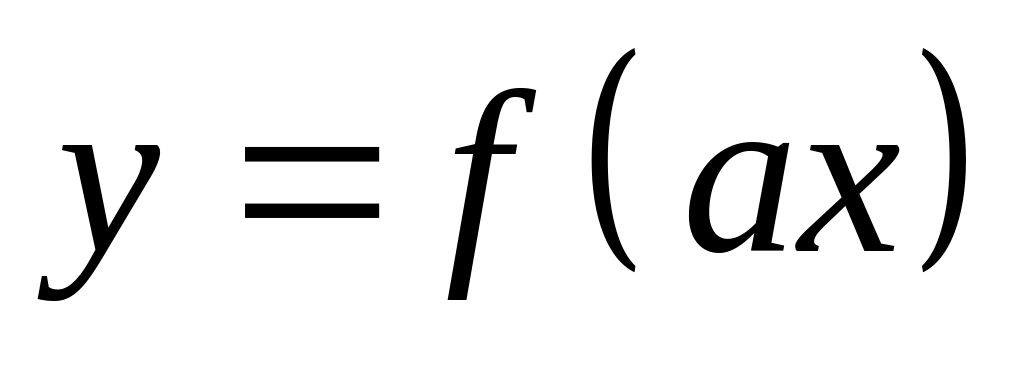 ,
есть график функции
,
сжатый (при
)
в
раз или растянутый (при
)
вдоль оси
.
,
есть график функции
,
сжатый (при
)
в
раз или растянутый (при
)
вдоль оси
.
4. Словесный
способ, если функция описывается правилом
ее составления. Например, функция
Дирихле:
![]() ,
если
- рационально;
,
если
- рационально;
![]() ,
если
- иррационально.
,
если
- иррационально.
Пример.
Построить график функции
![]() преобразованием графика функции
преобразованием графика функции
![]() или
или
![]() .
.
1. Строим график .
2. График
функции
![]() есть график функции
,
сжатый в 2 раза.
есть график функции
,
сжатый в 2 раза.
3. График
функции
![]() есть график функции
,
сдвинутый на
есть график функции
,
сдвинутый на
![]() влево.
влево.
4. График функции есть график функции , растянутый в 1,5 раза.
