
РГР [вариант 10]
.pdf
концы которого дают пределы интегрирования по y : -1 и 0. Из уравнений линий
выражаем x через y. Для y = − 4−x2 : x = ± 4−y2 , для y = 4−x2 − 2 : x = ± 4−( y+2)2 .
Т.к. рассматриваемые области находятся выше оси Ox, то в полученных зависимостях выбираем перед корнем знак "+".
−∫3 dx |
∫0 |
|
fdy + ∫0 |
|
dx ∫0 |
|
fdy = ∫0 |
|
4−( y+2)2 |
|
||
|
|
|
dy |
∫ |
|
fdx |
||||||
− |
|
2 |
− |
3 |
|
2 |
|
− |
|
|
2 |
|
2 |
− 4−x |
|
4−x |
|
−2 |
1 |
|
4−x |
|
|
||
|
|
|
|
|
|
|
|
|
||||

двух
разбивать
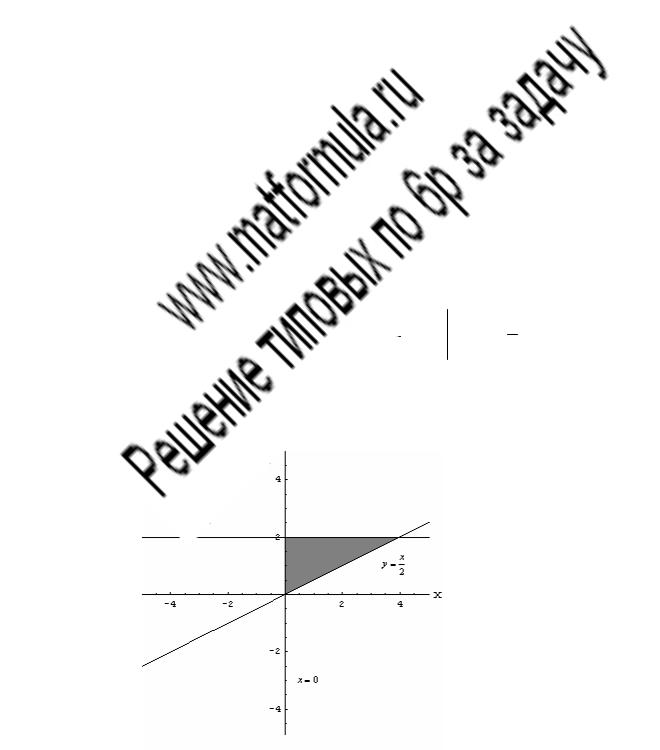
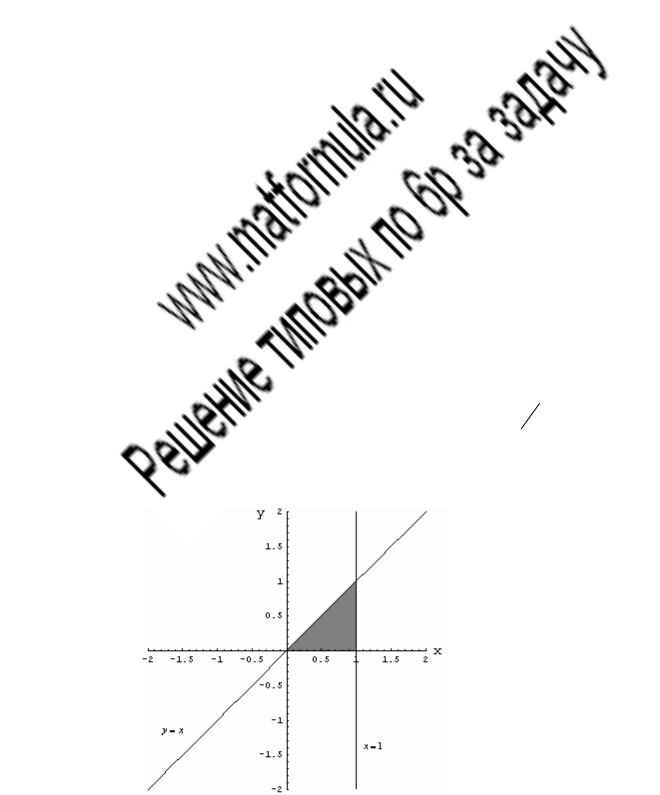
значит, пределы по x равны 0 и 1. Пределы интегрирования по y:y = −x2 . y = x.
∫∫(12xy +9x2 y2 )dxdy = ∫1 |
dx ∫x (12xy +9x2 y2 )dy = ∫1 |
dx(6xy2 +3x2 y3 ) |
|
x2 = |
|||||
|
|||||||||
D |
0 |
−x2 |
0 |
|
|
|
|
|
−x |
= ∫1 (6x2 +3x7 / 2 −6x5 +3x8 )dx = (2x3 + 2 |
3 x9 2 − x6 + 13 x9 ) |
|
1 |
= 2 |
|
|
|||
|
|
|
|||||||
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|||
= ∫2 8y(1 −e−y2 / 4 )dy = (4 y2 ) |
|
2 −(−16e−y2 / 4 |
) |
|
2 =16 −16 + |
16 |
= |
16 |
|
|
|||||||
|
||||||||
0 |
|
0 |
|
|
0 |
e |
|
e |
|
|
|||||||
|
|
|

|
|
|
|
|
|
|
|
|
|
|
0 yz |
|
|
|
|
|
|||
|
|
|
|
y |
|
||||
0 |
0 |
0 |
0 |
|
|
0 |
|||
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
y |
2 |
|
|
1 |
|
||
|
|
||||||||||
|
|
|
|||||||||
|
|
|
|
|
|||||||
= −2∫y2 |
|
|
(1 + y −ey )dy = 2∫(ey − y −1)dy = 2 ey − |
|
− y |
|
|
= 2e −5 |
|||
y |
2 |
|
|||||||||
2 |
|||||||||||
0 |
|
0 |
|
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
||||
∫∫∫ 15x +30z |
dx dy dz = ∫dx∫dy |
∫ |
15x +30z dz =15∫dx∫dy xz + z |
|
= |
V |
0 0 |
0 |
0 0 |
|
0 |
|
|||||
|
|
=15∫1 dx∫x (x4 + x3 +9 y4 +3xy2 +6x2 y2 )dy =15∫1 dx((x4 + x3 )y + 9 |
5 y5 + xy3 + 2x2 y3 ) |
|
x = |
|||
|
||||||
0 |
0 |
0 |
|
|
0 |
|
= ∫1 (30x4 +72x5 )dx = (6x5 +12x6 ) |
|
1 = 6 +12 =18 |
|
|
|
|
|
|
|
|
|||
0 |
|
|
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|

|
D |
|
|
|
1 |
|
|
3 |
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 x |
|||||||||
|
|
|
|
|
|
|
|
2 x |
|
|
|
|
|
|
|
|
|
|
x |
3 |
− |
3 |
|
|
9 |
3 |
−3ln 3 −1 = 26 −3ln 3 |
|
|
|
|
||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
||||||||||||
= |
|
2 |
ln x |
|
|
= 3 |
|
|
|
|
|||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

x = r cosϕ
y = r sin ϕ
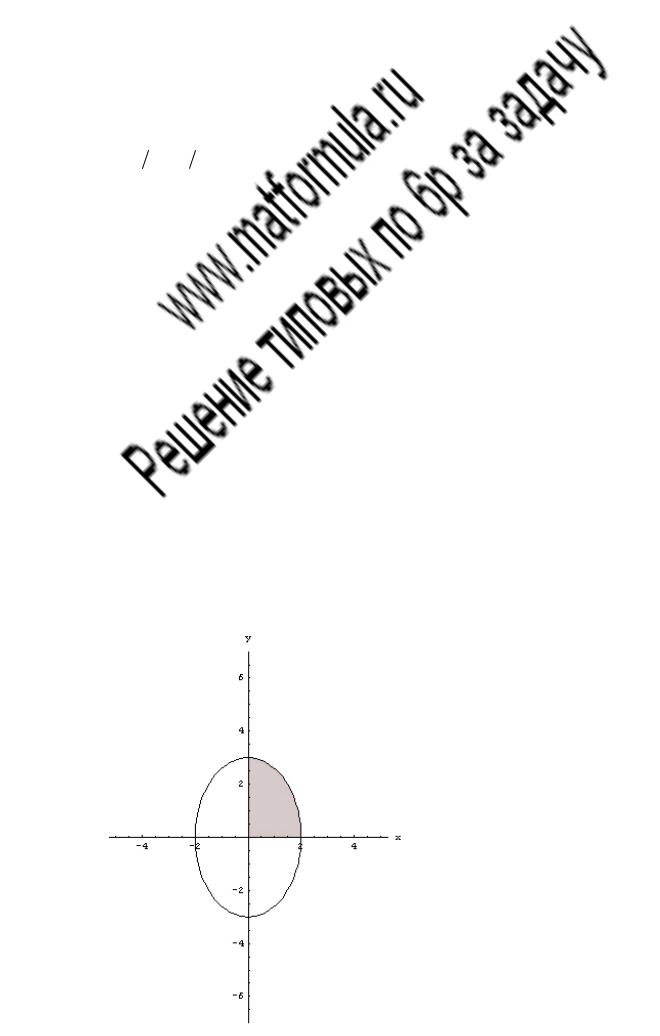
Окружность x2 −2x + y2 = 0 имеет полярное уравнение
r2 sin2 ϕ −4r cosϕ + r2 cos2 ϕ = 0. Откуда r = 4 cosϕ. Аналогично x2 −8x + y2 = 0 r2 sin2 ϕ −8r cosϕ + r2 cos2 ϕ = 0 r = 8cosϕ.
Прямая y = x |
3 |
имеет полярное уравнение r sin ϕ = r cosϕ |
. |
||||
|
|
|
|
|
3 |
|
|
Откуда tgϕ = |
1 |
3 |
ϕ =π |
6 |
. Аналогично |
|
|
|
|
|
|
|
|
||
y = x 3 r sinϕ = |
3r cosϕ tgϕ = 3 ϕ =π |
3 |
|
||||
|
|
|
|
|
|
|
|
Тогда площадь фигуры будет определяться по формуле: |
|
||||||
|
|
|
|
|
π / 3 |
|
4 cos ϕ |
π / 3 |
|
r |
2 |
|
|||
S = ∫∫dxdy = |
∫ dϕ |
∫ rdr = |
∫ |
dϕ |
|
|
|||||||||
2 |
|||||||||||||||
|
D |
|
|
|
π / 6 |
|
2 cos ϕ |
π / 6 |
|
|
|||||
|
3ϕ |
+ |
3 |
|
|
|
π 3 |
= |
π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
= |
2 |
sin 2ϕ |
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
π 6 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
4 cos ϕ
= π∫/ 3 6 cos2 ϕdϕ =
2 cos ϕ |
π / 6 |
|

MD = ∫∫μ(x, y)dxdy = |
0 |
3 |
r (cosϕ −sin ϕ) |
|
0 |
(cosϕ −sin ϕ)dϕ(r) |
|
3 |
|
||||
|
|
|
|||||||||||
∫ |
dϕ∫ |
|
|
|
|
|
rdr = |
∫ |
|
|
= |
||
r |
2 |
|
|
|
|
1 |
|||||||
D |
−π / 2 |
1 |
|
|
|
|
|
−π / 2 |
|
|
|
|
|
= 2 ∫0 (cosϕ −sin ϕ)dϕ = 2 (sin ϕ +cosϕ) |
|
0−π |
= 4 |
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||||
−π / 2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 cosϕ |
|
−2r sin ϕ |
|
|
|
|
|
|
|
|
|
|||
|
|
∂ϕ |
|
∂r |
|
= |
|
|
|
= 6r |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∂y |
|
|
∂y |
|
|
3sin ϕ |
|
|
3r cosϕ |
|
|
|
|
|
|
|
|
|
|||||
|
|
∂ϕ |
|
∂r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(1) |
π / 2 |
1 |
|
|
|
|
|
|
|
|
|
||
m = ∫∫m(x, y) dx dy |
= |
|
∫ |
dϕ∫6r 8r3 cos3 ϕ 3r sin ϕdr = |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
D |
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
|
π |
/ 2 |
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
r |
6 |
1 |
|
|
||
= |
∫ |
cos3 ϕ sinϕ dϕ ∫144 r5 |
|
dr = −∫cos3 ϕ d(cosϕ) 144 |
|
|
| |
|
= |
||||||||||||||||
|
|
|
|||||||||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
6 |
0 |
|
||||
|
|
|
|
|
|
cos4 ϕ |
π |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
− |
2 |
|
24 = |
24 = 6 |
|
|
|
|
|
|
|
|
|
||||||||||
|
4 |
|
|
| |
|
4 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
9 |
|
|
|
|
x |
|
|
|
25 |
9 |
|
|
|
|
x x |
|
|
= |
|
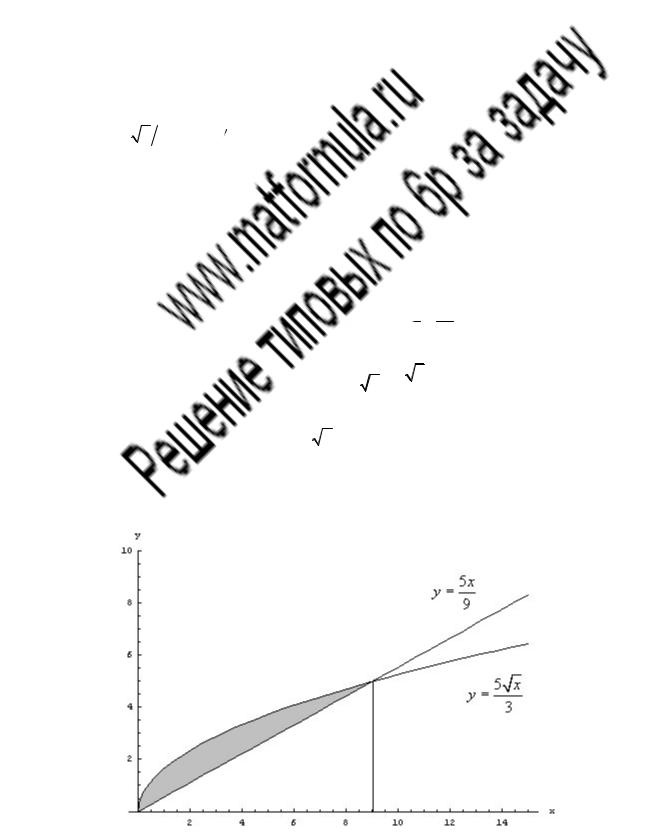
∫(3 + |
x ) |
x − |
|
dx |
= |
|
∫ |
3 |
x − |
|
|
dx = |
|||||
27 |
3 |
27 |
3 |
|
|||||||||||||||
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
|
25 |
|
|
|
2x2 |
x 9 |
|
50 |
|
|
|
|
|
x 9 |
|
|
|
||
= |
|
|
2x x − |
|
| |
= |
|
x x 1 |
− |
|
| |
= 20 |
|
||||||
|
|
|
|
|
|||||||||||||||
|
27 |
|
|
|
15 |
0 |
|
27 |
|
|
|
|
|
15 0 |
|
|
|
||
