25. Виды средних величин, способы их вычисления.

Следующие виды средних величин широко применяются на практике:

-средняя арифметическая

-средняя гармоническая

-средняя геометрическая

-средняя квадратическая

-средняя кубическая

Перечислим сведения, объединяющиеся в общей формуле степенной средней:

-средняя хронологическая

-средняя групповая (частная)

-средняя многомерная

-средняя системная

-средняя прогрессивная

-средняя скользящая

-средняя экспоненциальная

-средние структурные: мода, медиана

Таким образом, средняя величина может быть вычислена по-разному. Выбор способа вычисления средней величины обусловлен:

-назначение средней

-сущностью усредняемых признаков

-характеристикой исходных данных

Средние величины подразделяются на:

-общие средние величины

-групповые (частные средние)

Средние величины имеют 2 формы:

-простую (невзвешенную)

-взвешенную

26. И 27. Средняя арифметическая простая и взвешенная. Условия её применения.

Средняя арифметическая простая (невзвешенная) вычисляется по след. формуле:

n

Х =∑х / n или Х =∑х / n

I=1

Х – индивидуальное значение признаков, т.е. варианты

n – количество единиц в изучаемой совокупности

Х = (Х1+Х2+Х3+…+Хn) / n

Средняя арифметическая простая используется в тех случаях, когда расчёт осуществляется по несгруппированным данным, т.е. когда варианты встречаются по 1 разу и имеют одинаковый вес в совокупности.

Средняя арифметическая взвешенная вычисляется:

Х = ∑хf / ∑f

f – количество единиц в данной совокупности. Частота или вес.

Х= (x1f1+x2f2+x3f3+…+xnfn) / f1+f2+f3+…+fn

Средняя арифметическая взвешенная применяется тогда, когда отдельные значения осредняемого признака могут повторяться, встречаться несколько раз.

Таким образом при вычислении средней арифметической взвешенной варианты имеют различный вес в совокупности. Расчёт средней производится по сгруппированным данным, т.е. вариационным рядам, которые могут быть дискретными или интервальными.

На практике определить среднюю можно через исходное соотношение средней (ИСС). Расчёт средней производится через логическую формулу, т.е. необходимо исходить из экономического содержания исчисляемых показателей.

ИСС = суммарное значение осредняемого признака / число единиц совокупности

28. Вычисление средней арифметической по данным вариационного

интервального ряда распределения.

Интервальный ряд – это ряд, в котором варианты заданы в пределах «от» и «до».

При расчете средней по интервальному вариационному ряду необходимо от интервалов к их серединам, т.е. интервальный ряд необходимо преобразовать в дискретный.

Середина (центр) интервала определяется 2-мя способами:

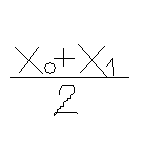
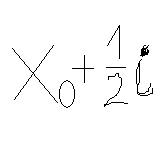, где i – величина интервала;

х0 - нижняя граница интервалов; х1 - верхняя граница интервалов

i = x1-x0

После преобразования интервального ряда в дискретный расчёты производятся по формуле средней арифметической взвешенной