Расчет двухуровневого "дерева" решений

Пример 3.6. Рассмотрим ситуацию более сложную, чем в предыдущем примере, а именно: банк решает вопрос, проверять ли конкурентоспособность клиента перед тем, как выдавать заем. Аудиторская фирма берет с банка 80 ф. ст. за каждую проверку. В результате этого перед банком встают две проблемы: первая — проводить или нет проверку, вторая — выдавать после этого заем или нет.

Решая первую проблему, банк проверяет правильность выдаваемых аудитор­ской фирмой сведений. Для этого выбираются 1000 человек, которые были проверены и которым впоследствии выдавались ссуды:

Таблица 3.24. Рекомендация аудиторской фирмы и возврат ссуды

Рекомендации после проверки кредитоспособности	Фактический результат
	Клиент ссуду вернул	Клиент ссуду не вернул	Всего
Давать ссуду Не давать ссуду	735 225	15 25	750 250
Всего	960	40	1000

Какое решение должен принять банк?

Решение.

Этап 1. Построим "дерево", как показано ниже. Вероятности проставляются по данным этапа 2.

Этап 2. Используя данные табл. 3.24, вычислим вероятность каждого исхода:

Р (клиент ссуду вернет; фирма рекомендовала) = 7,35/750 = 0,98;

Р (клиент ссуду не вернет; фирма рекомендовала) = 15/750 = 0,02;

Р (клиент ссуду вернет; фирма не рекомендовала) = 225/250 = 0,9;

Р (клиент ссуду не вернет; фирма не рекомендовала)= 25/250= 0,1.

Этап 3. На этом этапе слева направо проставим денежные исходы каждого из "узлов", используя конечные результаты, вычисленные ранее. Любые встречаю­щиеся расходы вычитаем из ожидаемых доходов. Таким образом, подсчитываем все "дерево", опираясь на ранее полученные результаты. После того, как пройдены квадраты "решений", выбирается "ветвь", ведущая к наибольшему из возможных при данном решении ожидаемому доходу. Другая "ветвь" зачеркивается, а ожи­даемый доход проставляется над квадратом решения.

Сначала посмотрим на кружки исходов В и С, являющиеся следствием квад­рата 2 (выдавать ли заем клиенту?)

Доход, ожидаемый от исхода В:

Е (В) = 17250 ф. ст. * 0,98 + 0 * 0,02 = 16905 ф. ст.,

чистый ожидаемый доход:

NE (В) = 16905 - 15000 = 1905 ф. ст.

Доход, ожидаемый от исхода С:

Е (С) = 16350 ф. ст. х 1,0 = 16350 ф. ст.,

чистый ожидаемый доход:

NE (С) = 16350 - 15000 = 1350 ф. ст.

Принятие решений в условиях определенности

Задачи линейного программирования

Инструментом моделирования распределения ресурсов для достижения цели чаще всего являются методы линейного программирования.

Задача линейного программирования является частным случаем задачи оптимизации и записывается в следующем виде:

Задачу линейного программирования можно решать графическими и аналитическими методами. Одним из самых известных аналитических методов по праву считается симплекс-метод, который реализован в Excel (симплексом тела в k-мерном пространстве называют совокупность k+1 его вершин). Алгоритм симплекс-метода обеспечивает переход от одной вершины к другой в таком направлении, при котором значение целевой функции от вершины к вершине улучшается. Поэтому и аналитический метод, основанный на итерациях вычисления целевой функции и переменных в вершинах, с учетом этого получил свое название.

Рассмотрим сам метод, его реализацию в Excel и, самое главное, анализ результатов с целью принятия решений на примере, приведенном в книге³ задачи распределения ресурсов.

Задача. Требуется определить, в каком количестве надо выпускать продукцию типов Прод1, Прод2, Прод3, Прод4 с целью получения наибольшей прибыли. Известно, что для изготовления требуются ресурсы трех видов: трудовые, сырье, финансы. Количество каждого ресурса на момент решения задачи, норма расхода каждого вида ресурса на единицу продукции каждого типа и прибыль от реализации единицы продукции известны и приведены в таблице на рис. 1.

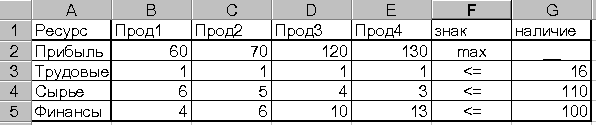
Рис.1

Введем обозначения:

x_j – количество выпускаемой продукции j-го типа (j= 1…4);

b_i – количество наличного ресурса i-го вида (i= 1…3);

a_ij – норма расхода i-го ресурса для выпуска единицы продукции j-го типа;

c_j – прибыль, получаемая от реализации единицы продукции j-го типа.

Математическая модель задачи имеет вид:

F == 60x₁ +70x₂ + 120x₃ +130x₄ Þ max

x₁ + x₂ + x₃ + x₄ <= 16

6x₁ +5x₂ +4x₃ + 3x₄ <= 110

4x₁ + 6x₂ +10x₃ + 13x₄ <= 100

x_ij >=0, j = 1…4

Вычисление всех искомых значений обеспечивает Excel с помощью надстройки Сервис–Поиск решения.