2.1. Плоская стенка с прямыми ребрами постоянного поперечного сечения

Основные параметры ребристой стенки (рис. 2.1): l, h, –длина высота, толщина ребра; П=2(l+ )–периметр ребра; f=l –площади сечения ребра; b–шаг ребер; В, –ширина и толщина плоской стенки; –температуры сред, окружающих стенку, , – коэффициенты теплоотдачи от поверхности ребра и от гладкой поверхности стенки к окружающей среде; температуры ребра у основания и на его конце.

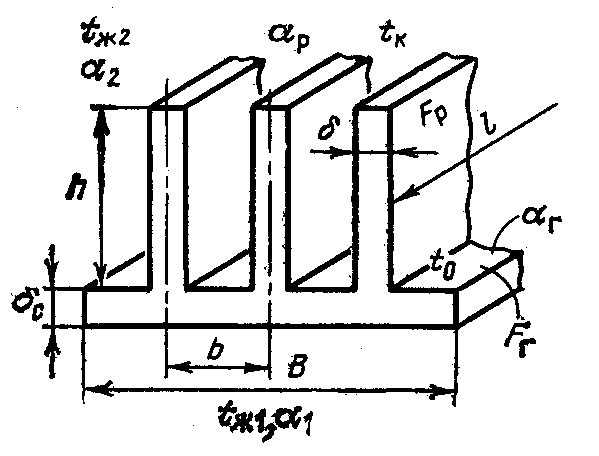
Рис. 2.1. Плоская ребристая стен­ка

При расчете теплоотдачи с поверхности одного прямого ребра в окружающую среду, имеющую температуру , тепловой поток , Вт, определяется nо формуле

(2.1)

где –избыточная температура у основания ребра, К; –параметр. ; th(mh)= –тангенс гиперболический; – теплопроводность материала ребра Вт/(мК).

Тепловой поток Qr, Вт, с гладкой поверхности Fr стенки в промежутках между ребрами

(2.2)

где п –количество ребер на 1 м ширины стенки; l–длина стенки (длина ребра), м.

Суммарный тепловой поток Qo при теплоотдаче с оребренной по­верхности стенки

(2.3)

Тепловой поток, обусловленный теплопередачей между двумя сре­дами, разделенными плоской стенкой, имеющей оребрение с одной сто­роны,

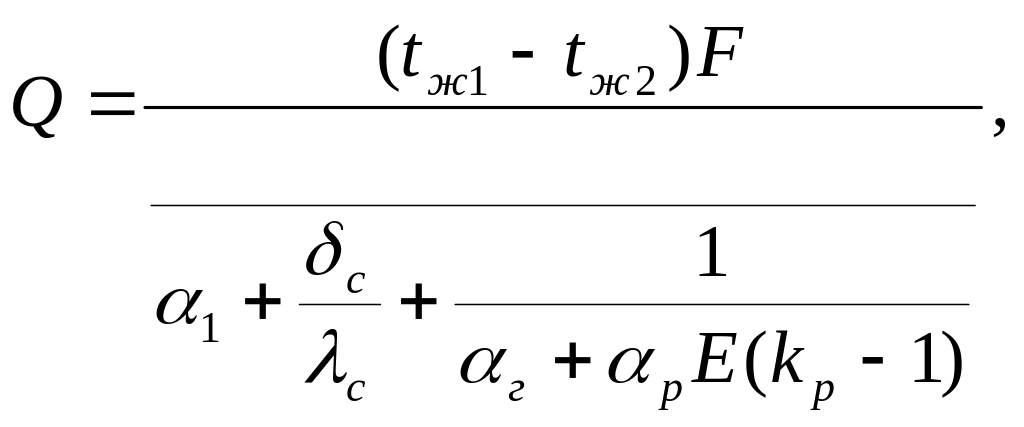(2.4)

где F–площадь неоребренной поверхности стенки, м²; –коэффи­циент теплоотдачи на неоребренной поверхности стенки, Вт/( К); –теплопроводность материала стенки, Вт/(м·К); Е–коэффициент эффективности ребра; k_p–коэффициент оребрения.

Коэффициент эффективности ребра Е является его рабочейхарактеристикой и представляет собой отношение теплового потока, действительно рассеиваемого ребром в окружающую среду, к тепловому потоку который ребро могло бы отдать, если бы вся его поверхность находилась при температуре :

(2.5)

или, пренебрегая теплоотдачей с торца ребра,

(2.5a)

где –средняя температура поверхности ребра.

Повышения теплосъема ребра можно добиться при уменьшении mh..

Коэффициент оребрения

(2.6)

где – суммарная площадь оребренной поверхности стенки, м².

В формуле (2.4) можно положить , тогда тепловой по­при теплопередаче через оребренную стенку

(2.7)

а коэффициент эффективности тонкого ребра (в предположении, что и П==2l) можно определить из зависимости

(2.8)

где , или из графика рис.2.2.

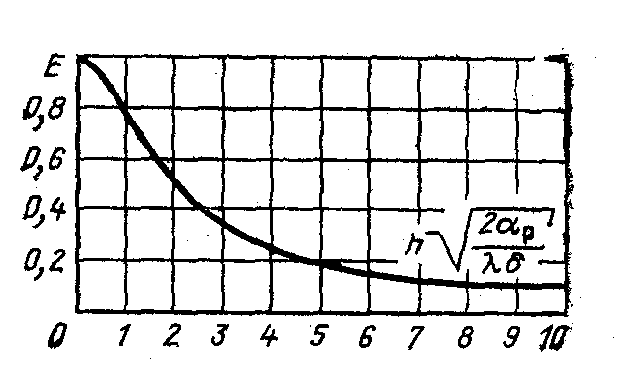
Рис. 2.2. Коэффициент эффективности Е ребра

Для учета теплоотдачи с торцевой поверхности ребра необходимо зысоту ребра h увеличить на 0,5 .

Температура на конце ребра

или (2.9)

где – избыточные температуры на конце ребра и у его осно­вания, К; ch(mh) =0,5 ( ) –косинус гиперболический.

2.2. Цилиндрическая стенка с круглым ребром постоянной толщины

Расчет теплопередачи через трубу, оребренную снаружи кольцевыми ребрами (рис. 2.3), можно проводить по формулам (2.7) и (2.8) принимая h=R–r и умножая коэффициент эффективности Е на поправочный коэффициент , который определяется по графику рис.(2,1)

Коэффициент эффективности круглого ребра

(2.1)

где – коэффициент, определяемый по графику рис. 2.4 в зависимости от и R/r; - эффективная высота ребра, –отношение избыточных температур на конце у основания ребра.

Параметр m определяется из выражения

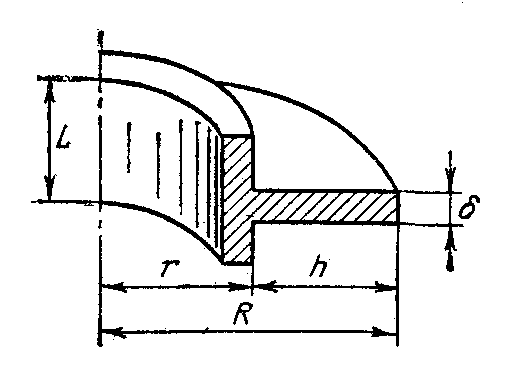
Рис. 2.3. Круглое ребро постоянной толщины

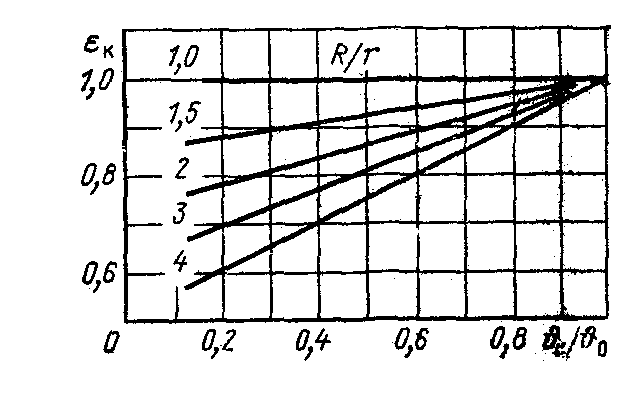
Рис. 2.4. Зависимость ε_к=f(ϑ_к/ϑ₀; R/r) для круглого ребра

Глава третья

ТЕПЛООБМЕН С УЧЕТОМ ВНУТРЕННИХ ИСТОЧНИКОВ

ТЕПЛОТЫ

B определенных условиях в телах могут происходить процессы выделением (поглощением) теплоты, например джоулево нагревание электропроводника, химические экзо- и эндотермические реакции, ядерные процессы в тепловыделяющих элементах (твэлах) реактора и т. п. |и процессы характеризуются мощностью внутренних источников теплоты или интенсивностью объемного тепловыделения , Вт/м³.

3.1. Однородная неограниченная пластина

Для плоской пластины ( =const), равномерно охлаждаемой обеих сторон (рис. 3.1), задана температура поверхности .

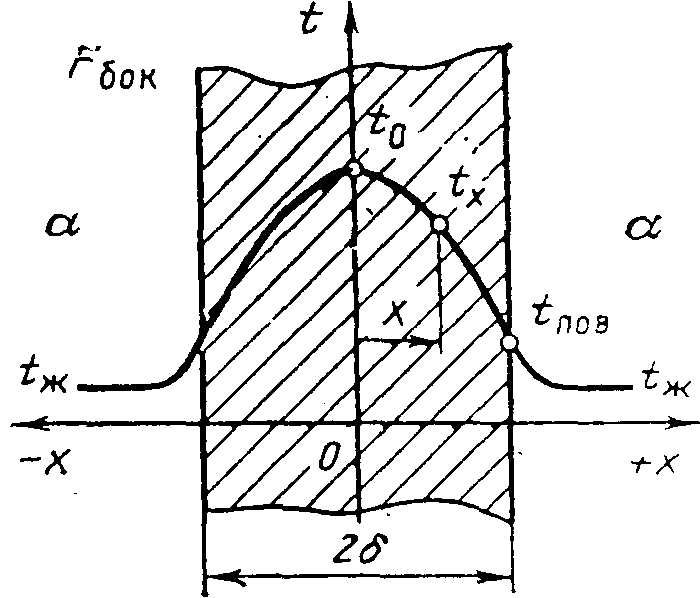
Рис. 3.1. Температурный гра­фик в пластине с учетом внут­ренних источников теплоты

Одномерное температурное поле пластине толщиной 2

(3.1)

где

В формуле (3.1) при х=0 температура в середине толщины пластины

(3.2)

Учитывая зависимость в условиях больших перепадов температур, температурное поле в пластине можно рассчитать по формуле

(3.3)

Для плоской пластины ( =const), равномерно охлаждаемой с обеих сторон, заданы температура среды и коэффициент теплоотдачи а.

Одномерное температурное поле в пластине

(3.4)

где

В формуле (3.4):

при х= температура на поверхности пластины

(3.5)

при х=0 температура в середине толщины пластины

(3.6)

Мощность внутренних источников теплоты для пластины опреде| ляется по формулам

(3.7)

(3.8)

(3.9)

Связь между объемной и поверхностной плотностями тепло выделения используется при определении теплового потока на боко вых поверхностях пластины

(3.10)

3.2. Цилиндрический стержень

Для бесконечного стержня ( =const) задана температура на оси .

Температурное поле в стержне диаметром

(3.11)

В формуле (3.8) при температура на поверхности стержня

(3.12)

С учетом зависимости температурное поле в стержне

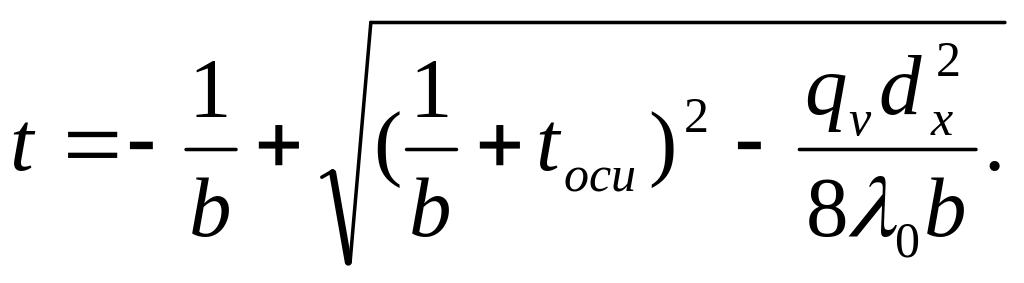(3.13)

Для стержня ( =const), равномерно охлаждаемого средой, заданы ее температура и коэффициент теплоотдачи а.

Температурное поле в стержне

(3.14)

В формуле (3.14):

при температура на оси стержня

(3.15)

температура на поверхности стержня

(3.16)

Мощность внутренних источников теплоты для стержня

(3.17)

(3.18)

(3.19)