16. Середні величини, види середніх величин.

Середні величини – це узагальнююча міра ознаки, що варіює у статистичній сукупності. Це узагальнюючий показник, який характеризує типовий рівень ознаки, що варіює, в розрахунку на одиницю сукупності.

Умови наукового використання середніх величин:

Якісна однорідна сукупність;

Сукупність має бути достатньо великою;

Використання загальних середніх з груповими

Призначення середніх в економічній галузі:

Характер рівня масових суспільних явищ;

Проведення порівняльного аналізу;

Вивчення тенденцій розвитку явищ;

Вибіркове спостереження;

Вимірювання взаємозв»язків

Види середніх величин:

середня арифметична;

середня гармонійна;

середня геометрична;

середня квадратична;

середня хронологічна.

Залежно від характеру первинної інформації:

проста – розраховується за не згрупованими даними;

зважена – розраховується за згрупованими даними.

За первинними не згрупованими даними обчислюється середньо-арифметична проста:

=

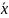У великих за обсягом сукупностях окремі значення ознаки можуть повторюватися. У такому разі їх можна об»єднати в групи а обсяг значень ознаки можна визначити як суму добутків варіант на відповідні їм частоти. Такий процес називають зважуванням, а число елементів сукупності з однаковими варіантами називають вагами.

Значення ознаки усереднюється за формулою середньої арифметичної зваженої:

= = ,

де хі – значення ознаки, fi – частота, di – частка.

Середня гармонійна проста: х=n/Σ1/х_і

Середня гармонійна зважена: х=Σf_і/Σfі/х_і

Середня геометрична проста:х=

Середня гармонійна зважена:

Властивості середньої арифметичної:

1)Сума відхилень окремих значень ознаки від середньої перемноженої на ваги=0 Σ(х_і-х)=Σх_і-nх= Σх_і-nΣх/n=0(арифмет проста) Σ(х_і-х)f= Σх_іf_і-хΣf_і= Σх_іf_і/Σf_і

2).Якщо всі значення варіант збільшити чи зменшити в ту саму к-сть разів,то середня збільшиться або зменшиться в стільки ж разів. Σ(х_ік) f_і/ Σf_і=к Σх_іf_і/Σf_і=кх Σх_і/кf_і/ Σf_і=1/к Σх_іf_і/Σf_і=х/к

3)якщо до усіх значень варіант «+»чи «-» ту саму постійну вел,то середня збільшиться або зменшиться ту ж саму вел: Σ(х_і-+а)f_і/Σf_і= Σх_іf_і/Σf_і-+Σаf_і/Σf_і=х-+ Σаf_і/Σf_і=х-+а

4)якщо ваги помножити або поділити на будь-яке постійне число,то середня не зміниться.х=Σх_і(f_іb)/Σf_іb=bΣх_іf_і/bΣf_і= Σх_іf_і/Σf_і=x

5)Добуток середньої на суму частот=сумі добутків варіант на частоти. x Σf_і= Σх_іf_і/Σf_і Σf_і= Σх_іf_і

6)Загальна середня=середній із часткових середніх зважених за чисельністю відповідних частин сукупності. X= x_іf_і+ X₂f₂+…+X_nf_n/f₁+f₂+f₃=Σx_іf_і/Σf_і

4.5. Система статистичних показників

Системи показників, що має дві особливості: 1) всебічність кількісного відображення явищ; 2) органічний взаємозв’язок окремих показників, причому саме вони перетворюють групу показників на єдиний комплекс характеристик складного явища чи процесу.

Коло властивостей, що вивчаються, а отже, і показників системи залежить від мети дослідження. У кожній системі можна вирізнити певні множини показників, які детальніше відтворюють той чи інший бік явища. Систему показників визначають як ієрархічну структуру, на нижньому щаблі якої — узагальнюючий інтегральний показник, на верхньому — рівновагомі ознаки, які безпосередньо вимірюються. 

Кожний показник системи має самостійне значення і водночас є складовою узагальнюючої властивості. априклад, при вивченні конкурентоcпроможності продукції в шинній промисловості безпосередньо вимірюються твердість, опір стиранню, модуль еластичності, міцність протектора, а також пробіг шин до ремонту. Ці ознаки визначають надійність і довговічність продукції, які, у свою чергу, є параметрами якості. Інші ознаки формують блок ефективності виробництва шин. Якість та ефективність визначають конкурентоспроможність продукції.