6.1.Моменти розподілу.

Момент розподілу – середнє значення к-х степенів відхилень варіантів від довільного постійного числа А. Загальний формалізований вигляд моменту розподілу:

Мк = , де Мк – момент к-ого порядку.

Розрізняють:

Початкові моменти (А=0) Мк =

Центральні моменти ( А= ) =

Умовні моменти ( А= хо) mk =

Момент нульового порядку розраховується для:

Початкового моменту Мо = = 1

Центрального = = 1

Умовного m1 =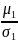 = 0/ = 0

Момент другого порядку( к=2) розраховується для:

Початкового моменту М2 = =

Центрального = =

Стандартизованого m2 = = = 1

Момент третього порядку (к=3) розраховується для:

Початкового моменту М3 =

Центрального =

Умовного m3 =

Взаємозв»язок між центральними і початковими моментами:

= М3 – 3М2М1+ 2

= М4 – 4М3М1+ 6М2

Властивості центральних моментів:

1.Із збільшенням або зменшенням усіх варіантів на одне і теж число А величина центрального моменту не зміниться.

2. Із збільшенням або зменшенням усіх варіант в А разів величина центрального моменту збільшиться або зменшиться в . Ці властивості використовуються, якщо необхідно створити новий ряд та ввести умовний нуль:

- де h – ширина інтервалу

- А – умовний нуль, за який беруть середину інтервалу з найбільшою частотою

Хо =

Перехід до центральних моментів вихідного емпіричного ряду здійснюється за формулою: μк = μк(0) . Моменти розподілу використовуються в оцінці асиметрії та ексцесу рядів розподілу.

6.2. Асиметрія

Асиметрія – характеризує скошеність ряду розподілу від центра праворуч або ліворуч.

Відносні показники симетрії обчислюються: Аs = As =

Якщо As - правостороння асиметрія, якщо Аs - лівостороння асиметрія

Для аналізу асиметрії ряду розподілу використовують стандартний момент третього порядку Аs = m3 = . Якщо Аs 0,25 – асиметрія є незначною, якщо Аs асиметрія є значною.

Середньоквадратична похибка асиметрії характеризує істотність коефіцієнту асиметрії

= , де н – обсяг сукупності. Якщо , то асиметрія розподілу значна , а розподіл ознаки у генеральній сукупності несиметричний.

6.3. Ексцес

Міра ексцесу – це крутизна розподілу залежно від варіації ознаки.

Ех = m4 – 3 = – 3. Якщо Ех 0 – гостро вершинний розподіл, якщо Ех = 0 - ексцес відсутній, якщо Ех 0 – плоско вершинний розподіл.

Середньоквадратична похибка ексцесу характеризує істотність міри ексцесу:

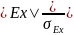
= . Якщо 3, то ексцес ряду розподілу властивий і генеральній сукупності.

11.3. Методи порівняння паралельних рядів даних.

Для вивчення стохастичних зв’язків використовується метод порівняння паралельних рядів 2-ох показників , 1-н з яких є факторним Х , а 2-гий - результативним У. При цьому основними завданнями застосування цього методу є оцінка тісноти взаємозв’язку та визначення його напрямку на основі розрах. Спец. Коефіцієнтів.

Найпростішим показником є коефіцієнт Фехнера ( Кф): Кф=С-Н/С+Н

С – число співпадінь знаків відхилень від середньої

Н – число неспівпадінь знаків відхилень від середньої

Якщо виконується нерівність Х≥Х (середнє) або У≥У ( середнє), значенню присвоюється знак «+», в протилежному випадку – знак «-». В тому випадку, коли по обох показниках знаки одинакові, має місце їх спів падіння, а коли вони різні – неспівпадіння. Коефіцієнт Фехнера знаходиться в межах від -1 до+1 . Якщо |Кф|→0, зв'язок між показниками слабкий , а при |Кф|→1 зв'язок тісний. Цей коефіцієнт має додатнє значення при наявності прямого зв’язку, а відємне – при оберненому.

Більш досконалим показником вважається коефіцієнт кореляції рангів Спірмена (р) :

Р= 1-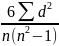 d= rx-ry – різниця рангів факторного та результативного показників.

При цьому під рангом розуміють порядковий номер значення показника у порядку зростання або зменшення. Коефіцієнт кореляції рангів також змінюється від -1 до +1. При р>0 зв'язок між показниками прямий , а при р<0- обернений. Якщо |р| наближається до 1 , між показниками існує тісний зв'язок , якщо |р|<0,3 вважається, що взаємозв’язок практично відсутній.