
- •1.Статистика як наука
- •2.Предмет, метод, завдання, осн. Поняття
- •3.Поняття про статистику.
- •4.Історія статистики як науки.
- •5.Основні риси предмету статистики та його значення
- •6. Теоретичні засади статистики як науки.
- •7. Особливості статистичної методології. Метод статистики
- •8. Загальна теорія статистики як галузь статистичної науки
- •9.Поняття про статистичне спостереження та етапи його проведення.
- •10. Основні організаційні форми, види та способи статистичного спостереження.
- •11. Програмно-методологічні питання статистичного спостереження.
- •12. Суть та завдання статистичного зведення.
- •14. Точність спостереження
- •13. Класифікація зведення:
- •14. Принципи формування груп.
- •15. Статистичні таблиці, їх види та правила побудови.
- •16. Середні величини, види середніх величин.
- •4.5. Система статистичних показників
- •4.6 Інтегральні оцінки суспільних явищ
- •4.1. Суть і види статистичних показників
- •4.2. Абсолютні величини
- •4.3. Відносні величини
- •5.2. Характеристики центру розподілу
- •5.3. Характеристики варіації.
- •5.4. Дисперсія: види та взаємозв»язок.
- •6.1.Моменти розподілу.
- •6.2. Асиметрія
- •6.3. Ексцес
- •11.3. Методи порівняння паралельних рядів даних.
- •11.4. Методи аналітичного групування.
- •11.5. Парний кореляційно - регресійний аналіз.
- •11.6. Множинна регресія і кореляція.
- •11.7. Оцінка тісноти взаємозв’язку між атрибутивними ознаками.
5.2. Характеристики центру розподілу
Центром тяжіння будь-якої статистичної сукупності є типовий рівень ознаки, узагальнююча характеристика усього різноманіття її індивідуальних значень. Такою характеристикою є середня величина( ).
За даними ряду розподілу середня обчислюється як арифметична зважена:
 =
=
 , де хі – значення ознаки, fi
– частота,
di
–
частка.
, де хі – значення ознаки, fi
– частота,
di
–
частка.
В інтервальних рядах як варіанту хі використовують середину інтервалу.
Мода( Мо) – найбільш поширене значення ознаки, тобто варіанта, яка має найбільшу частоту. Удискретних рядах моду визначають візуально за найбільшою частотою ( часткою). Існують бімодальні і полімодальні ряди розподілу. В інтервальному ряді розподілу мода визначається за формулою:
Мо
= хо + h ,
де
хо – нижня межа модального ряду, h
– крок(ширина)
модального інтервалу,
,
де
хо – нижня межа модального ряду, h
– крок(ширина)
модального інтервалу,
 - частоти перед модального, модального
і після модального.
- частоти перед модального, модального
і після модального.
Медіана (Ме) – варіанта, яка припадає на середину впорядкованого ряду і ділить його навпіл. У дискретному ряді медіаною буде значення ознаки, кумулятивна частота, якої перевищує половину обсягу сукупності, тобто
 >=
1|2
>=
1|2
 , для
частки
, для
частки
 ≥0,5
≥0,5
В інтервальному ряді за принципом накопичення частоти за даної умови визначають медіальний інтервал, а медіану обчислюють за формулою:
Ме
= хо + h
 , де хо – нижня межа медіанного інтервалу,
h
– крок(ширина)
медіанного інтервалу,
, де хо – нижня межа медіанного інтервалу,
h
– крок(ширина)
медіанного інтервалу,
 - кумулятивна частота перед медіанного
інтервалу,
- кумулятивна частота перед медіанного
інтервалу,
 - частота медіанного інтервалу.
- частота медіанного інтервалу.
5.3. Характеристики варіації.
В одних сукупностях значення ознак щільно групуються навколо центру розподілу, в інших – значно відхиляються. Чим менші ці відхилення, тим одно рідніша сукупність. Вимірювання ступеня коливання ознаки – невід»ємна складова аналізу закономірностей розподілу.
Для вимірювання та оцінювання варіації використовують:
Абсолютні характеристики:
1.розмах варіації: R= Xmax – Xmin
2. середнє лінійне відхилення:
-
для не згрупованих даних
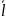 =
=
-
для
згрупованих даних
=
3. середнє квадратичне значення:
-
для не згрупованих σ=

- для згрупованих σ=
4. Дисперсія:
-
для не згрупованих
 =
=

- для згрупованих =
- Відносні характеристики варіації:
-
коефіцієнт асиміляції
 =
=
 . 100%
. 100%
-
лінійний коефіцієнт варіації
 =
=
 .100%
.100%
-
квадратичний коефіцієнт варіації
 =
=
 . 100%
. 100%
Якщо
 33%, то варіація не значна. Якщо
33%, то варіація не значна. Якщо
 33%, то варіація суттєва.
33%, то варіація суттєва.
5.4. Дисперсія: види та взаємозв»язок.
Ступінь варіації об»єкта характеризує показник середнього квадратичного відхилення( дисперсія) , що є середньою арифметичною із суми квадратів відхилень окремих варіант від їхньої середньої.
Формула дисперсії:Для не згрупованих = Для згрупованих =
Властивості дисперсії:
Дисперсія від постійної величини дорівнює 0
Якщо до кожної з варіант додати або відняти постійну величину, то дисперсія не зміниться
Якщо
кожну з варіант помножити або поділити
на постійну величину а, то дисперсія
збільшиться або зменшиться в
 разів
разів
Дисперсія відносно довільної величина а є більшою від дисперсії відносно середньої величини на квадрат різниці між середньою і цією постійною величиною
Види дисперсії:
Загальна дисперсія – характеризує загальну варіацію ознаки під впливом усіх умов і причин, що зумовили варіацію
Групова дисперсія – дорівнює середньому квадрату відхилень окремих значень ознаки всередині групи від середньої арифметичної відповідної групи. Вона відображає варіацію ознаки лише за рахунок умов, що діють в середині групи
Середня
з групових – це середня арифметична
зважена з групових дисперсій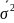 =
=

Міжгрупова
дисперсія характеризує варіацію
результативної ознаки за рахунок
групувальної ознаки.
 =
Правило
складання дисперсій:
=
+
Загальна
дисперсія може бути визначена як різниця
квадратів:
=
=
Правило
складання дисперсій:
=
+
Загальна
дисперсія може бути визначена як різниця
квадратів:
=
 –
–
 Варіація альтернативної ознаки:
=
pq=
p(1-p)Максимальне
значення альтернативної ознаки дорівнює
0,25.На основі загальної та між групової
дисперсії розраховують емпіричний
коефіцієнт детермінації, який набуває
значень від 0 до 1 та у відсотках показує
частку загальної варіації, що зумовлена
дією групування ознаки.
Варіація альтернативної ознаки:
=
pq=
p(1-p)Максимальне
значення альтернативної ознаки дорівнює
0,25.На основі загальної та між групової
дисперсії розраховують емпіричний
коефіцієнт детермінації, який набуває
значень від 0 до 1 та у відсотках показує
частку загальної варіації, що зумовлена
дією групування ознаки. =
=
 . Розраховують також емпіричне кореляційне
відношення, яке набуває значення від 0
до 1 та вказує на щільність зв»язку між
досліджуваними ознаками.
. Розраховують також емпіричне кореляційне
відношення, яке набуває значення від 0
до 1 та вказує на щільність зв»язку між
досліджуваними ознаками.
 =
=

