
- •Линейные операции над векторами.
- •Произведение а на скаляр.
- •Проекция вектора на ось.
- •Координаты вектора.
- •Векторное произведение векторов и его свойства.
- •Векторное произведение через координаты.
- •Полярное уравнение прямой.
- •Расстояние от точки до плоскости.
- •1) Угол между прямыми. Условия параллельности и перпендикулярности прямых.
- •X1ox2 – старая система координат, X`1o`X`2 - новая система координат, с ортами e`1 и e`2
Расстояние от точки до плоскости.
Пусть задана точка М0(х0;у0;z0) и плоскость Q со своим уравнением Ax+By+Cz+D=0
Расстояние d от точки М0 до плоскости Q находится по формуле:
![]()
Вывод этой формулы такой же, как вывод формулы расстояния от точки М0 до прямой линии.
Расстояние d от точки М0 до плоскости Q равно модулю проекции вектора М1М0, где М1(х1;у1;z1) – произвольная точка в плоскости Q на направлении нормального вектора n(A;B;C)










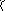 z
z
M0 n
 Q
Q
 0
M1
0
M1
y
 x
x
![]()
Так как точка М1(х1;у1;z1) принадлежит плоскости Q, то Ax1 + By1 + Cz1 + D =0, то есть
D = -Ax1 – By1 – Cz1
![]()
Отметим что если плоскость Q задана уравнением xcosα + ycosβ + zcosγ – p = 0, то расстояние от точки М0 до плоскости Q может быть найдено по формуле:
d =│x0cosα + y0cosβ + z0cosγ – p│
Уравнение прямой в пространстве.
Векторное уравнение прямой.
Положение прямой в пространстве вполне определено, если задать какую-либо точку М0 на прямой и вектор S параллельный этой прямой. Вектор S называется направляющим вектором прямой. Прямая линия L задана её точкой М0(х0;у0;z0) и направляющим вектором S(m;n;p). Возьмем на прямйо L произвольную точку М(х;у;z), обозначим радиус-векторы точек М0 и М, соответственно через r0 и r. Очевидно, что вектора r0, r и М0М связаны соотношением:
r = r0 + М0М (8)




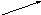
z
M1 S
M2
r
r0
 y
y
x
Вектор М0М, лежащий на прямой L параллельно направляющему вектору S, поэтому
М0М = tS, где t – скалярный множитель, называемый параметром, может принимать различные значения, в зависимости от положения точки М на прямой. Уравнение (8) можно записать в виде:
r = r0 + tS (9)
Полученное уравнение называется векторным уравнением прямой.
Замечая что r = (x;y;z); r0 = (x0;y0;z0); tS = (tm; tn; tp) уравнение (9) можно записать в виде:
xi + yj + zk = (x0 + tm)i + (y0 + tn)j + (z0 + tp)k. Следовательно следует равенство:
х = x0 + tm
y = y0 + tn (10)
z = z0 + tp
Уравнение (10) называется параметрическим уравнением прямой в пространстве.
Канонические уравнения прямой.
Пусть S = (m;n;p) – направляющий вектор прямой L и точка М0(х0;у0;z0) – точка лежащая на этой прямой. Вектор М0М, соединяющий точку М0 с произвольной точкой М прямой L, параллелен вектору S. Поэтому координаты вектора М0М(х-х0;y-y0;z-z0) и вектора S(m;n;p) – пропорциональны.
![]() (11)
(11)
Уравнение (11) называется каноническим уравнением прямой в пространстве.
Замечания:
1) Уравнение (11) можно было бы получить сразу из параметрических уравнений прямой (10)
2) Обращение в 0 одного из знаменателай уравнения (11) означает обращение в 0 соответственного числителя
Пример:
![]() - задает прямую, проходящую через точку
М0(2;-4;1) перпендикулярно оси Oz
(проекция вектора S на Oz
равна 0, но это означает что прямая лежит
в плоскости z=1 и поэтому
для всех точек прямая будет z-1=0)
- задает прямую, проходящую через точку
М0(2;-4;1) перпендикулярно оси Oz
(проекция вектора S на Oz
равна 0, но это означает что прямая лежит
в плоскости z=1 и поэтому
для всех точек прямая будет z-1=0)
Уравнение прямой, проходящей через две точки,
в пространстве,
В качестве вектора S можно взять вектор М1М2(х2-х1;y2-y1;z2-z1), то есть S= М1М2




 z
z
L
M1 M2
0 y
x
m = x2-x1; n = y2-y1; p = z2-z1
Поскольку прямая проходит через точку М1(х1;у1;z1), то согласно уравнению (11):
![]() (12)
(12)
Уравнение (12) называется уравнением прямой, проходящей через 2 точки.
Общие уравнения.
Прямую в пространстве можно задать, как линию пересечения двух непараллельных плоскостей. Рассмотрим систему уравнений:
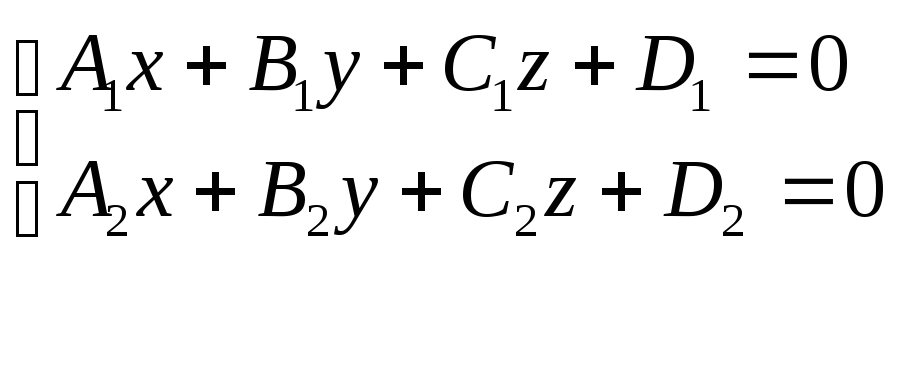

 (13)
(13)







Q1 Q2
S=n1×n2
n1 n2
n1 = (A1;B1;C1)
n2 = (A2;B2;C2)
Каждое из уравнений этой системы определяет плоскость. Если плоскости непараллельны (координаты векторов n1 и n2 непропорциональны), то система (13) определяет прямую L, как геометрическое место точек пространства, координаты которых удовлетворяют каждому из уравнений системы. Уравнения (13) называют общими уравнениями прямой.
От общих уравнений прямой (13) можно перейти к каноническим уравнениям (11). Координаты точки М0 на прямой L получаем из системы (13), придав одной из координат произвольное значение (например: z=0). Так как прямая L перпендикулярна векторам n1 и n2, то за направление S прямой L можно принять векторное произведение n1 и n2:
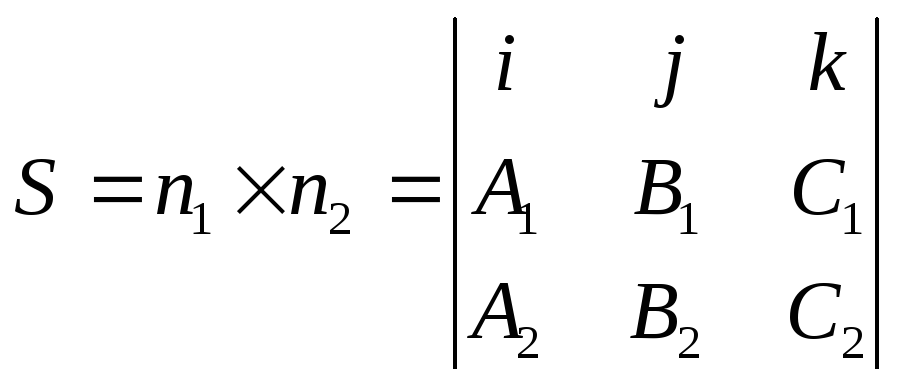
Замечания:
каноническое уравнение прямой легко получить, взяв две какие-либо точки на ней и применив уравнение (12)
Пример: написать каноническое уравнение прямой
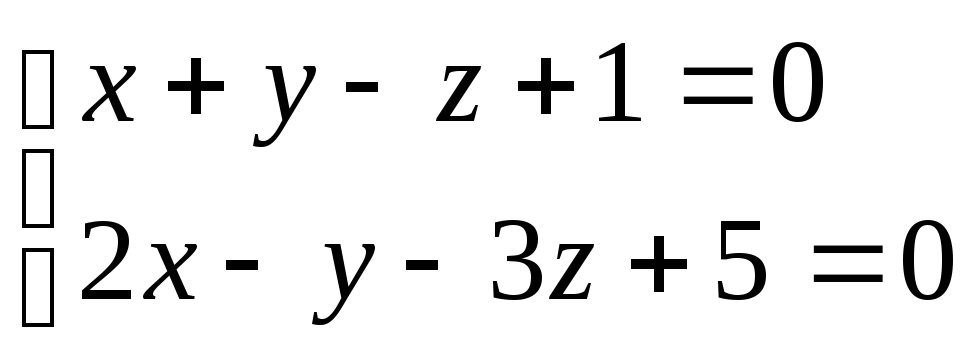
Решение:
Положим что z=0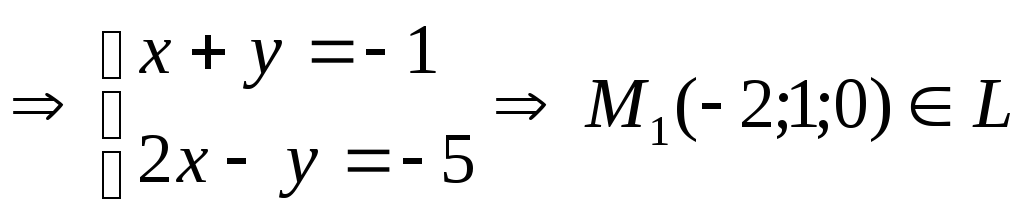
Положим что у=0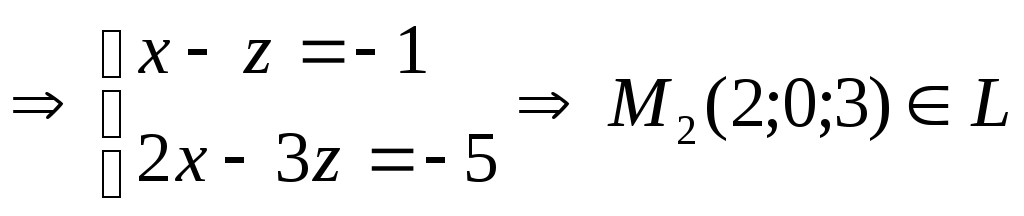
Записываем уравнение прямой L, проходящей через точки М1 и М2
![]()
Прямая линия в пространстве.
Основные задачи.
