48

Понятия об определителях и их основные свойствах.

Определители 2-го порядка

Пусть дана квадратная таблица из следующих чисел:

(1)

Число а₁₁∙а₂₂ – а₁₂∙а₂₁ называется определителем 2-го порядка и соответствует таблице (1). Этот определитель обозначается символом:

Числа а₁₁,а₂₂ , а₁₂,а₂₁ элементами определителя. Говорят, что элементы а₁₁,а₂₂ лежат на главной диагонали определителя, а а₁₂,а₂₁ - на побочной.

Таким образом определитель 2-го порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях.

Определители 3-го порядка.

Рассмотрим таблицу из 9-ти элементов:

(2)

Определителем 3-го порядка, соответствующий таблице (2), называется число, равное:

а₁₁∙а₂₂∙а₃₃ + а₂₁∙а₂₃∙а₃₁ + а₂₁∙а₃₂∙а₁₃ - а₁₃∙а₂₂∙а₃₁ - а₁₁∙а₃₂∙а₂₃ - а₂₁∙а₁₂∙а₃₃

Этот определитель обозначается символом:

При вычислении определителя 3-го порядка удобно пользоваться правилом треугольника (правилом Саррюса):

+

- первое действие

- второе действие

Свойства определителей:

1. Равноправность строк и столбцов: определитель не изменится, если его строки заменить столбцами или наоборот

2)При перестановке двух параллельных рядов, определитель меняет знак.

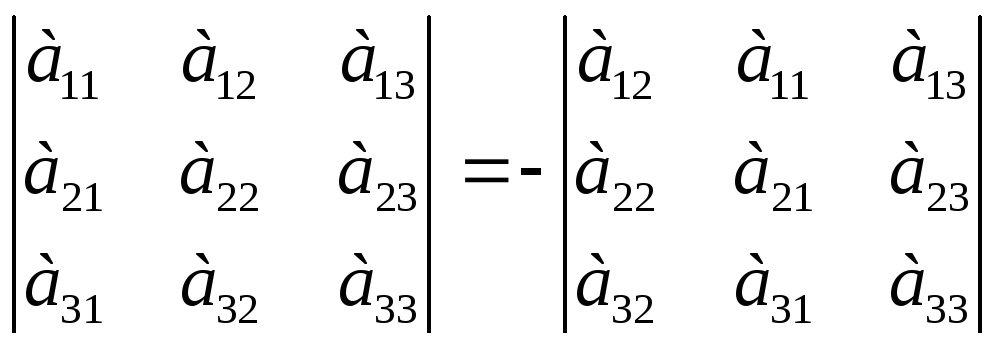
3)Определитель, имеющий два одинаковых ряда, равен 0

4)Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен 0

5) Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

6)Элементарные преобразования определителя.

Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

Пример: доказать что

Доказательство:

0 (cв-ва 4 и 3)

Минором некоторого элемента а_ij определителя n-ого порядка называется определитель n-1 –ого порядка, полученный из исходного, путем вычеркивания i – строки, j – столбца

Обозначается М_ij

Алгебраическим дополнением элемента А_ij определителя называется его минор (М_ij), взятый со знаком «+», если сумма i+j – четное число, «-» если i+j – нечетное число.

А = (-1)^i+j∙M_ij

7)Разложение определителя по элементам некоторого ряда.

Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения:

= а₁₁А₁₁+а₁₂А₁₂+а₁₃А₁₃

=а₁₁(а₂₂а₃₃ – а₂₃а₃₂) – а₁₂(а₂₁а₃₃ – а₃₁а₂₃) + а₁₃(а₂₁а₃₂ – а₃₁а₂₂) = а₁₁а₂₂а₃₃ – а₁₁а₂₃а₃₂ – а₁₂а₂₁а₃₃ +

+ а₁₂а₃₁а₂₃ + а₁₃а₂₁а₃₂ – а₁₃а₃₁а₂₂

8) Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна 0.

= а₁₂А₁₁+а₂₂А₁₂+а₂₃А₁₃ = 0

Матрица.

Основные понятия.

Матрицей называется прямоугольная таблица чисел, содержащая m – строк одинаковой длинны, и n – столбцов одинаковой длины.

А_ij = (a_ij)

Матрицы равны между собой , если равны все соответствующие элементы этих матриц.

(А)=(В)

а_ij=b_ij

Матрицы, размером m×n называют матрицей n –ого порядка.

Квадратной матрицей, у которой все элементы, кроме элементов главной диагонали равны 0, называется диагональной.

Матрица, содержащая один столбец или одну строку называется вектор-столбцом или вектор-строкой соответственно.

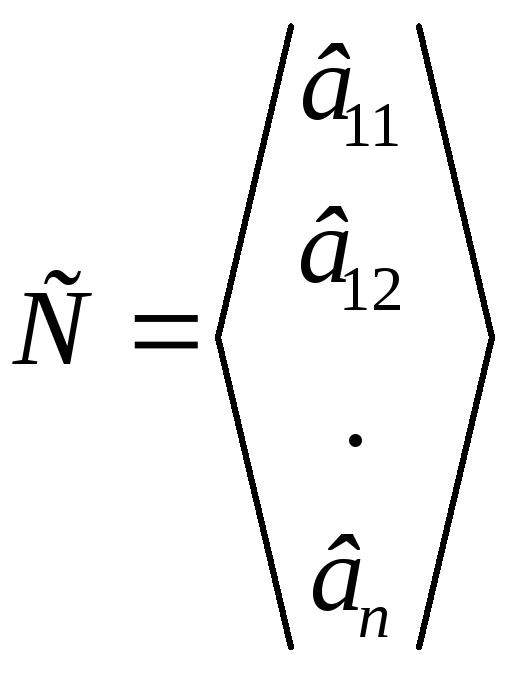- вектор – столбец

Матрица, полученная из данной матрицы, заменой каждой ее строки столбцом, с тем же номером, называется транспонированной и обозначается А^т

Пример:

Транспонированная матрица обладает следующим свойством: (А^Т)^Т=А

Действия над матрицами.

1)Сложение.

Операция сложения матриц вводится только для матриц одинаковых размеров.

А_m×n=(a_ij) B_m×n=(b_ij) А_m×n+ B_m×n= C_m×n

Где C_m×n = (a_ij) + (b_ij) = (a_ij + b_ij)

Пример:

2. Разность. Определяется аналогично сумме.

3)Умножение на число.

К× А_m×n= К(a_ij) = (Кa_ij)

Операции сложения матриц и умножения на число обладают следующими свойствами:

1. А + В = В + А

2. A + В + С = (А + В) + С

3. А + (-А) = 0

4. А + 0 = А

5. 

6)

7)

Элементарные преобразования матриц.

Элементарными преобразованиями матриц являются:

1)перестановка местами двух параллельных рядов

2)умножение всех элементов ряда матрицы на число, отличное от 0

3)прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число

Две матрицы А и В называются эквивалентными, если одна из них получается из другой, с помощью элементарных преобразований.

А~В – записывается

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны 0. Такую матрицу называют канонической.

Пример:

Произведение матриц.

Операция умножения 2 –х матриц вводится только для случая, когда число столбцов одной матрицы равно числу строк второй матрицы.

Произведением матриц А_m×n=(a_ij) и B_m×n=(b_ik) называется такая матрица С_m×n=(С_ik), такая что:

С_ik = a_i1b_1k + a_i2b_2k + a_i3b_3k + …..+a_inb_nk i = 1→m k = 1→ p

,то есть элементы i -той строки и к –ого столбца матрицы произведения С равны сумме произведений элементов i –той строки матрицы А на соответствующий элемент К –ого столбца матрицы В.

Матрицы А и В называются перестановочными, если А×В = В×А

Умножение матриц обладает следующими свойствами:

1)А×(В×С) = (А×В)×С

2)А×(В+С) = АВ + АС

3)(А+В)×С = АС + ВС

4)

Для операции транспонирования следующие свойства:

1)(А + В)^Т = А^Т + В^Т

2)(АВ) = В^ТА^Т

Невырожденные матрицы.

Основные понятия.

Пусть дана квадратная матрица n –ого порядка:

Квадратная матрица А называется невырожденной, если определитель ∆ = det А ≠ 0

В противном случае ∆ = 0 – матрица называется вырожденной.

Матрица союзная к матрице А, называется матрица:

,где А_{ij –} алгебраические дополнения

Матрица А^-1 называется обратной матрице А, если А∙А^-1 = А^-1∙А = Е, где Е – единичная матрица такого же порядка

Теорема.

Всякая невырожденная матрица имеет обратную. Приведем доказательство для 3 –ого порядка:

det A ≠ 0

Найдем А×А^*:

Итак получим: А∙А^* = detA∙Е

Аналогично убеждаемся что: А^*∙А= detA∙Е

Отсюда находим Е:

Сравнивая полученные результаты, получим:

, то есть

Отметим свойства обратной матрицы:

1. det(A^-1)=1/detA

2. (AB) = B^-1A^-1

3. (A^-1)^T = (A^T)^-1

Пример:

Дано: Наити: А^-1=?

А₁₁=1 А₂₁=-3 А₁₂=1 А₂₂=2

Ранг матрицы.

Рассмотрим матрицу А, размером m×n:

Выделим в ней К строк и К столбцов, где К ≤ min(n;m). Из элементов стоящих на пересечении выделенных строк и столбцов составим определитель К –ого порядка. Все такие определители называются минорами этой матрицы. В матрице А пунктиром выделим этот минор. В данный момент – это минор 2 –го порядка. Заметим, что таких миноров можно составить . С – комбинация, где:

;

Пример:

миноров

Наивысший порядок миноров матрицы, отличительных от 0 называется рангом матрицы.

Минор, порядок которого определяет ранг матрицы, называется базисным. У матрицы может быть несколько базисных миноров. Ранг матрицы обозначают r(A), rang(A)

Основные свойства ранга матрицы:

1. при транспонировании матрицы, её ранг не меняется

2. если вычеркнуть из матрицы нулевой ряд, то её ранг не изменится

3. ранг матрицы не изменится при элементарных преобразованиях матрицы

Ранг канонической матрицы равен числу единиц на главной диагонали. На этом основан один из способов вычисления ранга матрицы.

Пример:

- ранг этой матрицы равен 3, rangA = 3

Системы линейных уравнений.

Основные понятия.

а)Системой линейных алгебраических уравнений, содержащих m уравнений и n неизвестных, называется система вида:

(1)

, где а_ij – называется коэффициентом системы, а b_ij – свободным коэффициентом (свободным членом)

Такую систему можно записать в компактной матричной форме: Ах = В, где

Расширенной матрицей системы называется матрица Ă, дополненной свободными членами:

Решением системы называется n значений неизвестных (х₁ = l_1, x₂ =l₂…x_n=l_n), при подстановке которых все уравнения системы обращаются в верные равенства. Всякое решение системы можно записать в виде матрицы.

Система уравнений называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение и неопределенной, если имеет более одного решения. В последнем случае каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением. Решить систему, значит выяснить, совместна она или нет, если совместна, то найти её решения.

Две системы называются эквивалентными или равносильными, если они имеют одно и тоже общее решение. Другими словами, системы эквивалентны, если каждое решение одной из них является решением другой и наоборот. Эквивалентные системы получаются, в частности, при элементарных преобразованиях систем, при условии что преобразования выполняются лишь над строками матрицы.

Система линейных уравнений называется однородной, если все свободные члены равны 0:

Однородная система всегда совместна, то есть имеет решение, так как х₁ = х₂ = х_n= 0

Теорема Кронекера-Капели.

Система линейных алгебраических уравнений (1) совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу основной матрицы.

Выводы из теоремы:

1)если ранг совместной системы равен числу неизвестных, то система имеет единственное решение

2)если ранг совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений

3)ранг основной матрицы не может быть больше ранга расширенной матрицы

Решение невырожденных линейных систем.

Формула Крамера

Пусть дана система m линейных уравнений с n неизвестных. (система (1))

Эту систему удобно записать в матричной форме: Ах = В , где

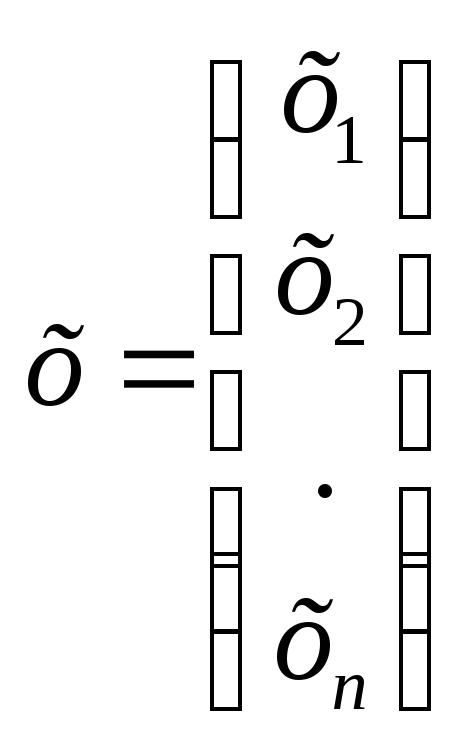
Определителем этой матрицы называется:

∆=detA

Если определитель системы отличен от 0 (∆≠0), то система называется невырожденной.

Найдем решение данной системы уравнений, в случае ∆≠0.

Умножим обе части уравнения Ах = В на А^-1 →А^-1Ах = А^-1В → Ех = А^-1В → х = А^-1В (2)

Отыскание решения системы по формуле (2) называют матричным способом решения системы.

Матричное равенство (2) запишем в виде:

=

А₁₁b₁+A₂₁b₂+…+A_n1b_n – есть разложение следующего определителя по алгебраическим дополнениям:

Определитель ∆₁ получается от определителя ∆, путем замены 1 –ого столбца коэффициентом-столбцом из свободных членов. Итак:

; ;

i = 1,n - формула Крамера

Векторная алгебра.

Вектора. Основные понятия.

При изучении различных разделов физики, механики и технических наук встречаются величины, которые полностью определяются заданием их числовых значений. Такие величины называются скалярными. Примерами скалярных величин являются длина, площадь, объем, масса, температура и другие. Помимо скалярных величин в различных задачах встречаются величины для определения которых кроме числового значения необходимо знать также их направление. Такие величины называются векторными. Примерами векторных величин могут служить сила, скорость и другие.

Вектором называется направленный отрезок, имеющий определенную длину, у которого одна из ограничивающих его точек принимается за начало, а вторая за конец. Если А – начало вектора и В – его конец, то вектор обозначается символом АВ. Вектор можно обоз-

начить и одной малой латинской буквой с черточкой над ней.

Начало вектора называют точкой его приложения. Если точка А является началом вектора а, то мы будем говорить, что вектор а приложен в точке а. Вектор ВА называется противоположным вектору АВ. Вектор, противоположный вектору а, обозначается –а. Длиной или модулем вектора АВ называется длина отрезка и обозначается │АВ│. Вектор, длина которого равна 0, то есть начало и конец его совпадают называется нулевым вектором и обозначается 0. Нулевой вектор направления не имеет. Вектор, длина которого равна 1, называется единичным вектором и обозначается через е. Единичный вектор, направление которого совпадает с направлением вектора а, называется ортом вектора а. Вектора а и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Коллинеарные вектора могут быть направлены одинаков, либо в противоположные стороны. Нулевой вектор считается коллинеарным любому вектору. Два вектора а и b называются равными, если они коллинеарные ,имеют одинаковые длины и имеют одно направление. Все нулевые вектора считаются равными. Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства, в частности плоскости. Такой вектор называется свободным.

Пример: В b С │AB│=│DC│

1 │AD│= - │BC│

a c

d

А D

Три вектора в пространстве называют комплонарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любых коллинеарны, то такие вектора компланарны.

α

а b

c

Линейные операции над векторами.

Под линейными операциями над векторами понимают операции сложения, вычитания векторов, а так же умножение вектора на число.

Пусть а и b произвольные вектора, возьмем произвольную точку 0 и построим вектор ОА= а и ОВ = b

A

а

a+b

b

O B

В таком случае сумма векторов производится по правилу параллелограмма.

Если начало и конец векторов соответствуют, то сумма векторов производится по правилу треугольника.

b

а a+b

a₂

a₁

a₃

a_n-1

a₁+..+a_n

a_n

Под разностью векторов а и b понимается вектор с, такой что b + c = a

a a – b = a + (-b)

a

c

b

Отметим, что в параллелограмме, построенном на векторах а и b, одна направленная диагональ является суммой векторов а и b, а другая разностью векторов. Можно вычитать векторы по правилу: а – b = a + (-b), то есть вычитание векторов заменить сложением вектора а с вектором противоположным вектору b.

Произведение а на скаляр.

Произведением вектора а на скаляр, называется вектор λа, который имеет длину │λ│∙│а│, коллинеарен вектору Q, имеет направление вектору а, если λ › 0 и противоположен по направлению, если λ ‹ 0.

Пример:

а b

2a -3b

Из определения произведения векторов на число следуют свойства этого произведения:

1. если b = λa , то b параллелен а

если а параллелен b и а ≠ 0, то при некотором λ, верно равенство λb = a

2) всегда а = │а│∙ а^-0 ,где а^-0 - орта вектора а .

то есть каждый вектор равен произведению его модуля на орт.

Линейные операции над векторами обладают следующими свойствами:

1. а + b = b + a

2) (a + b) + c = a + (b + c)

3) λ₁(λ₂a) = λ₁λ₂a

4) (λ₁+ λ₂)a = λ₁a + λ₂a

5) λ(a + b) = λa + λa

Эти свойства позволяют проводить преобразования в линейных операциях с вектором, как это делается в обычном алгебре: слагаемые меняют местами, вводят скобки, группируют, выносят за скобки, как скалярные, так и векторные общие множители.