Координаты вектора.
Найдем координаты вектора а = АВ, если известны координаты точек А(x1, y1, z1) и В(x2, y2, z2).
Z A Имеем : АВ = ОВ – ОА =(x2i+y2j+z2k)-(x1i+y1j+z1k)=
(x2- x1)i + (y2 - y1)j + (z2 - z2)k
B Следовательно, координаты вектора равны разнос-
ти соответствующих координат конца и начала век-
тора.
АВ = (x2- x1; y2 - y1; z2 - z2)
k
i j y
x
Скалярное произведение векторов и его свойства.
Скалярным произведением двух ненулевых векторов а и b называется число, равное произведению длин этих векторов на косинус угла между ними.
(1)
где φ – угол между векторами а и b
Формуле (1) можно придать иной вид, так как │а│cosφ = прba и │b│cosφ = праb , то получим:
(2)
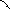
а
φ
b
То есть Скалярное произведение двух векторов равно модулю одного из них, умноженного на проекцию другого на ось.
Свойства скалярного произведения:
1) Скалярное произведение обладает переместительным свойством.
так как │а││b│= │b││a│, cos(a,b) = cos(b,a), то ab = ba
2)Скалярное произведение обладает сочетательным свойством, относительно скалярного множителя.
(λa)b = λ (ba)
(λa)b = │b│прbλa = λ│b│прba = λ (ab)
3) Скалярное произведение обладает распределительным свойством:
a(b + с) = ab + ac
a(b + c) = │a│пра(b+c) = │a│(прab+прac) = │a│прab+│a│прaс = ab + ac
4) Скалярный квадрат вектора равен квадрату его длины.
а2 = │а│2
а2 = а∙а = │а│∙│а│cos1 = │а│∙│а│= │a│2
В частности i2 = j2 = k2 = 1
Если а возвести скалярно в квадрат и затем извлечь корень, то получим не первоначаль-
ный вектор, а его модуль.
Пример:
Найти длину вектора с=3а-4b, если │а│=2;│b│=3; (a,b)=π\3
Решение:
│с│=
5)Если вектора a и b ненулевые, взаимно перпендикулярны, то их скалярное произведение равно 0.
Следовательно верно и обратное утверждение: если произведение векторов а и b равно 0, значит вектора взаимно перпендикулярны.
В частности: ij = jk = ki = 0
Выражение скалярного произведения через координаты.
Пусть заданы два вектора а = ахi + аyj + аzk и b = bхi + byj + bzk. Найдем скалярное произведение векторов, перемножая их, как многочлены и пользуясь таблицей скалярных произведений векторов i, j, k
|
|
i |
j |
k |
|
i |
1 |
0 |
0 |
|
J |
0 |
1 |
0 |
|
k |
0 |
0 |
1 |
a∙b = (ахi + аyj + аzk)( bхi + byj + bzk)= ахbх + аyby + аzbz
То есть a∙b = ахbх + аyby + аzbz
Пример: доказать что диагонали четырехугольника, заданного координатами вершин А(
-4;-4;4), В(-3;2;2), С(2;5;1) и D(3;-2;2), взаимно перпендикулярны.
Решение:
Составим вектора АС и ВD, лежащие на диагоналях данного четырехугольника, имеем:
АС(2-(-4);5-(-4);1-4)=(6;9;3) и BD(6;-4;0)
Найдем скалярное произведение этих векторов:
АС∙BD = 6∙6+9(-4)+0(-3) = 36-36 = 0
Следовательно вектор АС перпендикулярен вектору BD, значит диагонали четырехугольника ABCD взаимно перпендикулярны.
Угол между векторами.
Определение угла φ между векторами а (ах; аy; аz) и b(bх; by; bz)
Отсюда следует условие перпендикулярности ненулевых векторо a и b:
ахbх + аyby + аzbz = 0
Проекции вектора.
Нахождение проекции а на направление, заданное вектором b, может осуществляться по формуле:
или
, то есть
Работа постоянной силы.
(физический смысл)
Пусть математическая точка перемещается прямолинейно из положения А в положение В, под действием постоянной силы F, образующей угол φ с линией перемещения. АВ = S
Из физики известно, что A = FScos φ
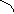
F
φ
A B
Таким образом работа постоянной силы при прямолинейном перемещении её точки приложения, равна скалярному произведению вектора силы на вектор перемещения.
Пример:
Вычислим работу, произведенную силой F=(3;2;4), если точка её приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7). Под каким углом к АВ направлена сила F?
Решение:
Находим S=AB=(4-2;2-4;7-6)=(2;-2;1)
A=FS=3∙2+2(-2)+4∙1=6 (ед. раб)
