Проекция вектора на ось.

Пусть в пространстве задана ось l α

M

M₁ L

Проекции точки М на ось l называется основание перпендикуляра ММ₁ опущенного из точки на ось. Точка М₁ – есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси. Если точка М лежит на оси l, то проекция точки М на ось совпадает с М.

Пусть АВ - произвольный вектор. │АВ│≠ 0. Обозначим через А₁ и В₁ проекции на ось l соответственно начало А и конец В вектора АВ и рассмотрим вектор А₁В₁

Проекции вектора АВ на ось l называется положительное число │А₁В₁│, если вектор А₁В₁ и ось l одинаковы направлены, и отрицательное число - │А₁В₁│, если вектор А₁В₁ и ось l противоположно направлены.

А В

А₁ В₁ l (и соотв

наоборот)

Если точки А₁ и В₁ совпадают (│А₁В₁│=0), то проекцией вектора АВ=0. Проекция вектора АВ на ось l обозначается: пр_lАВ. Если АВ = 0 или АВ перпендикулярен к оси l, то пр_lАВ=0.

Угол φ между вектором а и осью l изображен на рисунке:

A

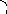φ l

Рассмотрим некоторые основные свойства проекции:

1) Проекция вектора а на ось l равна произведению модуля вектора а на cosφ

пр_l а= │а│∙ cosφ

Если

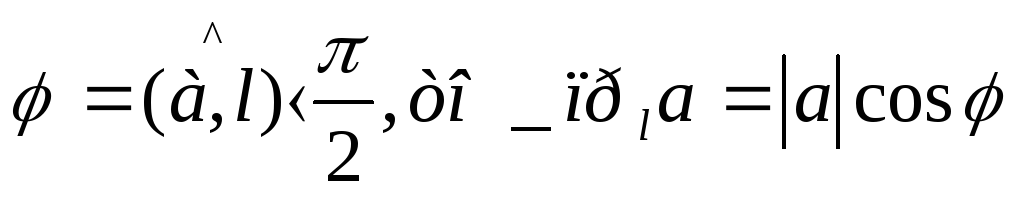
Если

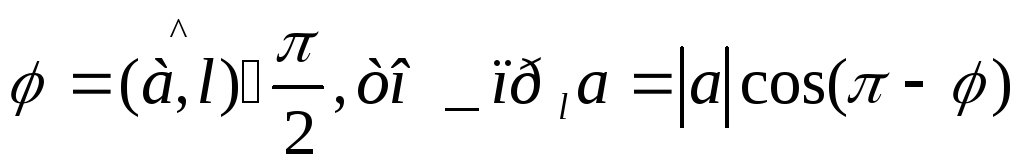
Если

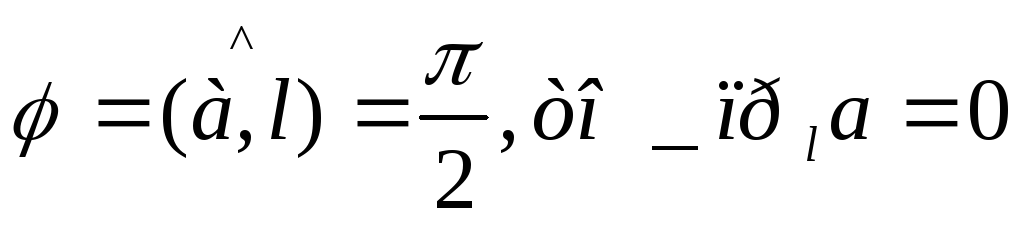
Следствие 1. Проекция вектора на ось положительна (отрицательна), если вектор образует острый (тупой) угол и равна 0, если этот угол прямой.

Следствие 2. Проекции равных векторов на одну и туже ось равны между собой.

2) Проекция суммы нескольких векторов на одну и туже ось равна сумме их проекций на эту ось. d = a + b + c ; пр_l(a+b+c) = пр_la + пр_lb + пр_lc

b

a с

d

a b l

d c

3) При умножении вектора а на число λ, его проекция на ось также умножается на это число: пр_l(λa) = λ пр_la

при λ›0 имеем: пр_l(λa) = │λa │cosφ = λ│a│ cosφ = λ пр_la

при λ‹0 имеем пр_l(λa) = │λa │cos(π-φ) = -λ│a│(-cosφ) = λаcosφ = λ пр_la

свойство спра ведливо при λ = 0

Разложение вектора по ортам координатных осей.

Модуль вектора. Направляющие косинусы.

Рассмотрим в пространстве прямоугольную систему координат OXYZ. Выделим на координатных осях ОХ, ОY и OZ единичный вектор (орт) И обозначим их i, j, k.

M₃

M

a

k

j M₂

i 0

M₁ N

Выберем произвольный вектор а и совместим его начало с начало координат а = │ОМ│. Найдем проекции вектора а на координатные оси. Проведем через конец вектора ОМ плоскости параллельно координатным плоскостям. Точки пересечения этих плоскостей с осями координат обозначим соответственно М₁, М₂, М₃., получим прямоугольный параллепипед , одной из диагоналей которого является вектор ОМ. Тогда: пр_ха = │ОМ₁│, пр_y│ОМ ₂│, пр_z│ОМ₃│. По определению суммы нескольких векторов находим: a = OM₁ + М₁N + NM. Т.к. М₁N = OM₂; NM = OM₃, то

а = OM₁ + OM₂ + OM₃ (1)

Но OM₁ = │OM₁│i; OM₂ = │OM₂│j; OM₃ = │OM₃│k (2)

Обозначи м проекцию а = ОМ, на оси ОХ, ОY и ОZ, соответственно а_х, а_y и а_z, то есть OM₁ = а_х ; OM₂ = а_y ; OM₃ = а_z. Из равенства (1) и (2) получаем:

а = а_хi + а_yj + а_zk (3)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_y и а_z называются координатами вектора а, то есть координаты вектора - есть его проекции на соответствующие координатные оси.

Векторное равенство (3) часто записывают в символическом виде: а (а_х; а_y; а_z)_. Равенство b (b_х; b_y; b_z) означает что b = b_хi + b_yj + b_zk. Зная проекции вектора а, можно легко найти выражение для модуля вектора. На основании о длине диагонали прямоугольного парралелепипеда: │ОМ│² = │OM₁│² + │OM₂│² + │OM₃│². Отсюда имеем:

(4)

Пусть углы вектора а с осями ОХ, OY и OZ ,соответственно, равны α, β и γ. По свойству проекций вектора на ось имеем:

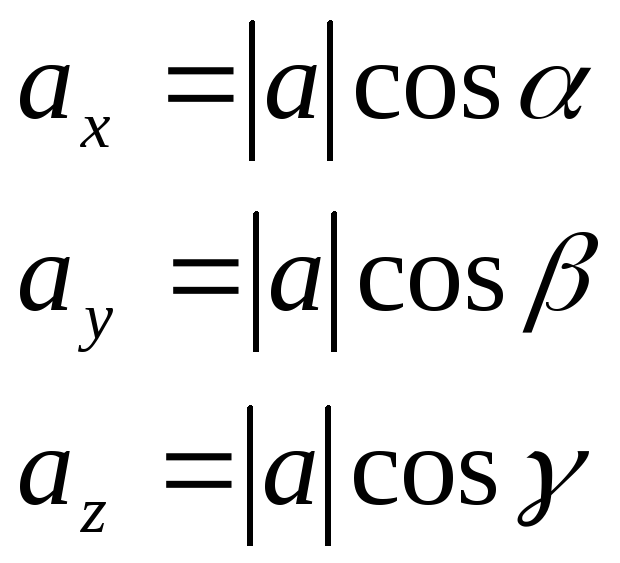
Следовательно:

(5)

Числа cosα, cosβ и cosγ называются направляющими косинусами вектора а. Подставим выражение (5) в равенство (4):

сosα² + cosβ² + cosγ² = 1

То есть сумма квадратов направляющих косинусов нулевого вектора равна 1. Легко заметить, что координатами единичного вектора е (cosα; cosβ; cosγ)

Итак, задав координаты вектора, всегда можно определить его модуль и направление (то есть сам вектор).

Действия над векторами, заданными проекциями.

Пусть векторы а = (а_х; а_y; а_z) и b = (b_х; b_y; b_z) заданы своими проекциями на оси координат OX, OY и OZ или что тоже самое:

а = а_хi + а_yj + а_zk

b = b_хi + b_yj + b_zk

Линейные операции над векторами.

Так как операции над векторами сводятся к соответствующим линейным операциям над проекциями этих векторов, то можно записать:

1)а ± b = (а_х ± b_х)i + (а_y + b_y )j + (а_z + b_z)k

а ± b = (а_х ± b_х; а_y ± b_y ; а_z ± b_z)

2)λa = λ а_хi +λ а_yj + λа_zk

λa = (λ а_хi; λ а_yj; λа_zk)

Равенство векторов.

Два вектора а и b равны тогда и только тогда, если

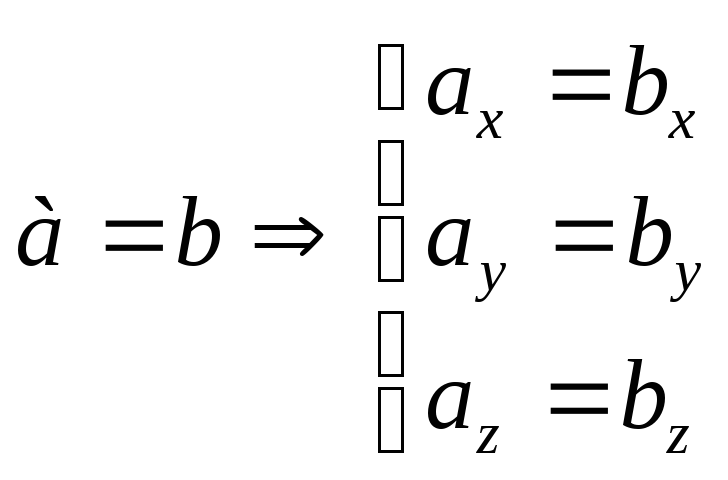
Коллинеарность векторов.

Выясним коллинеарность векторов а и b, заданными своими координатами. Так как а параллелен b, то можно записать а = λb, где λ = const., то есть:

а_хi + а_yj + а_zk = λ (b_хi + b_yj + b_zk) = λ b_хi + λ b_yj + λ b_zk, отсюда: а_х= λ b_х ; а_y = λ b_y; а_z= λ b_z ,

то есть:

Таким образом проекции коллинеарных векторов пропорциональны. Верно и обратное утверждение: вектора, имеющие пропорциональные координаты коллинеарны.

Координаты точки.

Пусть в пространстве задана прямоугольная декартова система координа Оxyz. Для любой точки М координаты вектора ОМ называются координатами точки М.

z

М

r

0. у

х

Вектор ОМ называется радиус-вектором точки М, и обозначается ОМ = r. Следовательно координаты точки – это координаты её радиус-вектора r(x, y, z) или r=xi + yj + zk. Координаты точки М записываются: М(x, y, z)