Методические рекомендации по построению сетевых моделей

При построении сетевого графика необходимо следовать следующим правилам:

     длина стрелки не зависит от времени выполнения работы;

     стрелка может не быть прямолинейным отрезком;

     для действительных работ используются сплошные, а для фиктивных – пунктирные стрелки;

     каждая операция должна быть представлена только одной стрелкой;

     между одними и теми же событиями не должно быть параллельных работ, т.е. работ с одинаковыми кодами;

     следует избегать пересечения стрелок;

     не должно быть стрелок, направленных справа налево;

     номер начального события должен быть меньше номера конечного события;

     не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме исходного;

     не должно быть тупиковых событий (т.е. не имеющих последующих событий), кроме завершающего;

     не должно быть циклов

Исходные данные для построения сетевой модели могут задаваться различными способами, например,

        описанием предполагаемого проекта. В этом случае необходимо самостоятельно разбить его на отдельные работы и установить их взаимные связи;

        списком работ проекта. В этом случае необходимо проанализировать содержание работ и установить существующие между ними связи;

        списком работ проекта с указанием их упорядочения. В этом случае необходимо только отобразить работы на сетевом графике.

Построение сетевого графика необходимо начинать с выявления исходных работ модели. Если согласно условию некоторая работа может выполняться, не ожидая окончания каких-либо других работ, то такая работа является исходной в сетевой модели и ее начальным событием является исходное событие. Если исходных работ несколько, то их стрелки выходят все из одного исходного события.

Если, согласно условию, после окончания некоторой работы не должны выполняться никакие другие работы, то такая работа является завершающей работой сетевой модели и ее конечным событием является завершающее событие. Если завершающих исходных работ несколько, то их стрелки заходят все в одно завершающее событие.

Если, согласно условию, несколько работ имеют общее начальное и общее конечное события, то они являются параллельными, имеют одинаковый код, что недопустимо. Для устранения параллельности работ вводят дополнительное событие и фиктивную работу (которой в реальности не соответствует никакое действие) таким образом, чтобы конечные события работ различались (рис.7.3.).

6. ЗАКОН РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

РАСПРЕДЕЛЕНИЕ ВЕРОЯТНОСТЕЙ (в математической статистике)— ряд чисел, показывающих, как часто встречается то или иное значение случайной величины, или соответствующая таблица, диаграмма или математическая формула, их заменяющая. Различают эмпирические Р. в., получаемые в результате экспериментов и измерений, и теоретические Р. в. (к которым бывает удобно с той или иной точностью приводить эмпирические Р. в.)

Закон распределениявероятностей дискретной случайной величины.

Определение: Случайной называется величина, которая в результате испытания принимает только одно значение из возможного множества своих значение, наперед неизвестное и зависящее от случайных причин.

Различают два вида случайных величин: дискретные и непрерывные.

Определение: Случайная величина Х называется дискретной (прерывной), если множество ее значений конечное или бесконечное, но счетное.

Другими словами, возможные значения дискретной случайной величину можно перенумеровать.

Описать случайную величину можно с помощью ее закона распределения.

Определение: Законом распределения дискретной случайной величины называют соответствие между возможными значениями случайной величины и их вероятностями.

Закон распределения дискретной случайной величины Х может быть задан в виде таблицы, в первой строке которой указаны в порядке возрастания все возможные значения случайной величины, а во второй строке соответствующие вероятности этих значений, т.е.

x	x1	x2	х3	…	хn
p	р1	р2	р3	...	рn

й

где р₁+ р₂+…+ р_n=1

Такая таблица называется рядом распределения дискретной случайной величины.

Если множество возможных значений случайной величины бесконечно, то ряд р₁+ р₂+…+ р_n+… сходится и его сумма равна 1.

Закон распределения дискретной случайной величины Х можно изобразить графически, для чего в прямоугольной системе координат строят ломаную, соединяющую последовательно точки с координатами (x_i;p_i), i=1,2,…n. Полученную линию называют многоугольником распределения (рис.1).

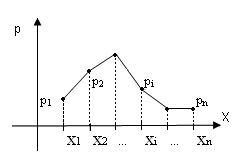
рис.1

Закон распределения дискретной случайной величины Х может быть также задан аналитически (в виде формулы):

P(X=x_i)=φ(x_i),i =1,2,3…n

7.Математическое ожидаение

Математическим ожиданием дискретной слу-

чайной величины называют сумму произведений всех ее

возможных значений на их вероятности.

Пусть случайная величина X может принимать только

значения xl, x2, ..., xn, вероятности которых соответ-

ственно равны р1, р2, . . ., pn. Тогда математическое ожи-

дание М (X) случайной величины X определяется равен-

ством

M(X)=x1p1+x2p2+…+xnpn или M(X)=∑xipi.

Свойства математического ожидания

Свойство 1. Математическое ожидание по-

стоянной величины равно самой постоянной:

М (С) = С.

Свойство 2. Постоянный множитель можно выно-

сить за знак математического ожидания:

М (СХ) = СМ (X).

Свойство 3. Математическое ожидание произведе-

ния двух независимых случайных величин равно произведе-

нию их математических ожиданий:

M(XY) = M(X)M(Y).

Свойство 4. Математическое ожидание суммы двух

случайных величин равно сумме математических ожиданий

слагаемых:

М (X + У) = М (X) + М (У).

8. Дисперсия

ДИСПЕРСИЯ ДИСКРЕТНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ [ dispersion, variance of a discrete random variable ]

     Дисперсией дискретной случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: D ( X ) = M ( X - M ( X )) ². Для вычислений удобнее пользоваться формулой :  D ( X ) = M ( X ² ) - ( M ( X )) ².       Дисперсия обладает следующими свойствами.         1. Дисперсия постоянной величины С равна нулю : D ( C ) = 0.         2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат : D ( CX ) = C ²D ( X ).         3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин:             D ( X+Y+Z ) = D ( X )+D ( Y )+D ( Z ).         4. Дисперсия суммы постоянной величины и случайной - равна дисперсии случайной величины: D ( C+X ) = D ( X ). 

ОСНОВЫ АЛГОРИТМИЗАЦИИ И ПРОГРАММИРОВАНИЯ