Вариант №7

1. Потенциальная энергия части имеет вид , где - модуль радиуса - вектора частицы, - постоянная величина. Найти силу действующую на частицу. Какую форму имеют поверхности, для которой модуль вектора силы постоянен? Изобразить эти поверхности для случаев

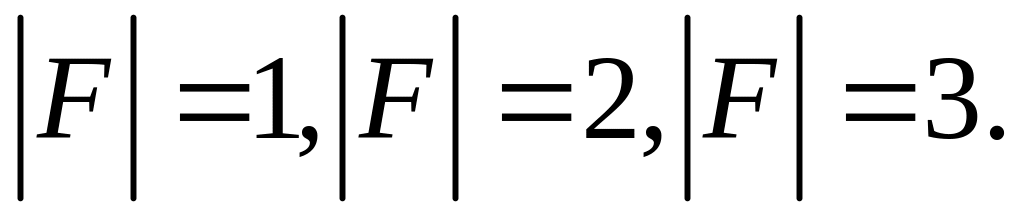
2. Найти производную скалярных полей в точке по направлению нормали к поверхности S: , образующей острый угол с положительным направлением оси Oz .

3. Показать, что поле вектора потенциально, найти потенциал поля.

4. Найти векторные линии поля вектора .

5. Вычислить циркуляцию вектора вдоль контура .

6. Вычислить поток поля через часть поверхности , лежащую в I октанте, в направлении внешней нормали.

7. Найти поток поля 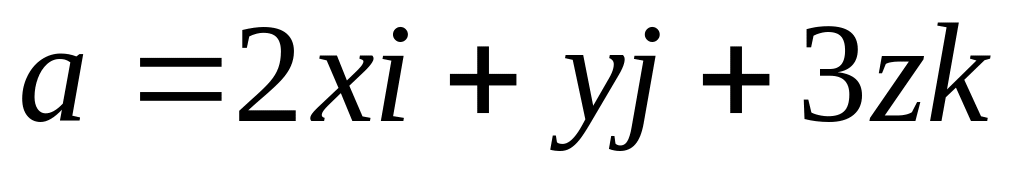через границу выпуклой области, заключенной между поверхностями и , в направлении внешней нормали.

8. Проверить формулу Стокса для поля вектора 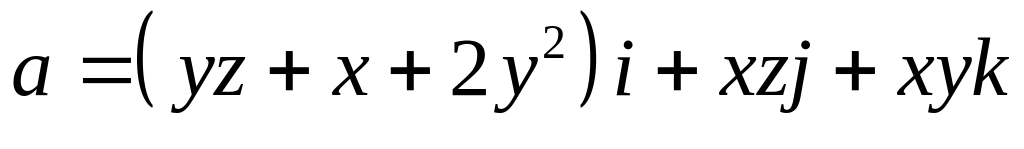, принимая за контур интегрирования окружность , а за поверхность интегрирования – поверхность цилиндра и .

9. Доказать, что если , - дважды дифференцируемые скалярные функции.

10. Найти и , для поля вектора , где

- радиус-вектор точки.

Вариант №8

1. Потенциал энергия частицы имеет вид Найти силу , действующую на частицу. Построить эквипотенциальные поверхности в случае u = 0, u = 1, u = 4.

2. Найти производную функции в точке в направлению градиента функции .

3. Показать, что поле вектора потенциально, найти потенциал поля.

4. Найти векторные линии поля вектора .

5. Вычислить работу вектора силы при перемещении по меньшей дуге кривой от точки к точке .

6. Вычислить поток поля через часть поверхности , лежащую в II октанте, в направлении внешней нормали.

7. Найти поток поля через часть поверхности , отсеченную плоскостью z = 2, в направлении внешней нормали.

8. Проверить формулу Стокса для поля вектора , принимая за контур интегрирования часть параболы и замыкающей её прямой z = 2, x = 0, а за поверхность интегрирования часть поверхности z = 2, ограниченную этим контуром.

9. Доказать, что 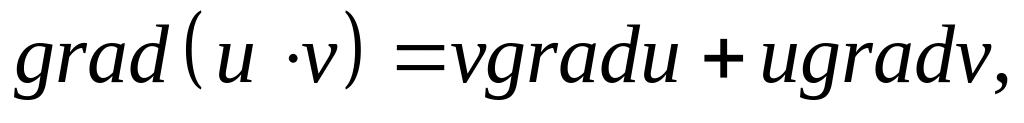где , - дифференцируемые функции. Проверить, что .

10. Для поля вектора найти потенциал, , и векторные линии, если - радиус-вектор точки.

Вариант №9

1. Потенциал энергия частицы имеет вид Найти силу , действующую на частицу. Какой вид имеют эквипотенциальные поверхности поля, в котором находится частица? Изобразить эти поверхности в случае

2. Найти производную скалярного поля в точке по направлению нормали к поверхности , образующей тупой угол с положительным направлением оси Oz .

3. Показать, что поле вектора потенциально, найти потенциал поля.

4. Найти векторные линии поля вектора .

5. Вычислить работу вектора силы при перемещении по кривой от точки к точке

6. Вычислить поток поля через плоский четырех с вершинами в точках М₁(1,-2,4), М₂(3,2,4), М₃(-1,2,4), М₄(-3,-2,4) в направлении оси Oz.

7. Найти поток поля через замкнутую поверхность, ограничивающую пространственную область 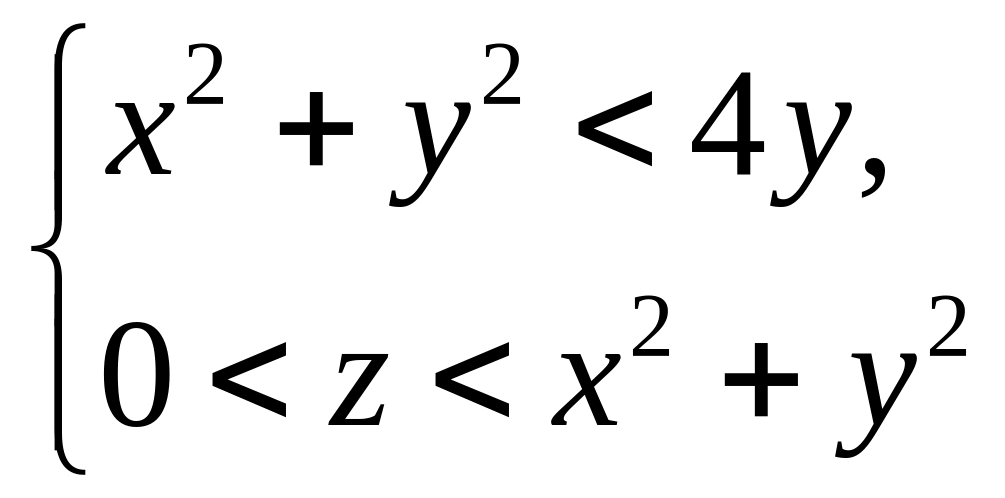, в направлении внешней нормали.

8. Проверить формулу Стокса для поля вектора , принимая за контур интегрирования окружность , а за поверхность интегрирования – любую поверхность, натянутую на эту окружность.

9. Доказать, что где - дифференцируемая функция.

10. Найти и для вектора где - радиус-вектор точки.