Расчетно-графическая работа «теория векторного поля»

Составители: преподаватели кафедры Вычислительных методов и уравнений математической физики.

Вариант №1

1. Найти производную поля в точке А(1,2,1) в направлении, образующем равные острые углы с осями координат.

2. Найти угол между градиентом скалярных полей и в точке .

3. Показать, что поле вектора 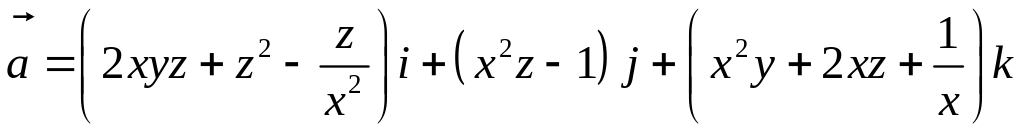потенциально, найти потенциал поля.

4. Найти векторные линии поля градиентов функции .

5. Вычислить работу силы при перемещении по линии из точки А(2,0,1) в точку В(0,4,1).

6. Вычислить поток поля через плоский треугольник с вершинами в точках А(2,0,0), B(0,-1,0), C(2,0,4). Нормальный вектор плоскости образует острый угол с осью Ох.

7. Найти поток поля через полусферу в направлении внешней нормали.

8. Проверить формулу Стокса для вектора , принимая за поверхность интегрирования боковую поверхность пирамиды, ограниченную плоскостями 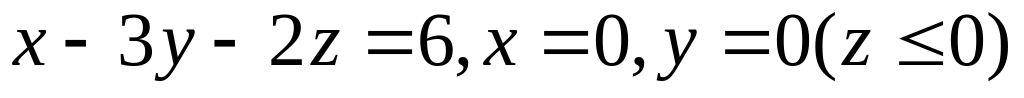, а за контур интегрирования – линию пересечения её с плоскостью z = 0.

9. Доказать, что .

10. Вычислить , где и постоянные векторы, а 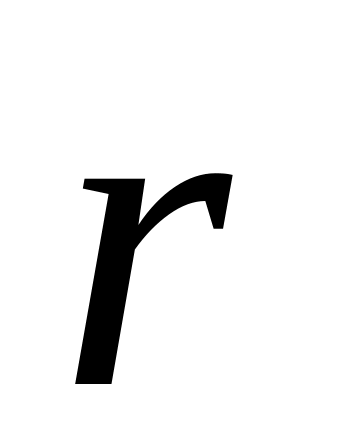- радиус-вектор точки.

Вариант №2

1. Дано скалярное поля 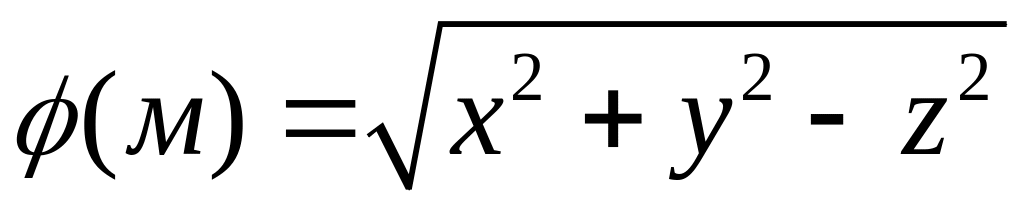. Найти Построить поверхность уровня для

2. Найти производную скалярных полей 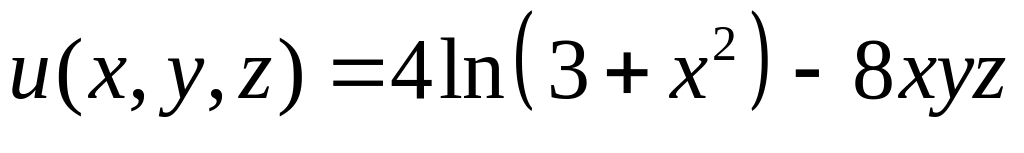в точке по направлению нормали к поверхности S: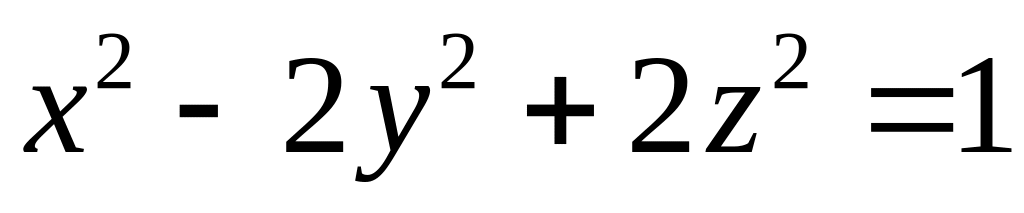 , образующей тупой угол с положительным направлением оси Oz .

3. Показать, что поле вектора потенциально, найти потенциал поля.

4. Найти векторные линии поля градиентов функции .

5. Вычислить работу силы при перемещении по линии (L): из точки в точку

6. Вычислить поток поля через часть поверхности , лежащую в I октанте и отсеченную плоскостями z = 0, z = 3, в направлении внешней нормали.

7. Найти поток поля через часть поверхности отсеченную плоскостями y = 3 в направлении внешней нормали.

8. Проверить формулу Стокса для поля вектора , принимая за поверхность интегрирования – поверхность, лежащей в I октанте образованную поверхностью и плоскостями x = 0, z = 0, а за контур интегрирования – линию пересечения этой поверхности с плоскостью

у = 0.

9. Доказать, что вектор ортогонален к , если - дифференцируемые скалярные функции.

10. Найти , где и , .

Вариант №3

1. Найти градиент поля , где , М(x,y,z). Построить поверхность уровня поля, соответствующие значениям

2. Найти производную скалярных полей в точке по направлению нормали к поверхности s: , образующей тупой угол с положительным направлением оси Oz .

3. Показать, что поле вектора потенциально, найти потенциал поля.

4. Найти векторные линии поля градиентов функции .

5. Вычислить работу силы при перемещении по линии от точки до точку

6. Вычислить поток поля 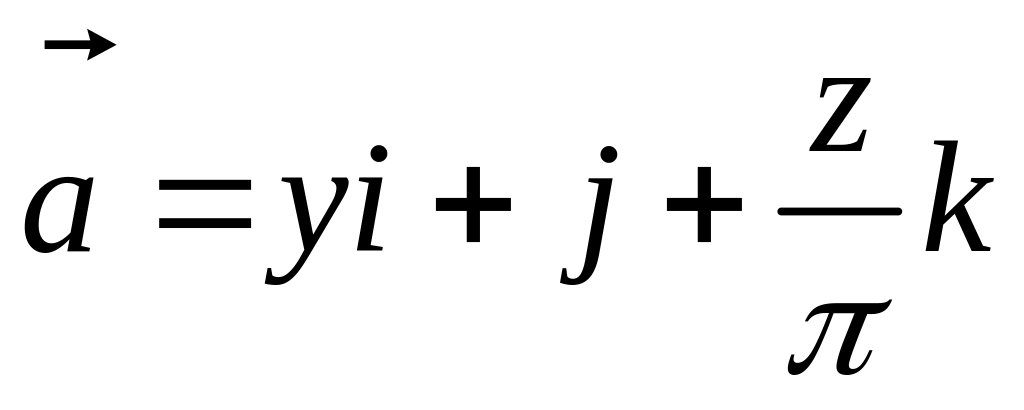через часть поверхности , лежащую в IV октанте, в направлении внешней нормали.

7. Найти поток поля 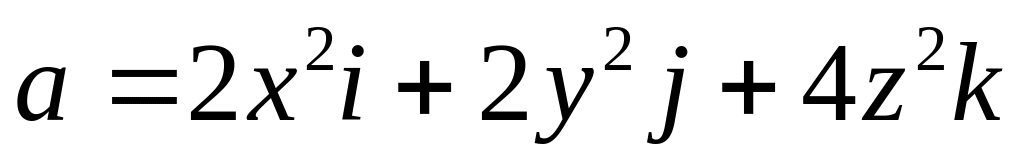через замкнутую поверхность, образованную полусферой и параболоидом , в направлении внешней нормали.

8. Проверить формулу Стокса для поля вектора , принимая за контур интегрирования окружность, а за поверхность интегрирования – поверхность цилиндра натянутую на этот контур.

9. Доказать, что вектор , где 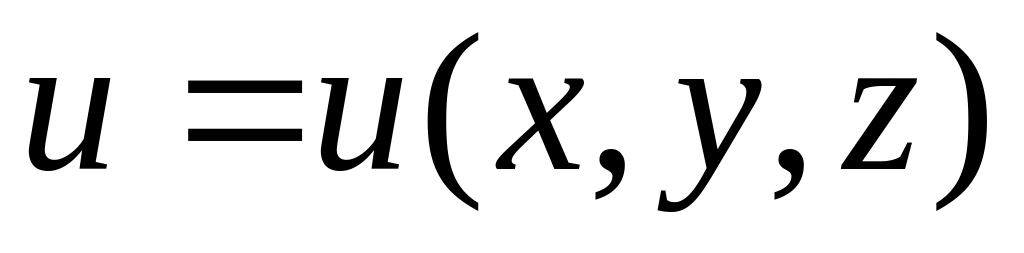- дифференцируемая функция.

10. Найти , где -радиус-вектор точки, - произвольная дважды дифференцируемая функция. В каком ?