
- •Определение булевой функции
- •Способы задания булевых функций
- •Формулы. Реализация функций формулами
- •Понятие суперпозиции
- •Эквивалентность формул. Основные тавтологии алгебры логики
- •Принцип двойственности
- •Разложение булевых функций по переменным. Совершенные
- •Полнота и замкнутость. Примеры функционально полных систем
- •Представление булевых функций полиномом Жегалкина
- •Класс функций, сохраняющий константу 0
- •Класс функций, сохраняющий константу 1
- •Класс самодвойственных функций
- •Класс линейных функций
- •Теорема Поста о полноте
- •Понятие днф. Проблема минимизации булевых функций
- •Геометрическая интерпретация задачи минимизации булевых функций
- •Определение тупиковой днф
- •Построение тупиковых днф методом упрощения совершенной днф
- •Определение сокращенной днф и геометрический метод ее построения
- •19.Минимизация булевых функций на основе построения тупиковых д. Н. Ф.
- •20. Минимизация булевых функций методом карт Карно.
- •21.Минимизация булевых функций методом Квайна-Мак-Класски
- •23.Задачи анализа и синтеза схем из функциональных элементов. Элементарные методы синтеза.
- •Элементарные методы синтеза
- •26 Синтез схем дешифратора и двоичного сумматора
- •28. Определение конечного автомата
- •Способы задания конечного автомата
- •29. Задача синтеза автоматов
- •Элементарные автоматы
- •Машина Тьюринга
- •Что собой представляет машина Тьюринга?
- •Пример работы машины Тьюринга
Понятие суперпозиции
Функцию , соответствующую формуле , будем называть суперпозицией функций из , а процесс получения функции из – операцией суперпозиции.
Операция суперпозиции включает две простые операции.
Операция подстановки переменных. Пусть
![]()
– подстановка
переменных, которая позволяет произвести
подстановку переменных у функции
и получить в результате функцию
![]() ,
где
,
где
![]() – любые переменные, не обязательно
различные. Очевидно, подстановка
переменных включает в себя переименование
переменных, перестановку переменных и
отождествление переменных. Обозначим
эту операцию буквой
– любые переменные, не обязательно
различные. Очевидно, подстановка
переменных включает в себя переименование
переменных, перестановку переменных и
отождествление переменных. Обозначим
эту операцию буквой
![]() :
:
![]() .
.
Операция бесповторной подстановки функций. Она позволяет строить выражения
 ,
где
– либо формула, либо переменная из
,
причем хотя бы одно из
отлично от переменной. Обозначим эту
операцию буквой
,
где
– либо формула, либо переменная из
,
причем хотя бы одно из
отлично от переменной. Обозначим эту
операцию буквой
 .
.
Таким образом, всякая формула над может быть получена из функций, принадлежащих , с помощью суперпозиции, то есть путем применения сначала операции бесповторной подстановки функций (многократной), а затем операции подстановки переменных (однократной).
Пример 3. Пусть имеется элемент, работа которого описывается некоторой булевой функцией (рис. 1,а). Результаты применения операции приведены на рис. 1,б (изменение обозначения входов) и рис. 1,в (подача одного и того же сигнала на несколько входов).





![]()
![]()


![]()
а) б) в)
Рис. 1. Иллюстрация применения операции
Пример 4. Выразим операцию отрицания через штрих Шеффера:
![]() ;
;![]() ;
;
![]() .
.
Пример
5.
Пусть
работа двух элементов
описывается
функциями
и
![]() .
Соединим элементы, как показано на рис.
2.
.
Соединим элементы, как показано на рис.
2.
f

![]()


g![]()

![]()
Рис. 2. Иллюстрация применения операции
Тогда
функция на выходе схемы получается в
результате подстановки функции
![]() на место третьего аргумента функции
:
на место третьего аргумента функции
:
![]() .
.
Пример
6. Рассмотрим
систему функций
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
.
Представим в виде суперпозиции этих функций сумму по модулю 2:
![]() ,
или
,
или
![]() .
.
Для стрелки Пирса по аналогии можно записать:
![]() ,
или
,
или
![]() .
.
4
Эквивалентность формул. Основные тавтологии алгебры логики
Ранее было показано, что каждой формуле над соответствует функция алгебры логики, причем различным формулам могут соответствовать равные функции.
Определение.
Формулы
и
называются эквивалентными,
если соответствующие им функции
![]() и
и
![]() равны, т. е.
равны, т. е.
![]() .
Запись
.
Запись
![]() означает, что формулы
и
эквивалентны.
означает, что формулы
и
эквивалентны.
Приведем список основных эквивалентностей (тождеств, тавтологий) алгебры логики, которые соответствуют теоретико-множественным тождествам, если заменить дизъюнкцию на объединение, конъюнкцию – на пересечение, отрицание – на дополнение.
 (коммутативность
дизъюнкции).
(коммутативность
дизъюнкции). (ассоциативность
дизъюнкции).
(ассоциативность
дизъюнкции).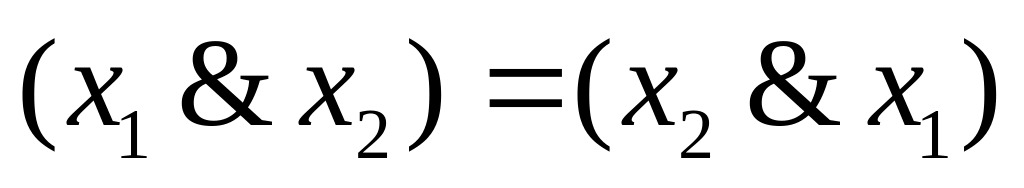 (коммутативность
конъюнкции).
(коммутативность
конъюнкции). (ассоциативность
конъюнкции).
(ассоциативность
конъюнкции). (правило
повторения для дизъюнкции).
(правило
повторения для дизъюнкции). (правило
повторения для конъюнкции).
(правило
повторения для конъюнкции).
 (операции
с 0 и 1 для дизъюнкции и конъюнкции).
(операции
с 0 и 1 для дизъюнкции и конъюнкции).
 (закон
двойного отрицания).
(закон
двойного отрицания).
 (правила
инверсии).
(правила
инверсии).
 (дистрибутивность
конъюнкции).
(дистрибутивность
конъюнкции). (дистрибутивность
дизъюнкции).
(дистрибутивность
дизъюнкции).
 (законы
де Моргана).
(законы
де Моргана).
18.
![]() .
.
19.
![]() .
.
Справедливость тождеств устанавливается сопоставлением таблиц истинности для функций, записанных в левых и правых частях тождеств.
С целью упрощения записи формул принимают следующие соглашения.
Приоритет логических связок. Пусть
 – множество логических связок:
– множество логических связок:
![]() .
.
а)
считают, что связка
![]() сильнее любой двухместной связки из
;
сильнее любой двухместной связки из
;
б)
связка
![]() считается сильнее, чем любая из оставшихся
связок.
считается сильнее, чем любая из оставшихся
связок.
2.
Обозначим через
![]() любую из связок
,
любую из связок
,
![]() .
В силу закона ассоциативности можно
вместо формул
.
В силу закона ассоциативности можно
вместо формул
![]() ,
,
![]() использовать выражение
использовать выражение
![]() ,
которое не является формулой, но может
быть превращено в нее путем расстановки
скобок.
,
которое не является формулой, но может
быть превращено в нее путем расстановки
скобок.
3. Внешние скобки у формул опускаются. Опускаются также скобки у выражения, над которым стоит знак отрицания.
Эти
соглашения позволяют, например, формулу
![]() записать в виде
записать в виде
![]() .
.
Рассмотрим некоторые следствия из тождеств 1 – 19.
Тождества 2 и 3 позволяют рассматривать логические суммы и произведения с любым числом слагаемых и результат не зависит от расстановки скобок. Поэтому далее будем использовать следующие обозначения:
![]() ,
,
![]() .
.
Удобно сформулировать ряд правил, вытекающих из тавтологий.
Если в логическом произведении один из сомножителей равен 0, то и произведение равно 0.
Если в логическом произведении, содержащем не менее двух сомножителей, имеется сомножитель, равный 1, то этот сомножитель можно зачеркнуть.
Если в логической сумме, содержащей не менее двух слагаемых, имеется слагаемое, равное 0, то это слагаемое можно зачеркнуть.
Если в логической сумме одно из слагаемых равно 1, то сумма равна 1.
Пример
7.
Правило поглощения:
![]()
![]()
5
