
- •Оглавление:
- •Часть I. Определение симедианы
- •1.1 Определения и их эквивалентность
- •1.2 Симедиана и антипараллельность
- •1.3 Симедиана и ортоизогональ
- •1.4 Симедиана и подобие
- •1.5 Симедиана и изогональное сопряжение
- •Часть II. Основаная задача
- •2.1 Симедиана и инверсия
- •2.2 Основная задача и её применение
- •Часть III. Гармонический четырехугольник
- •3.1 Определение гармонического четырехугольника
- •3.2 Связь и симедианой и свойство
- •3.3 Задачи
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
- •1 Способ:
- •2 Способ:
Часть II. Основаная задача
2.1 Симедиана и инверсия
2.1.1 В окружности с центром О проведена хорда ВС. Через точку М – середину этой хорды проведен диаметр QW. Лучи МА и MD таковы, что СMA = СMD < 90 (А и D – точки пересечения этих лучей с окружностью лежат в одной полуплоскости относительно прямой QM).
А) Докажите, что одна из симедиан треугольника АВС лежит на прямой AD.
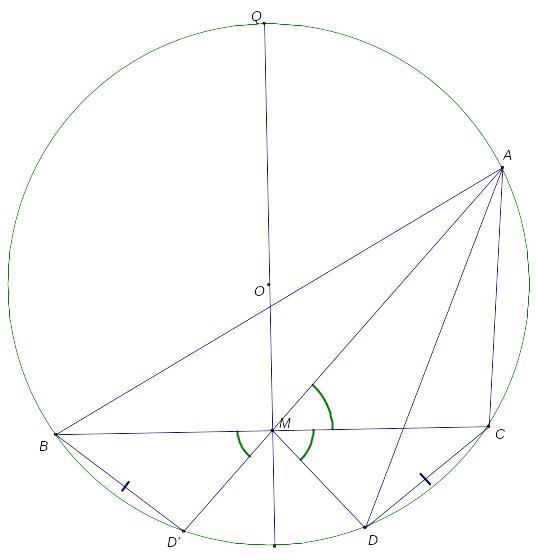
Доказательство:
Докажим,
что
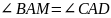 .
Продлим АМ
до пересечения с окружностью (см.рис).
Тогда точки D’
и D
симметричны относительно диаметра ОМ.
Следовательно, BD’
= CD,
то есть
,
что и требовалось.
.
Продлим АМ
до пересечения с окружностью (см.рис).
Тогда точки D’
и D
симметричны относительно диаметра ОМ.
Следовательно, BD’
= CD,
то есть
,
что и требовалось.
Ч.Т.Д.
Б) Докажите, что четырехугольник ОМDA – вписанный.
Доказательство:
Заметим,
что в дугах
∠AMD
= 2
 ∠AMC
=
∠AMC
=
 =
∠AOD.
Таким
образом, AOMD
– вписанный четырехугольник.
=
∠AOD.
Таким
образом, AOMD
– вписанный четырехугольник.
Ч.Т.Д.
В) Докажите, что все прямые AD, построенные описанным образом, пересекают прямую OM в одной и той же точке Р.
Г) Докажите, что OM·OP=R2, то есть М и Р – инверсны относительно данной окружности.
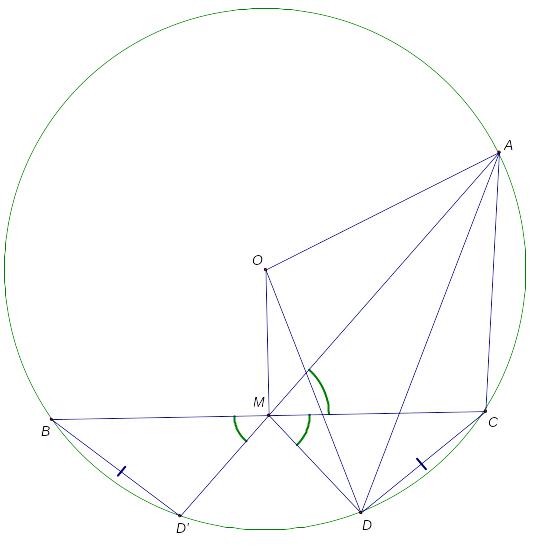
Доказательство:
Пусть P – образ точки М при инверсии относительно данной окружности (см. рис). Окружность, описанная около четырехугольника AOMD, переходит в прямую AD (поскольку точки A и D принадлежат окружности инверсии). Тогда точка P принадлежит прямой AD.
С другой стороны, точка P лежит на луче ОМ и не зависит от положения прямой AD. Следовательно, все прямые AD проходят через фиксированную точку P (образ точки М при инверсии относительно данной окружности).
Ч.Т.Д.
Комментарий: пункт В иногда называют теоремой о симметричной бабочке.
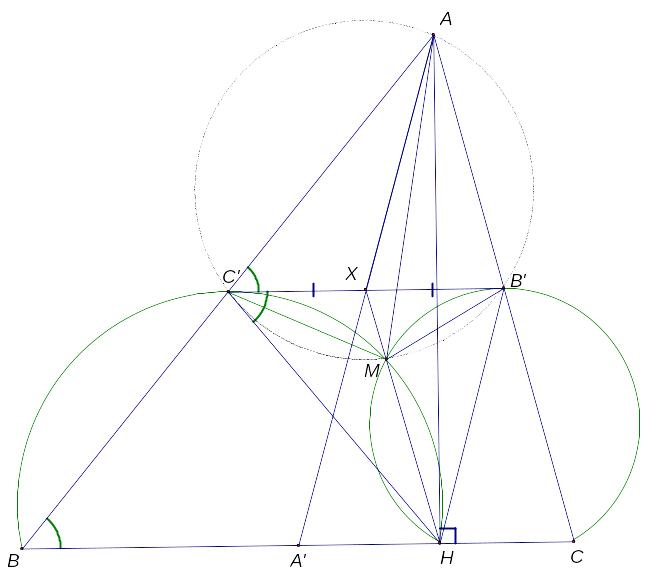
2.1.2 Точки A', B' и C' — середины сторон BC, CA и AB треугольника ABC соответственно, а AH — его высота.
А) (Международная олимпиада по математике, 1970) Докажите, что прямая MH проходит через середину C’B’.
Б) (Московская математическая олимпиада 2007) Докажите, что если описанные около треугольников BHC' и CHB' окружности проходят через точку M, отличную от H, то BAM=CAA'.
Доказательство:
1) Докажем, что AC’MB’ – вписанный. ∠AC’M = 180 – ∠BC’M = ∠MHB = 180 – ∠MHC = ∠MB’C = 180 – AB’M, следовательно AC’MB’ – вписанный, что и требовалось.
Поскольку мы пользовались только тем, что C’, B’ и H принадлежат сторонам треугольника, то доказано более общее утверждение: если взять точки B’, C’ и A’ на сторонах треугольника AC, AB и BC соответственно, то окружности, описанные около треугольников AB’C’ , BA’C’ и CA’B’ пересекаются в одной точке.
2) Докажем, что C’B’ – общая касательная для окружностей, описанных около треугольников BC’H и CB’H.
Заметим, что треугольники AC’B’ и B’C’H симметричны относительно C’B’. Из этого следует, что ∠HC’B’ = ∠B’C’A = ∠B’C’A. По теореме об угле между касательной и хордой C’B’ – касательная к окружности, описанной около треугольника BC’H. Для окружности описанной около CB’H доказательство аналогично.
3) MH – общая хорда, следовательно прямая MH пересекает общую касательную (C’B’) в середине [C’B’], таким образом, пункт А) доказан.
4) Теперь рассмотрим окружность AC’MB’: X – середина хорды C’B’, лучи XM и XA симметричны относительно C’B’. Из Задачи №2.1.1 следует, что AM – симедиана в треугольнике AC’B’, а следовательно, и в треугольнике ABC, так как эти треугольники гомотетичны с центром A.
Ч.Т.Д.
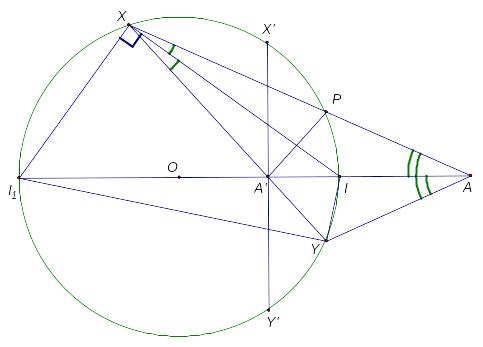
2.1.3 Точки А и A’ инверсны относительно окружности , причем A’ – внутри . Через A’ проводятся хорды XY. Докажите, что центры вписанной и одной из вневписанных окружностей треугольника AXY – фиксированы.
Доказательство:
Пусть I – точка пересечения AA’ с окружностью, а X’Y’ – хорда, проходящая через А’, перпендикулярная диаметру
1) Из того, что точки A’ и A инверсны, следует, что А – точка пересечения касательных из точек X’ и Y’. Из задачи №2.1.1 следует, что XP – симедиана в треугольнике XX’Y’. XA’– медиана, а XI – биссектриса в том же треугольнике, следовательно точки P и Y симметричны относительно I. Таким образом, AI - биссектриса в треугольнике AXY.
2) Таким образом, I – точка пересечения двух биссектрис в треугольнике AXY, следовательно I – инцентр данного треугольника, и он фиксирован, так как AA’ и окружность фиксированы, а значит, и их точка пересечения фиксирована.
3) Рассмотрим I1, диаметрально противоположную I. ∠I1XI = 90ᵒ, следовательно XI1 – биссектриса внешнего угла треугольника AXY. А AA’ – биссектриса внутреннего угла. Таким образом, I1 – точка пересечения биссектрис внешнего и внутреннего углов в треугольнике, значит I1 – центр вневписанной окружности у треугольника AXY.
Ч.Т.Д.
