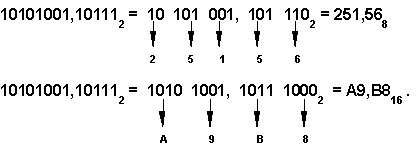Восьмеричная и шестнадцатеричная системы счисления
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина. Однако, чтобы профессионально использовать компьютер, следует научиться понимать слово машины. Для этого и разработаны восьмеричная и шестнадцатеричная системы.
Числа в этих системах читаются почти так же легко, как десятичные, требуют соответственно в три (восьмеричная) и в четыре (шестнадцатеричная) раза меньше разрядов, чем в двоичной системе (ведь числа 8 и 16 — соответственно, третья и четвертая степени числа 2).
Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему очень прост: достаточно каждую цифру заменить эквивалентной ей двоичной триадой (тройкой цифр) или тетрадой (четверкой цифр).
Перевод целых чисел из одной системы счисления в другую
Правило 1. Перевод числа x из системы счисления основанием P в систему счисления с основанием Q заключается в последовательном нахождении остатков от деления числа x на основание Q, при этом процесс продолжается до тех пор, пока частное от деления не будет меньше основания Q. Все вычисления выполняются в системе счисления с основанием P, т.е. основание Q должно также быть выражено в системе счисления с основанием P. Остатки от деления должны быть выражены цифрами системы счисления с основанием R. Представление искомого числа в системе счисления с основанием R получается выписыванием последнего частного и остатков от деления в обратном порядке.
На практике такой порядок перевода чисел используется при переводе из десятичной системы счисления в восьмеричную, шестнадцатеричную и двоичную. (Пример слайд)
Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
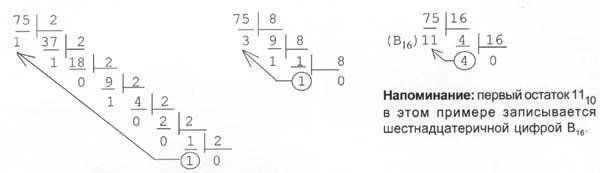
Ответ: 7510 = 1 001 0112 = 1138 = 4B16
Правило 2. Перевод числа x из системы счисления основанием P в систему счисления с основанием Q осуществляется путем представления числа х по степеням основания P. Все вычисления выполняются в системе счисления с основанием Q, т. е. основание P и цифры исходного числа должны также быть выражены в системе счисления с основанием Q.
На практике такой порядок перевода чисел используется при переводе из двоичной, восьмеричной и шестнадцатеричной системы счисления в десятичную.
Т.е. необходимо представить число в виде многочлена
x10 = an qn + an-1 qn-1 + ... + a0 q0 + a-1 q -1 + a-2 q-2 + ... + a-m q-m
и вычислить его средствами десятичной арифметики.
Примеpы:
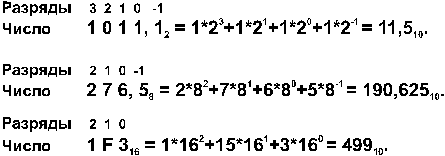
Правило 3. Перевод чисел из восьмеричной системы счисления в двоичную и наоборот переводится по триадам,
При переводе из восьмеричной системы в двоичную каждая цифра заменяется триадой, согласно табл.
При переводе из двоичной системы в восьмеричную число развивается на триады справа налево, недостающие цифры слева дополняются нулями. После этого, каждую триаду заменяют восьмеричной цифрой согласно табл.
Правило 4. Перевод чисел из шестнадцатеричной системы счисления в двоичную и наоборот переводится по тетрадам.
При переводе из шестнадцатеричной системы в двоичную каждая цифра заменяется тетрадой, согласно табл.2
Например: (слайд)
Чтобы перевести число из двоичной системы в восьмеричную или шестнадцатеричную, его нужно разбить влево и вправо от запятой на триады (для восьмеричной) или тетрады (для шестнадцатеричной) и каждую такую группу заменить соответствующей восьмеричной (шестнадцатеричной) цифрой.
Например, (слайд)
