Решение. Пусть случайное событие A – наудачу взятое число не делится ни на два, ни на три; случайное событие B – наудачу взятое число не делится на два или на три. Введём ещё два события: C – наудачу взятое число не делится на два; D – наудачу взятое число не делится на три. Тогда, очевидно, A = CD, B = C + D. События C и D независимы, так как и среди всех натуральных чисел и среди нечётных натуральных чисел два числа из идущих подряд трёх не

делятся на три, следовательно, P(A) = P(C)P(D) = 12 23 = 13 . Однако события C и D совместны,

поэтому P(B) = P(C) + .P(D) – P(CD) = P(C) + .P(D) – P(C)P(D) = 12 + 23 − 12 23 = 56 .

Пример 6. Абонент забыл последнюю цифру номера телефона и набирает её наудачу. Определить вероятность того, что он наберёт нужный номер не более, чем за три попытки.

Решение. Случайное событие A – абонент дозвонился не более, чем за три попытки набора номера. Пусть случайное событие Ai – абонент дозвонился при i-ом наборе номера (i = 1, 2, 3). Так как каждый следующий набор номера производится только в том случае, если предыдущая попытка оказалась неудачной, то

A = A1 + A 1A2 + A 1 A 2A3.

Здесь события-слагаемые несовместны, а события-сомножители зависимы, поскольку при каждом следующем наборе номера абонент учитывает результат предыдущих попыток. Значит,

P(A) = P(A1) + P( A 1)P(A2 / A 1) + P( A 1) P( A 2 / A 1)P(A3 / A 1 A 2) = 101 +109 19 +109 89 81 = 103 .

Вероятность события A можно также найти, вычислив сначала вероятность противоположного события A и использовав формулу P(A) = 1 – P( A ).

Случайное событие A – абонент не дозвонился за три набора номера – есть произведение трёх событий: A = A 1 A 2 A 3, поэтому

P( A ) = P( A 1) P( A 2 / A 1)P( A 3 / A 1 A 2) = 109 89 78 = 107 .

Но тогда P(A) = 1 – 0,7 = 0,3.

Пример 7. Вероятность попадания в мишень при одном выстреле у каждого из двух стрелков равна 0,3. Стрелки стреляют по очереди, причём каждый может сделать по два выстрела. Попавший в мишень первым получает приз. Найти вероятности получения приза для каждого из стрелков и вероятность того, что приз будет вручён стрелкам. Какова вероятность того, что приз останется у организаторов соревнования?

Решение. Обозначим события, вероятности которых следует определить.

A – приз будет вручён первому стрелку;

B – приз будет вручён второму стрелку;

C – приз будет вручён стрелкам;

C – приз останется у организаторов соревнования. Введём также события:

Ai – первый стрелок попал в мишень при i-ом выстреле;

Bi – второй стрелок попал в мишень при i-ом выстреле (i = 1, 2). Тогда можно записать:

A = A1 + A 1 B 1A2; B = A 1B1 + A 1 B 1 A 2B2; C = A + B.

События-слагаемые во всех случаях – несовместные события, а события-сомножители – независимые события, так как вероятность попадания в мишень каждым из стрелков не зависит ни от номера выстрела, ни от результата предыдущего выстрела. Таким образом:

P(A) = P(A1) + P( A 1)P( B 1)P(A2) = 0,3 + 0,7 0,7.0,3 = 0,447;

P(B) = P( A 1)P(B1) + P( A 1)P( B 1)P( A 2)P(B2) = 0,7 0,3 + 0,7 0,7 0,7 0,3 = 0,7 P(A) = 0,3129;

P(C) = P(A) + P(B);

P( C ) = 1 – P(C) = 0,2401.

Вероятность события C можно найти иначе, именно: C = A 1 B 1 A 2 B 2, поэтому

P( C ) = P( A 1)P( B 1)P( A 2)P( B 2) = 0,74 = 0,2401.

Пример 8. В ящике находятся 6 катушек белых, 4 катушки чёрных и 2 катушки красных ниток. Катушки извлекаются по одной без возвращения. Определить вероятность того, что катушка с белыми нитками появится раньше, чем катушка с чёрными нитками.

Решение. По условию задачи после появления катушки с белыми нитками извлечения прекращаются, после появления катушки с красными нитками проводится следующее извлечение, катушка с чёрными нитками не должна появляться. Если A – случайное событие – катушка с белыми нитками появилась раньше, чем катушка с чёрными нитками, то

A = A1 + C1A2 + C1C2A3,

где Ai – появление катушки с белыми нитками при i-ом извлечении (i = 1, 2, 3), Ci – появление катушки с красными нитками при i-ом извлечении (i = 1, 2). Здесь события-слагаемые – несовместные события, а события-сомножители – зависимые события, так как катушки извлекаются без возвращения и возможность извлечь катушку какого-то конкретного цвета зависит от результатов предыдущих извлечений. Поэтому

P(A) = P(A1) + P(C1)P(A2 /C1) + P(C1)P(C2 /C1)P(A3 /C1C2) = 126 +122 116 +122 111 106 = 53 .

Пример 9. Из урны, содержащей 6 белых и 4 чёрных шара, наудачу последовательно извлекается по одному шару до первого появления чёрного шара. Найти вероятность того, что придётся производить четвёртое извлечение, если извлечения шаров производятся: а)с возвращением шаров в урну; б)без возвращения шаров в урну.

Решение. Случайное событие A – будет производиться четвёртое извлечение. Ясно, что четвёртое извлечение будет производиться в том случае, если при первых трёх извлечениях не появится чёрный шар. Обозначим через Ai случайное событие – при i-ом извлечении появился шар белого цвета (i = 1, 2, 3). Тогда A = A1A2A3, следовательно, P(A) = P(A1A2A3).

а)В этом случае шары извлекаются с возвращением, поэтому вероятность извлечения белого шара в очередной раз не зависит от результатов предыдущих извлечений, поэтому события Ai независимы и

P(A) = P(A1)P(A2)P(A3) = 0,63 = 0,216.

б)Если шары извлекаются без возвращения, то после каждого извлечения состав урны изменяется, следовательно, изменяются и вероятности извлечения шаров. События Ai в этом случае зависимы, поэтому

P(A) = P(A1)P(A2 / A1)P(A3 / A1A2) = 106 95 84 = 16 ≈ 0,167.

Пример 10. Сколько нужно взять чисел из множества натуральных чисел, чтобы с вероятностью не менее 0,9 быть уверенным, что среди этих чисел будет хотя бы одно чётное? Изменится ли необходимое количество чисел, если выбирать их из множества чисел, кратных трём?

Решение. Здесь случайное событие A – среди n взятых наудачу натуральных чисел есть хотя бы одно чётное. Подберём n из условия P(A) ≥ p = 0,9, которое равносильно условию

P( A ) < 1 – p. Событие A – среди n взятых наудачу натуральных чисел чётных нет. Пусть Ai – i-ое натуральное число – чётное. Тогда A = A 1 A 2… A n. Ясно, что для любого i P( A i) = 1/2 и

что события A i – независимые. Тогда P( A ) = P( A 1)P( A 2) . . . P( A n) = (1/2)n < 0,1, откуда

n > ln 0,1 / ln 0,5 ≈ 3,32. Таким образом, с уверенностью 0,9 достаточно взять четыре произвольных натуральных числа. Это необходимое количество чисел n = 4 не изменится, если числа выбирать из множества чисел, кратных трём, так как вероятность того, что наудачу взятое кратное трём число будет чётным, также равна 1/2.

Пример 11. Студент знает 20 из 25 вопросов программы. Зачёт считается сданным, если студент ответит не менее чем на три из четырёх предложенных ему вопросов. Какова вероятность того, что: а)студент сдаст зачёт; б)зачёт будет сдан, если известно, что на первые два вопроса студент уже ответил.

Решение. Обозначим случайные события: A – студент сдал зачёт; A1 – студент ответил на четыре вопроса; A2 – студент ответил на три вопроса; B – студент ответил на первые два из четырёх вопросов.

а)В этом случае A = A1 + A2, события A1 и A2 – несовместные, поэтому, применяя для подсчёта вероятностей событий A1 и A2 классическое определение вероятности, имеем:

б)В этом случае рассуждения аналогичны, только требуется найти условную вероятность события A при условии, что событие B произошло, поэтому

Пример 12. Общество, состоящее из n мужчин и 2n женщин, наудачу разбивается на n групп по три человека в каждой группе. Найти вероятность того, что в каждой группе будет по одному мужчине.

Решение. Здесь случайное событие A – общество из 3n человек разбито на n групп должным образом – есть произведение случайных событий Ai – i-ая группа состоит из одного мужчины и двух женщин (i = 1, 2, . . . , n), т. е., A = A1A2 . . . An . Но так как образование каждой следующей группы происходит из контингента, оставшегося после образования предыдущих групп, то события Ai будут зависимыми, поэтому

P(A) = P(A1)P(A2/A1)P(A3/A1A2) . . . P(An/A1A2 . . . An-1) =

Пример 13. Игрок A поочерёдно играет с игроками B и C, имея вероятность выигрыша в

каждой партии 2/3, и прекращает игру после первого проигрыша или после двух сыгранных с каждым игроком партий. Определить вероятности выигрыша игры игроками A, B и C.

Решение. Обозначим через A, B, C события – выигрыш игры игроком A, B, C соответственно и через Bi , Ci события – выигрыш игроком B или C i-ой партии (i =1 ,2). Так как выигрыш партии каждым из игроков B или C означает проигрыш партии и, следовательно, остановку игры ведущим её игроком A, то случайные события A, B, C можно записать в виде:

A = B 1 C 1 B 2 C 2 ; B = B1 + B 1 C 1B2 ; C = B 1C1 + B 1 C 1 B 2C2 .

Здесь события-слагаемые будут несовместными, а события-сомножители – независимыми событиями, поэтому

P(A) = P( B 1)P( C 1)P( B 2)P( C 2) = 23 23 23 23 = 1681 ;

P(B) = P(B1) + P( B 1)P( C 1) P(B2) = 13 + 23 23 13 = 1327 ;

P(C) = P( B 1)P(C1) + P( B 1)P( C 1)P( B 2) P(C2) = 23 13 + 23 23 23 13 = 2681 .

Замечание. Так как события A, B, C образуют полную группу (A + B + C = U) и попарно несовместны, то P(A + B + C) = P(A) + P(B) + P(C) =1, поэтому вероятность одного из событий, например C, можно было найти так: P(C) = 1 – P(A) – P(B) = 1 – 1681 – 1327 = 2681 .

Пример 14. Двое игроков поочерёдно бросают монету. Выигрывает тот из них, у кого раньше появится герб. Определить вероятности выигрыша для каждого из игроков.

Решение. Обозначим через Ai и Bi события – появление герба у первого и второго игроков при их i-ом бросании (i =1, 2, . . . ), а через A и B события – выигрыши первого и второго игроков. Тогда

A = A1 + A 1 B 1A2 + A 1 B 1 A 2 B 2A3 + . . .;

B = A 1B1 + A 1 B 1 A 2B2 + A 1 B 1 A 2 B 2 A 3B3 + . . .

Ясно, что все события-слагаемые – несовместные события, а события-сомножители – независимые. Так как P(Ai) = P(Bi) = 1/2, то получаем, что вероятности выигрыша каждого из игроков являются суммами членов бесконечно убывающей геометрической прогрессии:

Формула полной вероятности. Формула Байеса.

Предположим, что событие A может наступить только вместе с одним из нескольких попарно несовместных событий H1, H2, . . . , Hn, образующих полную группу. Условимся называть события Hi (i = 1, 2, … , n) гипотезами (по отношению к событию A). Имеет место следующая формула

P(A)= ∑n P(Hi ) P(A/Hi )= P(H1 ) P(A/H1 )+P(H 2 ) P(A/H 2 )+...+P(H n ) P(A/H n ),

i=1

P(A/Hi) – условная вероятность события A при условии осуществления гипотезы Hi.

В тесной связи с формулой полной вероятности находится формула Байеса (Томас Байес, 1702-1761, английский учёный). Она работает в той же ситуации, что и формула полной

вероятности (событие A может наступить только вместе с одним из нескольких попарно несовместных событий H1, H2, . . . , Hn). Если до опыта вероятности гипотез были P(H1), P(H2), .

. . , P(Hn), а в результате опыта появилось событие A, то можно найти «новые», т. е., условные вероятности гипотез P(H1/A), P(H2/A), . . . , P(Hn/A) по формуле Байеса:

i=1

Таким образом, формулы Байеса дают возможность «пересмотреть» вероятности гипотез, зная результат опыта.

Пример 1. Имеются три урны. В первой урне находятся 5 белых и 3 чёрных шара, во второй – 4 белых и 4 чёрных шара, а в третьей – 8 белых шаров. Наугад выбирается одна из урн (это может означать, например, что осуществляется выбор из вспомогательной урны, где находятся три шара с номерами 1, 2 и 3). Из этой урны наудачу извлекается шар. Какова вероятность того, что он окажется чёрным?

Решение. Событие A – извлечён чёрный шар. Шар может быть извлечён или из первой урны (гипотеза H1), или из второй (гипотеза H2), или из третьей (гипотеза H3). Так как имеются одинаковые шансы выбрать любую из урн, то P(H1) = P(H2) = P(H3) = 1/3. Далее находим вероятности события A при каждой из гипотез: P(A/H1) = 3/8, P(A/H2) = 4/8 = 1/2, P(A/H3) = 0/8 =0. Отсюда следует, что

P(A) = P(H1)P(A/H1) + P(H2)P(A/H2) + P(H3)P(A/H3) = 13 83 + 13 12 + 13 0 = 81 + 16 = 247 .

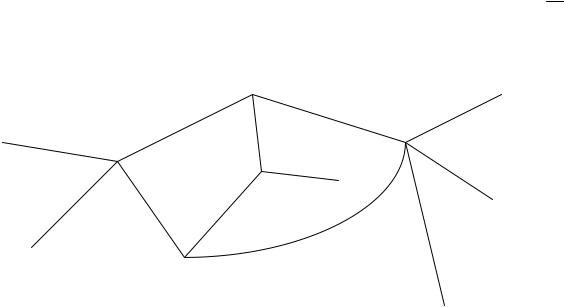
Пример 2. На рисунке изображена схема дорог.

O

B1

B3

B2

M

Туристы выходят из пункта O, выбирая наугад на разветвлении дорог один из возможных путей. Какова вероятность того, что туристы попадут в пункт M?

Решение. Как видно из рисунка, путь туристов обязательно проходит через один из промежуточных пунктов B1, B2, B3. Пусть Hi – событие, состоящее в том, что при своём движении туристы попадут в пункт Bi (i = 1, 2, 3).События H1, H2, H3 по условию несовместны и равновероятны: ведь путь из точки O выбирается наугад. Поэтому P(H1) = P(H2) = P(H3) =1/3. Если A – событие: туристы попадут в пункт M, то P(A/H1) = 1/3, P(A/H2) = 1/2, P(A/H3) =1/4. Искомую вероятность находим по формуле полной вероятности.

P(A) = P(H1)P(A/H1) + P(H2)P(A/H2) + P(H3)P(A/H3) = 13 13 + 13 12 + 13 14 = 1336 .

Пример 3. Электролампы изготавливаются на трёх заводах. Первый завод производит 30% общего количества электроламп, второй – 25%, а третий – остальную часть. Продукция первого завода содержит 1% бракованных электроламп, второго – 1,5%, третьего – 2%. В магазин поступает продукция всех трёх заводов. Купленная в магазине лампа оказалась бракованной. Какова вероятность того, что она произведена первым заводом?

Решение. Введём обозначения для событий: A – купленная электролампа оказалась бракованной; Hi – лампа изготовлена i-м заводом (i = 1, 2, 3). Имеем: P(H1) = 0,30; P(H2) = 0,25; P(H3) = 0,45; P(A/H1) = 0,01; P(A/H2) = 0,015; P(A/H3) = 0,02. Искомую вероятность P(H1/A)

находим по формуле Байеса.

Здесь вероятность события A в знаменателе найдена по формуле полной вероятности. Пример 4. При обследовании больного имеется подозрение на одно из двух заболеваний

H1 и H2. Их вероятности в данных условиях P(H1) = 0,6, P(H2) = 0,4. Для уточнения диагноза назначается анализ, результатом которого является положительная или отрицательная реакция. В случае болезни H1 вероятность положительной реакции равна 0,9, отрицательной – 0,1, а в случае болезни H2 положительная и отрицательная реакции равновероятны. Анализ провели дважды, и оба раза реакция оказалась положительной (событие A). Требуется найти вероятность каждого заболевания после проделанных анализов.

Решение. Условная вероятность того, что в случае заболевания H1 произойдёт событие A

(т.е. дважды при анализе реакция окажется отрицательной) P(A/H1) = 0,1 0,1 = 0,01, а в случае заболевания H2 имеем P(A/H2) = 0,5 0,5 = 0,25. Применяя формулу Байеса, получаем:

Отсюда видно, что полученные результаты анализов дают веские основания предполагать болезнь H2.

Пример 5. По линии связи с вероятностями 0,84 и 0,16 соответственно передаются два сигнала A и B. Из-за помех 1/6 часть переданных сигналов A искажается и принимается как сигнал B, а 1/8 часть переданных сигналов B принимается как сигнал A. 1)Какова вероятность того, что при приёме появится: а)сигнал A; б)сигнал B? 2)Известно, что принят сигнал A. Какова вероятность того, что он же и был передан?

Решение. Введём обозначения для событий. H1 – передан сигнал A, H2 – передан сигнал B, A – при приёме появится сигнал A, B – при приёме появится сигнал B. Имеем: P(H1) = 0,84; P(H2) = 0,16; P(A/H1) = 5/6; P(A/H2) = 1/8; P(B/H1) = 1/6; P(B/H2) = 7/8.

1)По формуле полной вероятности находим:

Пример 6. Клеточная активность мозга регистрируется микроэлектродом. С вероятностью 0,6 предполагается, что в опыте наблюдается первая из двух соседних структур мозга. Известно, что в первой структуре 60% всех клеток, а в соседней 50% продуцируют некоторый тип активности. Микроэлектрод зарегистрировал в фиксированный момент данный тип активности. Как в связи с этим наблюдением изменится мнение о нахождении микроэлектрода в первой структуре мозга?

Решение. Введём обозначения для событий. H1 – микроэлектрод находится в первой структуре мозга; H2 – микроэлектрод находится во второй структуре мозга; A – зарегистрирован данный тип активности. Имеем: P(H1) = 0,6; P(H2) = 0,4; P(A/H1) = 0,6; P(A/H2)

Вероятность гипотезы H1 возросла.

Пример 7. Два из трёх независимо работающих элементов вычислительного устройства отказали. Найти вероятность того, что отказали первый и второй элементы, если вероятности отказа первого, второго и третьего элементов соответственно равны p1 = 0,2; p2 = 0,4; p3 = 0,3.

Решение. Введём обозначение A для события – отказали два элемента. Можно сделать следующие предположения (гипотезы):

H1 – отказали первый и второй элементы, а третий элемент исправен, при этом (поскольку элементы работают независимо, то применима теорема умножения вероятностей) P(H1) =

p1.p2.(1 – p3) = 0,2 0,4 0,7 = 0,056;

H2 – отказали первый и третий элементы, а второй элемент исправен, при этом P(H2) = p1.p3.(1 – p2) = 0,2 0,3 0,6 = 0,036;

H3 – отказали второй и третий элементы, а первый элемент исправен, при этом P(H3) = p2.p3.(1 – p1) = 0,4 0,3 0,8 = 0,096.

Возможны ещё следующие предположения: H4 – ни один элемент не отказал;

H5 – отказал только один элемент;

H6 – отказали все три элемента –

но из условия задачи следует, что P(A/H4) = 0, P(A/H5) = 0, P(A/H6) = 0, следовательно, равны нулю и произведения P(H4)P(A/H4), P(H5)P(A/H5), P(H6)P(A/H6).

При гипотезах H1, H2, H3 событие A достоверно, соответствующие условные вероятности равны единице. По формуле полной вероятности находим вероятность события A.

6

P(A) = ∑P(Hi ) P(A/Hi ) = P(H1)P(A/H1) + P(H2)P(A/H2) + P(H3)P(A/H3) =

i =1

= 0,056 1 + 0,036 1 + 0,096 1 = 0,188.

Теперь искомую вероятность вычисляем по формуле Байеса.

Пример 8. Имеются три партии деталей по 20 деталей в каждой. Число стандартных деталей в партиях соответственно равно 20, 15 и 10. Из наудачу выбранной партии наудачу извлечена деталь, оказавшаяся стандартной. Деталь возвращают в партию и вторично наудачу извлекают деталь, которая также оказывается стандартной. Найти вероятность того, что детали извлечены из третьей партии.

Решение. Обозначим через A событие – в каждом из двух испытаний (с возвращением) была извлечена стандартная деталь. Можно выдвинуть три гипотезы: Hi – детали извлекались

из i-ой партии (i =1, 2, 3). Так как детали извлекались из наудачу взятой партии, то вероятности гипотез одинаковы: P(Hi) = 1/3 (i = 1, 2, 3). Далее находим условные вероятности: P(A/H1) = 1 (в первой партии все детали стандартные, поэтому вероятность того, что из первой партии

будут последовательно извлечены две стандартные детали, равна единице); P(A/H2) = 1520 1520 =

Пример 9. Батарея из трёх орудий произвела залп, причём два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны p1 = 0,4; p2 = 0,3; p3 = 0,5.

Решение. Обозначим через A событие – два орудия попали в цель. Выдвинем две гипотезы: H1 – первое орудие попало в цель; H2 – первое орудие не попало в цель. По условию P(H1) = 0,4, следовательно, P(H2) = 1 – 0,4 = 0,6 (событие H2 противоположно событию H1).

Если событие A наступило при осуществлении гипотезы H1, то это означает, что вместе с первым орудием в цель попало либо второе орудие, а третье не попало, либо, наоборот, третье орудие попало в цель, а второе не попало. Применяя теоремы сложения и умножения вероятностей, получаем:

P(A/H1) = p2(1 – p3) + p3(1 – p2) = 0,3 0,5 + 0,5 0,7 = 0,5.

Если событие A наступило при осуществлении гипотезы H2, то это означает, что первое орудие дало промах, а в цель попали снаряды второго и третьего орудий, поэтому

Пример 10. Из урны, содержащей 3 белых и 2 чёрных шара, переложено 2 шара в урну, содержащую 4 белых и 2 чёрных шара. Найти вероятность вынуть после этого из второй урны белый шар.

Решение. Обозначим через A событие – из второй урны вынут белый шар. Можно выдвинуть три гипотезы: H1 – из первой урны во вторую переложены два белых шара; H2 – переложены один белый и один чёрный шары; H3 – переложены два чёрных шара. Имеем: