

Все эти распределения, очевидно, образуют полную
элементарных событий. Ясно, что |A|=1. Поэтому P(A) = |
1 |
|
CnN+-1N-1 |
||
|
группу равновозможных
= n!(N −1)! . Событию B (n + N −1)!
благоприятствуют те распределения, при которых в каких-либо n ячейках находится ровно по одной частице. Порядок n ячеек не имеет значения, так как частицы неразличимы. Поэтому
| B |= Cn |
и P(B) = |
Cn |
|
. Вероятности P(A) и P(B) называются статистиками Бозе- |
N |
|
|||
CnN+−N1 |
|
|||
N |
|
−1 |
||
Эйнштейна.
Пример 12. (Статистики Ферми-Дирака.)
Как и раньше, имеется N различимых ячеек и n ≤ N неразличимых частиц. Согласно физической модели Ферми-Дирака, в каждой ячейке может находиться не более одной частицы т.е. или 0, или 1 частица. При этом все такие распределения n частиц по N ячейкам объявляются равновозможными. Найти вероятность того, что: 1)частицы будут находиться в определенных n ячейках; 2)частицы будут находиться в каких-либо n ячейках.
Решение. Событие A – частицы находятся в определенных n ячейках. Событие B – частицы находятся в каких-либо n ячейках. Элементарным событием объявляется любое распределение n неразличимых частиц по N ячейкам, при котором в каждой ячейке находится не более одной частицы. Очевидно, число таких распределений | Ω |= CnN , множество этих распределений образует полную группу и, согласно физической модели Ферми-Дирака, все они
равновозможны. Далее очевидно, что |A|=1, поэтому P(A) = 1 ; поэтому
CnN
Cn P(B) = N =1.
CnN
Итак, мы видим, что вероятности меняются в зависимости от выбора физической модели.
Замечание. В литературе зачастую применяются следующие обозначения: множество всех элементарных исходов Ω = n ; множество элементарных исходов, благоприятствующих событию A, A = m .
Геометрическое определение вероятности
Пусть G – борелевское множество в R n , n ≥1, для которого 0 < mesG < ∞ , подобласть
D G, D – борелевское множество. Рассматривается следующий эксперимент: наудачу

берется точка из G (другой вариант: наудачу бросается точка на G). При этом точка может случайным образом попасть в D. Геометрическое определение вероятности утверждает, что вероятность попадания точки в D выражается равенством
P(D) = mesD . mesG
Здесь D = G – достоверное событие, D = – невозможное событие. Очевидно 0 ≤ P(D) ≤ 1.
В отличие от классического определения вероятности из того, что P(D)=1, не следует, что D = G, т.е. что D – достоверное событие. Действительно, пусть D совпадает с G без одной точки. Тогда D не является достоверным событием, хотя P(D) = 1. Аналогично, из того, что
P(D) = 0, не следует, что D = , т.е. что D – невозможное событие. Например, если D состоит из одной точки, то mesD = 0 , P(D) = 0, но D не является невозможным событием. Будем обозначать противоположное событие G\D через D . Как и при классическом определении вероятности P(D) =1 - P(D).
Пример 1. В круг радиуса R наудачу бросается точка. Какова вероятность, что взятая точка окажется от центра круга на расстоянии, большем, чем R/2?
Решение. Эксперимент состоит во взятии наугад точки в круге радиуса R. Значит, G совпадает с множеством точек круга радиуса R. Элементарным событием является точка круга радиуса R, mesG =πR 2 , 0 < рR 2 < ∞. D – множество точек круга G, отстоящих от центра круга
на расстояние, большее, чем |
|
R/2; |
mesD = πR 2 − π(R/2)2 |
= 3рR 2 / 4. |
По |
геометрическому |
|||||||||||||||||
определению вероятности P(D) = |
|
3рR 2 |
|
= |
3 . |
|
|
|
|
|
|
|
|
|
|
||||||||
|
4 рR 2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример 2. На горизонтальном диаметре круга радиуса R наугад берется точка. Затем |
||||||||||||||||||||||
через эту точку проводится хорда, |
перпендикулярная диаметру. Найти вероятность того, что |
||||||||||||||||||||||
длина хорды не превосходит R. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
′ |
′ |
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 6 |
(см. |
|
|
|
|
|
|
|
|
|
|
||||||
|
Решение. Угол AOB= A OB |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
рис.1). Эксперимент состоит во взятии наудачу |
A′ |
|
|
|
|
A |
|||||||||||||||||
точки из интервала (−R, R) , следовательно, G = |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||
(−R, R) , а mesG = 2R . Так |
как |
|
AOB= |
р |
, то |
|
|
|
|
|
|
|
|
|
|
||||||||
|
6 |
− R |
B′ |
|
|
0 |
|
B |
|
|
R |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
длина |
отрезка AB |
равна |
R |
и, |
|
следовательно, |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хорда, |
проходящая |
через |
A |
и |
B, |
равна |
|
R. В |
|
|
|
|
|
|
|
|
|
|
|||||
Рис.1

качестве D берем [B, R] U[−R, B′]. Длина вертикальной хорды не превосходит R тогда и только
тогда, когда наудачу взятая точка из G попадет в D. Так как mesD = 2R − 2Rcos |
р |
= 2R − R 3 , |
|||
|
|
|
|
6 |
|
то по геометрическому определению вероятности P(D) = 2R − R 3 |
=1 − |
3 |
≈ 0.15. |
|
|
2R |
|
2 |
|
|
|
Пример 3. На верхней полуокружности радиуса R наудачу берется точка. Затем через эту точку проводится хорда, перпендикулярная горизонтальному диаметру. Какова вероятность, что длина хорды не превосходит R?
Решение. Испытание состоит во взятии наугад точки из верхней полуокружности радиуса R. Значит, G образовано множеством точек верхней полуокружности; mesG = рR , 0<
πR< ∞.
Обозначим через D объединение двух дужек (см. рис. 1): RA и (–R)A. Длина искомой хорды не превзойдет R тогда и только тогда, когда наудачу взятая точка, через которую
проводится вертикальная хорда, содержится в D. Так как mesD = 2 р6 R = р3R , то искомая
вероятность находится по геометрическому определению и имеет значение рR
P(D) = р3R = 13 ≈ 0.33.
Может показаться, что пример 2 и пример 3 одинаковы, так как точки горизонтального диаметра находятся во взаимно однозначном соответствии с концами вертикальных хорд, проходящих через них, лежащих на верхней полуокружности. Иными словами, на первый взгляд, два различных способа решения приводят к различным ответам. На самом деле, две последние задачи совершенно различны, так как речь в них идет о различных испытаниях. В примере 2 наудачу берутся точки горизонтального диаметра, через которые проводят хорды, а в примере 3 испытание состоит во взятии наудачу точек верхней полуокружности, через которые проводят хорды.
Пример 4. (Задача о встрече.) Двое договариваются о встрече в определенном месте, которая должна произойти в промежутке времени от нуля до часа. Каждый из договаривающихся приходит к месту встречи в любой наугад взятый момент времени из промежутка [0, 1] и ждет другого 20 минут (в пределах указанного промежутка времени). Какова вероятность, что встреча состоится?
Решение. Обозначим через x момент прихода первого лица, через y – момент прихода второго лица. По условию 0 ≤ x ≤1, 0 ≤ y ≤1, x, y принимают указанные значения независимо друг от друга. Эксперимент состоит в приходе двух лиц к месту встречи. Элементарным
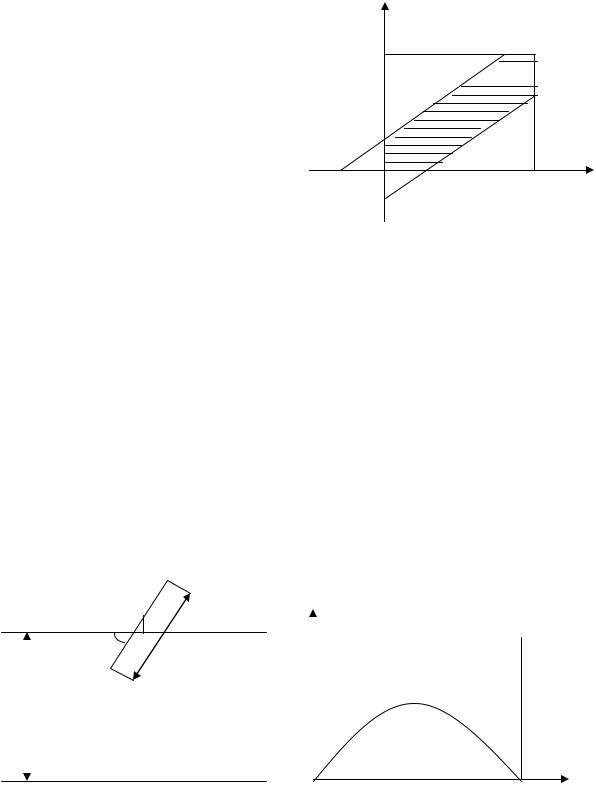
событием является упорядоченная пара (x, y), т.е. точка плоскости. Эти точки заполняют единичный квадрат G, Наш эксперимент мы отождествляем с экспериментом, состоящим во взятии точки из G. Встреча состоится тогда и только тогда, когда
y
1
G
D
1
3
| x − y | ≤ |
1 |
, |
x, y G . |
Множество точек, |
− |
1 |
|
0 |
1 |
1 |
x |
||
3 |
|
3 |
− |
1 |
3 |
|
|
||||||
|
|
|
|
|
|
|
|
3 |
Рис.2 |
|
|
||
удовлетворяющих |
последнему |
условию, |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||||
обозначим |
|
через |
D. |
Изобразим |
эту область |
D. |
|
Область |
D является |
частью |
квадрата, |
||
заключенной между прямыми y = x ± 13 (см. рис.2). Мера D равняется площади квадрата минус сумма площадей двух треугольников, отсекаемых от квадрата указанными прямыми. Соединив
два |
треугольника |
|
гипотенузами, получим квадрат |
со стороной |
2 |
. Следовательно, |
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
mesD |
|
|
2 |
2 |
= |
5 |
. |
По геометрическому определению |
вероятности |
искомая вероятность |
||
|
=1- |
3 |
|
9 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
5 |
|
|
|
|
|
|
|
|
|
|
|
|
p = |
9 |
|
= 5 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
9 |
|
|
|
|
|
|
|
|
|
||
Пример 5. (Задача Бюффона.) Плоскость разграфлена параллельными прямыми, отстоящими друг от друга на расстоянии 2а. На плоскость наудачу бросается игла длины 2l ,
ϕ |
x |
a |
|
|
|
||
|
|
||
|
|
2l |
|
|
|
|
G |
2a |
|
|
x = l sin ϕ |
|
|
|
|
|
0 |
D |
|
|
Рис.4 |
π ϕ |
|
Рис.3 |
|
||
|
|
(l < a) . Найти вероятность того, что игла пересечет какую-нибудь прямую.

Решение. Обозначим через ϕ угол, который игла образует с параллельными прямыми
(0 ≤ ϕ < π) , через x − расстояние от середины упавшей иглы до ближайшей к ней параллельной прямой, 0 ≤ x ≤ a (см. рис. 3). Множество точек (ϕ, x)образует прямоугольник G декартовой плоскости (см. рис.4), mesG = aπ . Эксперимент, состоящий в бросании наудачу иглы на плоскость, отождествляется с экспериментом, состоящим во взятии точки (ϕ, x) из области G.
Игла пересечется с одной из параллельных прямых тогда и только тогда, когда будет выполняться неравенство x ≤ l sin ϕ. Последнее неравенство задает область D G,
|
|
|
|
|
|
|
|
|
|
π |
|
|
|
|
|
|
|
|
|
0π = 2l. |
|
|
|||
|
|
|
|
|
|
|
|
|
mesD = ∫l sin ϕdϕ = −l cosϕ |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из этого следует, что искомая вероятность |
p = |
|
|
2l |
. |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aπ |
|
|
||||||||
Пример 6. Отрезок длины l ломается в двух наугад взятых точках. Какова вероятность |
|||||||||||||||||||||||||
того, что из трех полученных отрезков можно построить треугольник? |
|
|
|||||||||||||||||||||||
Напомним, что из трех отрезков |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
можно построить треугольник тогда и только |
|
|
y |
|
|
||||||||||||||||||||
тогда, |
когда |
сумма |
длин |
|
любых двух |
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
||||||
отрезков больше длины третьего. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Решение. Обозначим концы отрезка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
длины |
l через M и N . Через x обозначим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
расстояние от |
M до первой |
точки |
излома, |
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
через y − расстояние между двумя точками |
2 |
|
|
|
|
|
|
D |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
излома. |
Очевидно |
x ≥ 0, |
y ≥ 0, |
x + y ≤ l . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Обозначим через G область, задаваемую |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
этими |
неравенствами. |
Ее |
границами |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|||||||
0 |
|
|
|
|
|
l |
|
x |
|||||||||||||||||
являются оси x = 0, |
y = 0 и прямая x + y = l . |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
||||||||||||||||
G представляет |
собой |
прямоугольный |
|
|
|
|
|
|
|
|
|
Рис.5 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
равнобедренный |
треугольник |
с |
катетом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
длины l; mesG |
= |
l 2 |
. Эксперимент состоит в изломе отрезка длины l |
в двух точках наудачу. |
|||||||||||||||||||||
|
|||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы этот эксперимент отождествим с экспериментом, состоящим во взятии точки из области G. Полученные три отрезка имеют длины x, y, l −(x + y) . Из этих отрезков можно составить треугольник тогда и только тогда, когда выполняются условия

|
|
x + y > l −(x + y), |
x |
+ y > |
|
l |
, |
|
|
|
||||||||
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
x < |
|
l |
|
|
|
|
|
|
|
|
|
|
x +l −(x + y) > y; что равносильно условиям |
|
|
, |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
||||
|
|
y +l - (x + y) > x, |
|
y < |
. |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||
Обозначим через D область, задаваемую этими неравенствами (см. рис. 5). Область D |
||||||||||||||||||
представляет собой равнобедренный прямоугольный треугольник с катетом длины |
l |
|
. Поэтому |
|||||||||||||||
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
mesD = l 2 |
|
|
|
|
l2 |
= 1 . |
|
|
|
|
|
|
|
|
|
|
||
и искомая вероятность p = |
8 |
|
|
|
|
|
|
|
|
|
|
|
||||||
l2 |
|
|
|
|
|
|
|
|
|
|
||||||||
8 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 7. Какова вероятность того, что из трех взятых наудачу отрезков длины не |
||||||||||||||||||
больше l можно построить треугольник? |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Решение. Обозначим длины этих отрезков через x, y, z. Имеем 0 < x ≤ l, 0 < y ≤ l, |
||||||||||||||||||
0 < z ≤ l. Обозначим через G множество |
z |
|
|
|
|
|
|
|
|
|
|
|||||||
точек с координатами |
(x, y, z), |
для |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
которых |
0 < x ≤ l, 0 < y ≤ l, 0 < z ≤ l − |
l |
|
|
|
|
|
|
|
|
|
|
||||||
куб в трехмерном пространстве с ребром |
|
|
|
|
|
|
|
|
|
|
|
|||||||
длины |
l, mesG = l 3 . |
Эксперимент |
|
|
|
|
|
|
|
|
|
|
|
|||||
состоит |
во |
взятии |
наудачу |
трех |
|
|
|
|
|
|
|
|
|
|
|
|||
отрезков, длины которых x, y, z. Мы его |
|
|
|
|
|
|
|
|
|
|
|
|||||||
отождествим |
с |
экспериментом, |
|
|
|
|
|
|
|
|
|
|
|
|||||
состоящим во взятии точки из куба G. Из |
|
|
|
|
|
|
|
|
l |
x |
||||||||
этих трех |
отрезков можно построить |
l |
|
|
|
|
|
|
|
|
|
|
||||||
треугольник тогда и только тогда, когда |
|
|
|
|
|
|
|
|
|
|
||||||||
y |
|
|
|
|
|
|
|
|
|
|
||||||||
выполняются условия: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Рис.6 |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x + y > z,x + z > y,y + z > x.
Эти неравенства определяют область D. Область D получается отбрасыванием от куба трех
тетраэдров, отсекаемых плоскостями x + y = z , x + z = y , y + z = x |
(см. рис.6). Объем каждого |
|||||||
|
l 3 |
, следовательно, mesD = l 3 −3 l 3 |
= l 3 |
|
|
l 3 |
|
= 1 . |
тетраэдра равен |
и искомая вероятность p = |
2 |
|
|||||
6 |
l 3 |
|
||||||
|
6 |
2 |
|
|
2 |
|||
Литература.
1)Гнеденко Б. В. Курс теории вероятностей.
2)Ширяев А. Н. Вероятность.
3)Свешников А. А. и др. Сборник задач по теории вероятностей, математической статистике и теории случайных функций.
