
- •Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл
- •Предисловие
- •Понятие определенного интеграла. Вычисление определенных интегралов
- •1. Понятие определенного интеграла
- •2. Условия интегрируемости функций
- •4. Свойства определенного интеграла
- •5. Вычисление определенного интеграла
- •1. Непосредственное интегрирование.
- •2. Интегрирование по частям определенного интеграла
- •3. Замена переменной в определенном интеграле
- •Решение задач I типового варианта
- •6. Вычисление несобственных интегралов
- •Решение задач II типового варианта
- •7. Приложение определенных интегралов к задачам геометрии
- •1. Вычисление площадей плоских фигур
- •2. Вычисление объемов тел вращения
- •3. Вычисление длин плоских кривых при различных способах задания линий основные понятия и формулы
- •Решение задачи III типового варианта
- •Решение задачи IV типового варианта
- •Знания и умения, которыми должен владеть студент
- •1. Знания на уровне понятий, определений, описаний, формулировок
- •Содержание
- •Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию ГОУ ВПО

Государственное образовательное учреждение
высшего профессионального образования
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ГИДРОМЕТЕОРОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
В. Н. Веретенников
Учебно-методическое пособие для выполнения индивидуального задания определенный интеграл







Р Г Г М У
Санкт-Петербург
2007
Одобрено Научно-методическим советом РГГМУ
УДК 51
Веретенников В. Н. Учебно-методическое пособие для выполнения индивидуального задания. Определенный интеграл. – СПб.: Изд. РГГМУ. 2007. – 30 с.
Активизация познавательной деятельности студентов, выработка у них способности самостоятельно решать достаточно сложные проблемы может быть достигнута при такой организации учебного процесса, когда каждому студенту выдаются индивидуальные домашние задания (ИДЗ) с обязательным последующим контролем их выполнения и выставлением оценок.
Предлагаемое пособие адресовано преподавателям и студентам и предназначено для проведения практических занятий и самостоятельных (контрольных) работ в аудитории и выдачи ИДЗ.
© Веретенников В. Н.
© Российский государственный гидрометеорологический университет (РГГМУ), 2007.
Предисловие
"Математика" является не только мощным средством решения прикладных гидрометеорологических задач, но также и элементом общей культуры. Именно в рамках математического образования студент получает навыки творческого подхода к решению интеллектуальных проблем, точному пониманию средств возможностей решения проблем, знакомится с современными информационными технологиями.
Целью математического образования является:
Воспитание достаточно высокой математической культуры.
Привитие навыков современных видов математического мышления.
Привитие навыков использования математических методов и основ математического моделирования в практической деятельности.
Воспитание у студентов математической культуры включает в себя ясное понимание необходимости математической составляющей в общей подготовке студента. Он должен выработать представление о роли и месте математики в современной цивилизации и в мировой культуре, уметь логически мыслить, оперировать с абстрактными объектами и быть корректным в употреблении математических понятий и символов для выражения количественных и качественных отношений.
В пособии приведены основные теоретические сведения, отражающие базисные понятия по разделу "Определенный интеграл"; базисные методы решения основных задач; приведен перечень знаний, умений и навыков, которыми должен владеть студент; указана используемая литература.
Понятие определенного интеграла. Вычисление определенных интегралов
1. Понятие определенного интеграла
Определение 1.
Разбиением
![]() отрезка
отрезка
![]() ,
называется конечная система точек
,
называется конечная система точек
![]() этого отрезка такая, что
этого отрезка такая, что
![]() .
.
Отрезки
![]() называются отрезками
разбиения
.
называются отрезками
разбиения
.
Максимум
![]() из длин отрезков
из длин отрезков
![]() разбиения называется параметром
разбиения
.
разбиения называется параметром
разбиения
.
Определение 2.
Говорят, что имеется разбиение
![]() с отмеченными точками отрезка
с отмеченными точками отрезка
![]() ,
если имеется разбиение
отрезка
и в каждом из отрезков
,
если имеется разбиение
отрезка
и в каждом из отрезков
![]() разбиения
выбрано по точке
разбиения
выбрано по точке
![]() .
.
Набор
![]() обозначается одним символом
обозначается одним символом
![]() .
.
Пусть
функция
![]() определена на отрезке
,
где
определена на отрезке
,
где
![]() .
Если:
.
Если:
на отрезок нанести разбиение с отмеченными точками,
вычислить значения функции в отмеченных точках и
составить сумму
![]() ,
,
то она называется интегральной суммой функции на отрезке .
Геометрически
сумма
![]() представляет собой алгебраическую
сумму площадей прямоугольников, в
основании которых лежат частичные
отрезки
представляет собой алгебраическую
сумму площадей прямоугольников, в
основании которых лежат частичные
отрезки
![]() ,
а высоты равны
,
а высоты равны
![]() .
.
По-разному
деля отрезок
на
![]() частичных отрезков и по-разному выбирая
в них отмеченные точки, можно для всякой
заданной функции
и всякого заданного отрезка
составить бесчисленное множество
различных интегральных сумм. При этом
оказывается, что все эти различные
интегральные суммы при неограниченном
возрастании
и при стремлении к нулю параметра
разбиения, имеют один общий предел.
частичных отрезков и по-разному выбирая
в них отмеченные точки, можно для всякой
заданной функции
и всякого заданного отрезка
составить бесчисленное множество
различных интегральных сумм. При этом
оказывается, что все эти различные
интегральные суммы при неограниченном
возрастании
и при стремлении к нулю параметра
разбиения, имеют один общий предел.
Определение.
Число
![]() называется пределом интегральных сумм
называется пределом интегральных сумм
![]() функции
на отрезке
,
если для любого числа
функции
на отрезке
,
если для любого числа
![]() найдется число
найдется число
![]() такое, что для любого разбиения
отрезка
на части с длинами
такое, что для любого разбиения
отрезка
на части с длинами
![]() для всех
для всех
![]() (т. е.
(т. е.
![]() ),
неравенство
),
неравенство
![]() будет выполняться при любом выборе
точек
будет выполняться при любом выборе
точек
![]() .
.
Для обозначения предела интегральных сумм употребляется запись
![]() .
.
Число
![]() зависит от выбора числа
зависит от выбора числа
![]() ,
и поэтому иногда пишут
,
и поэтому иногда пишут
![]() .
.
Определение.
Если при любых разбиениях отрезка
на частичные отрезки
и при любом выборе точек
в них, интегральные суммы
![]()
![]() имеют один и тот же конечный предел
,
то этот предел называют определенным
интегралом в смысле Римана от функции
по отрезку
.
имеют один и тот же конечный предел
,
то этот предел называют определенным
интегралом в смысле Римана от функции
по отрезку
.
Обозначение:
![]() .
.
Итак, по определению
![]() .
.
Числа
![]() называются соответственно нижним
и верхним пределами интеграла;
называются соответственно нижним
и верхним пределами интеграла;
![]() называется переменной
интегрирования;
– подынтегральной
функцией,
называется переменной
интегрирования;
– подынтегральной
функцией,
![]() – подынтегральным
выражением.
– подынтегральным
выражением.
Так как определенный интеграл определен нами при условии, что , то дополним его определение следующими соглашениями: будем считать, что
если
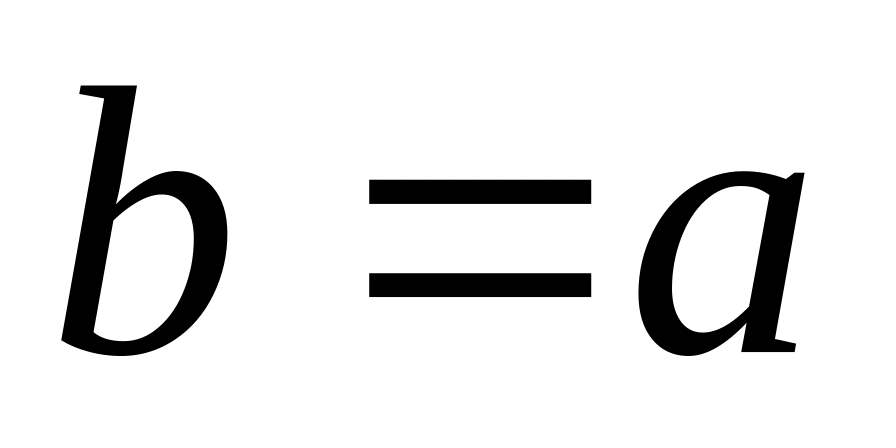 ,
то
,
то
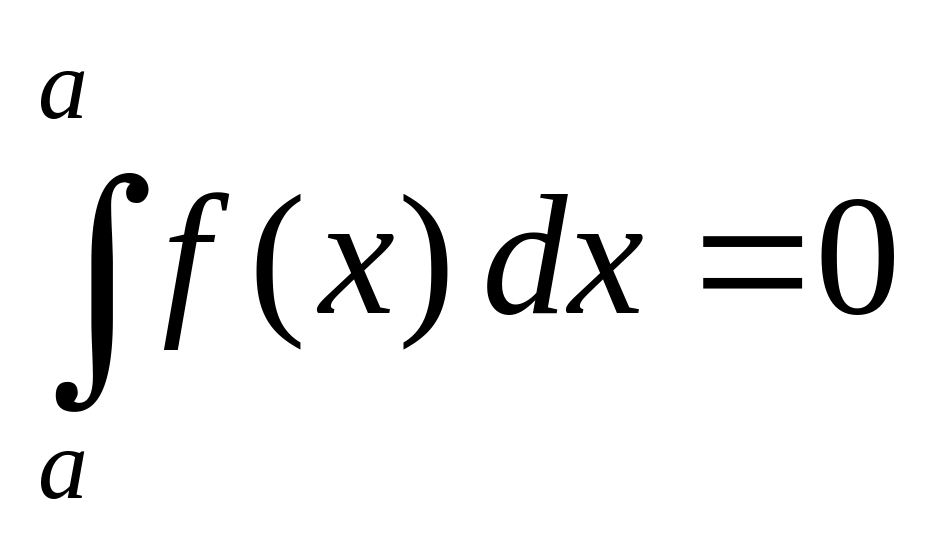 ;
;если
 ,
то
,
то
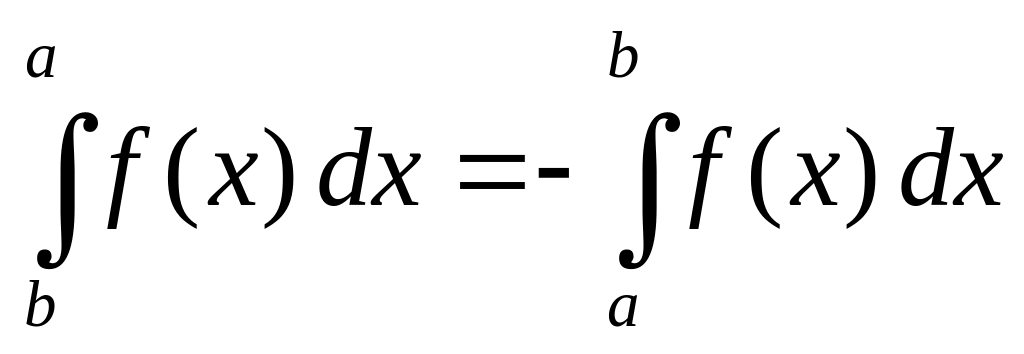 .
.
