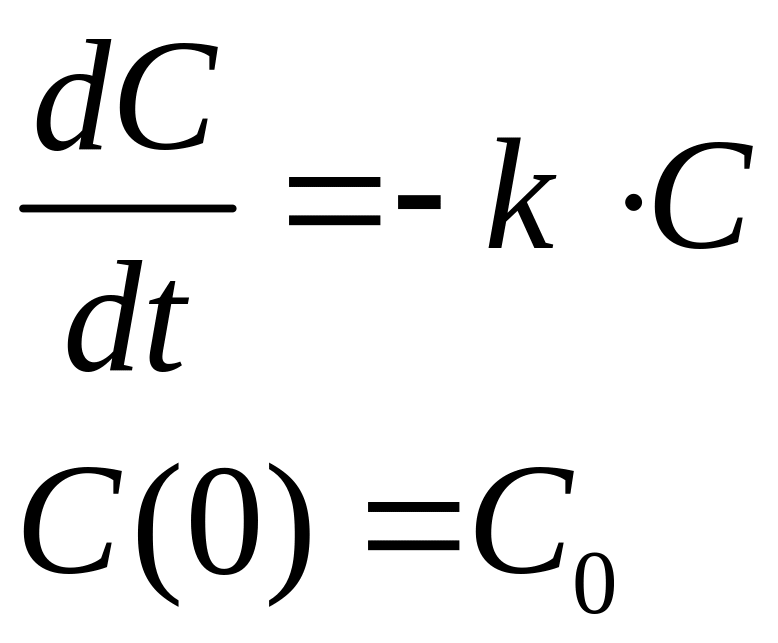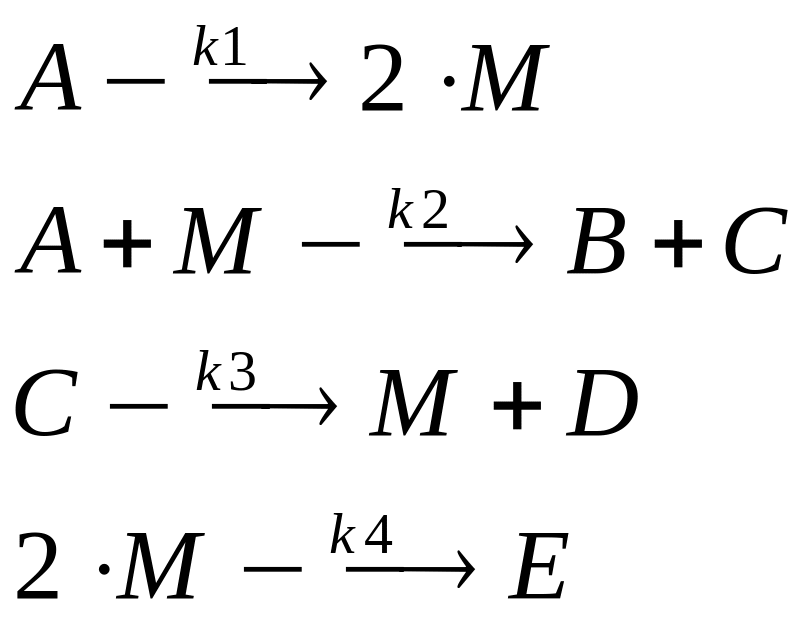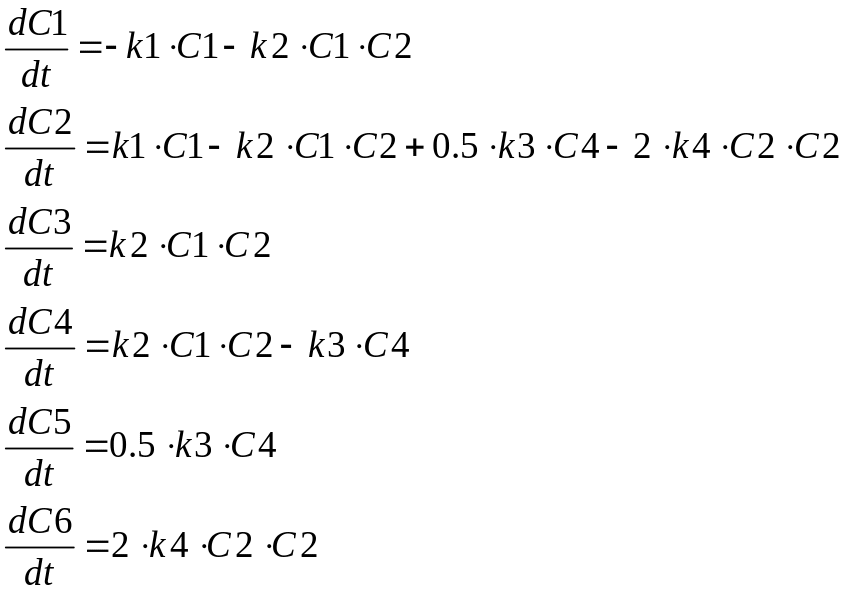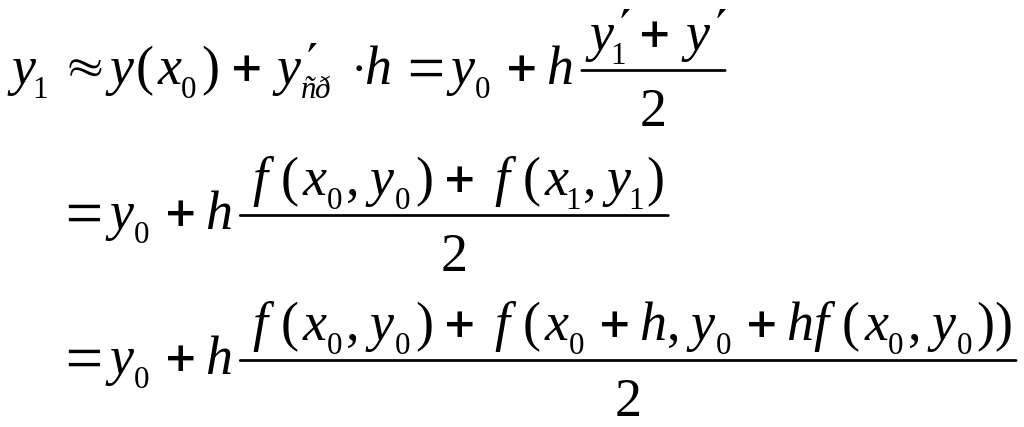Лекция. Численное решение задачи Коши для обыкновенных дифференциальных уравнений

Цель: Дать представление об основных идеях численного решения задачи Коши для обыкновенных дифференциальных уравнений и показать возможности MathCad для решения этой задачи.

Введение. Подавляющее большинство физических процессов описывается дифференциальными уравнениями. Простейшим примером может служить уравнение движения материальной точки:

(1)

При определенных начальных условиях:

(2)

Для химика дифференциальные уравнения — это, прежде всего, дифференциальные уравнения химической кинетики.

Для простейшей реакции разложения вещества скорость реакции пропорциональна первой степени концентрации (реакция первого порядка) и потому можно записать

(3)

где k называется константой скорости реакции, а — начальная концентрация.

Это уравнение в силу своей простоты легко решается (без привлечения численных методов):

(4)

Небольшое уточнение этой задачи приводит к гораздо более сложному уравнения.

Пусть порядок реакции будет равен n. Кроме того, рассмотрим реакцию с выделением тепла (тепловой эффект равен H). Если реактор помещен в термостат с температурой , то количество тепла, передаваемое от него к термостату, можно считать пропорциональным разности температуры T в реакторе и температуры . Если принять, что скорость выделения тепла пропорциональна скорости реакции, то для температуры получим дифференциальное уравнение

(5)

Зависимость константы скорости реакции от температуры обычно описывается уравнением Аррениуса, и следовательно для концентрации можно записать дифференциальное уравнение:

(6)

Для полученной системы уравнений (в которой концентрация C и температура T взаимосвязаны между собой) уже чрезвычайно трудно получить аналитическое решение, и приходится обращаться к численным методам.

Без учета температуры, типичная схема реакции может иметь, например, такой вид

(7)

Обозначая концентрации веществ A, M, B, C, D и E через С1, С2, C3, C4, C5 и С6, можно записать систему дифференциальных кинетических уравнений для этой схемы реакций в виде:

(8)

Обратите внимание, что суммарный баланс вещества должен быть равен нулю (в чем можно убедиться, сложив правые части уравнений). Эта систему уравнений должна решаться при определенных начальных условиях — начальных концентрациях.

Наличие нелинейностей в последней системе дифференциальных уравнений делает ее безнадежной с точки зрения получения аналитического решения.

Посмотрите, однако, что требуется набрать в MathCad, чтобы получить решение этой системы дифференциальных уравнений (рис1)..

На следующем рисунке приведены результаты расчет концентраций (их зависимости от времени) для всех веществ.

Обратите внимание на то, что результирующая концентрация продуктов (веществ B, D, E) равна в сумме концентрации исходного вещества A (0.4+0.4+0.2=1), что является дополнительной проверкой выполнения общего баланса вещества.

Как видите, запись системы дифференциальных уравнений в MathCad мало отличается от лычной математической записи на бумаге. Надо только эти уравнения и начальные условия заключить внутрь блока Given …..Odesolve.

Однако если щелкнуть правой кнопкой мыши по слову OdeSolve, то появится меню (рис.3), в котором вы можете выбрать метод решения дифференциальных уравнений. Для того, чтобы осознанно выполнять этот выбор для конкретной задачи, необходимо иметь общее представление об этих методах.

Целью данной лекции как раз и является изложение общих идей численных методов решения задачи Коши для обыкновенных дифференциальных уравнений.

Рисунок 1. Блок для решения системы дифференциальных уравнений ().

Рисунок 2. Результаты расчет системы уравнений. Зависимости концентраций веществ от времени.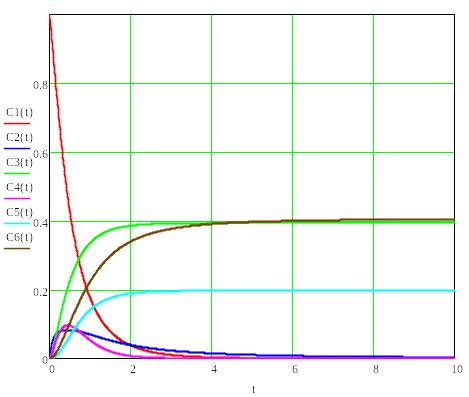

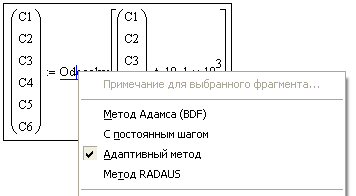
Рисунок. 3. Выпадающее меню для выбора метода решения дифференциальных уравнений.

Постановка задачи

Требуется численно решить задачу Коши (с начальными условиями) для системы обыкновенных дифференциальных уравнений:

(9)

Все последующее изложение будем вести для одного уравнения:

(10)

Все сказанное без труда (и практически без каких-либо изменений) переносится на случай нескольких уравнений.

Метод Эйлера

Итак, требуется найти решение задачи(10).

Решение дифференциального уравнения представляет собой семейство интегральных кривых, среди которых выбирается одна, проходящая через начальную точку ( ). На рисунке 4 условно изображена эта искомая кривая, соответствующая решению задачи (10).

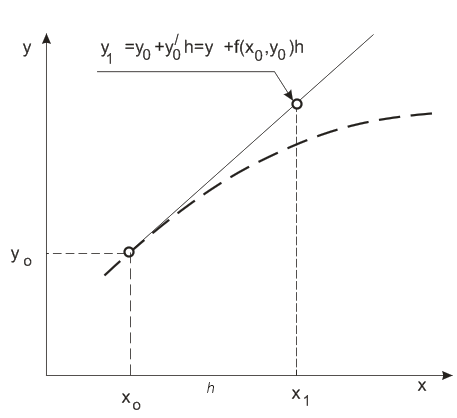
Кривая изображена пунктирной линией, поскольку она нам заранее неизвестна.

Основная идея численных методов решения задачи Коши содержится в методе Эйлера.

В окрестности точки ( ). Неизвестная функция может быть приближенно представлена формулой Тейлора:

,

что соответствует построению линейной функции, касательной к искомой функции y(x) в точке ( ).

Поэтому, если взять достаточно близко к и обозначить , то

Но величина также известна — ее можно вычислить из самого дифференциального уравнения . В итоге получим

(11)

Теперь решение (хотя и приближенно) известно в точке ( ). Поэтому можно повторить все предыдущие рассуждения и найти решение в следующей точке

И вообще

(12)

Можно повторять эти вычисления, получив последовательность значений , которая будет приближенно представлять решение данной задачи Коши.

Это и есть метод Эйлера.

Очевидно, чем меньше h (который называется шагом интегрирования), тем точнее будет решение.

Более того, можно заметить, что в формуле Тейлора ошибка e на каждом шаге имеет порядок . Если на всем отрезке интегрирования длиной L выполнить n шагов, то суммарная ошибка E будет суммой ошибок на всех отдельных шагах, то есть

То есть метод Эйлера имеет точность порядка O(h). Точную оценку получить затруднительно (она зависит от вида функции в правой части дифференциального уравнения), однако, полученная качественная информация оказывается очень полезной.

Уточнения метода Эйлера (методы второго порядка точности)

Чем обусловлена ошибка метода Эйлера?

Если бы производная от искомой функции не изменялась бы на отрезке , то касательная в точке ( ) точно бы совпадала с интегральной кривой, и метод Эйлера дал бы точное решение. Значит, ошибка связана с тем, что указанная производная на отрезке не постоянна. Поэтому естественно попытаться как-то учесть это изменение. Самым простым способом учесть такое изменение является попытка вычислить некоторое среднее значение этой производной на отрезке .

Это можно сделать несколькими способами.

а) вычислим среднее арифметическое значение производной в точках ( ) и ( ):

(13)

Эти рассуждения проиллюстрированы на рисунке 5.

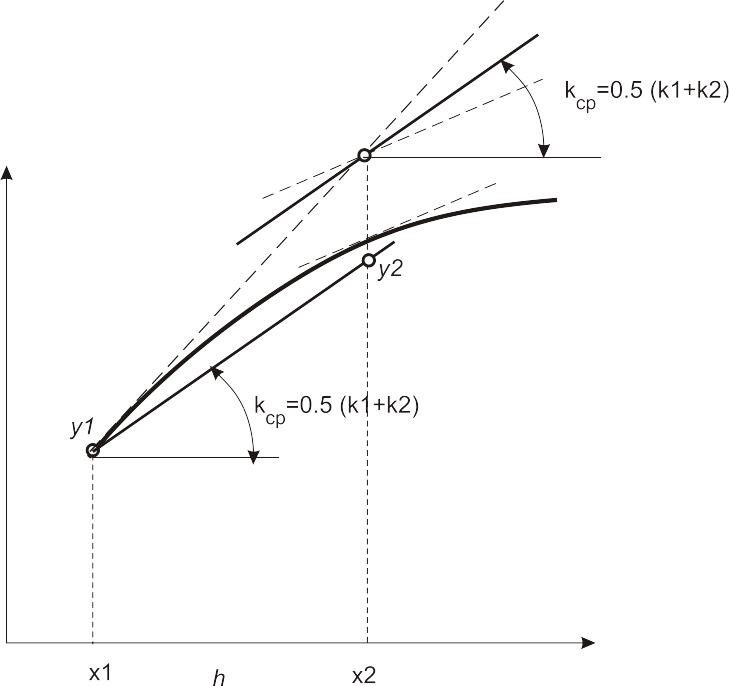
Рисунок 5

б) Можно также в качестве среднего значения производной на отрезке вычислить ее значение в промежуточной (например, средней) точке отрезка, то есть

(14)

Эти рассуждения проиллюстрированы на рисунке 6.

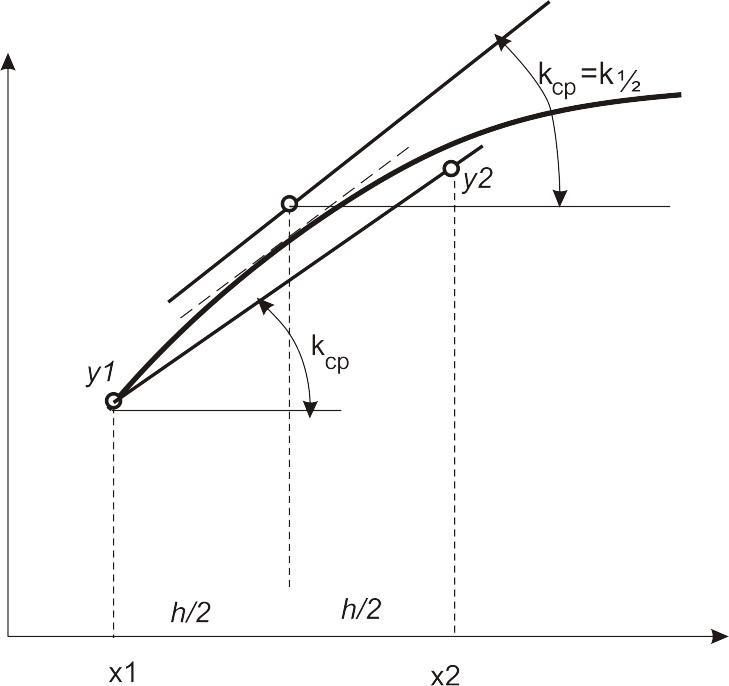
Рисунок 6.

Можно показать, что оба последних метода имеют точность порядка , то есть если уменьшить величину шага h в 10 раз, то погрешность решения уменьшится в 100 раз.

Метод Рунге-Кутта четвертого порядка

По аналогии с предыдущим можно получить и последующие уточнения метода Эйлера. Но поскольку геометрическая интерпретация в этих случаях затруднительна, а вывод занимает довольно много места, то просто приведем окончательную формулу метода четвертого порядка точности. Для того, чтобы ее можно было сравнивать с предыдущими методами 2-го порядка, перепишем последние, используя следующие обозначения:

(м-д Эйлера 1-го порядка)

(1-й м-д Эйлера 2-го порядка)

(2-й м-д Эйлера 2-го порядка)

Теперь можно легко поверить (опуская все выкладки), что метод 4-го порядка имеет вид

(15)

Все перечисленные методы образуют группу так называемых методов Рунге-Кутта (различного порядка точности). Можно построить методы Рунге-Кутта и более высокого порядка точности, но они используются редко.

Многоточечные методы (методы Адамса)

Все предыдущие методы определяют значение в последующей точке по значению в одной предыдущей точке . По этой причине их называют одношаговыми методами. При этом, если решение уже получено в нескольких предыдущих точка, то полученная в этих точках информация о решении не учитывается. Более того, основные затраты методов связаны с вычислением функции ( — правой части дифференциального уравнения) в новых промежуточных точках, в то время как в предыдущих точках такие вычисления были уже выполнены, и использование этих значений может уменьшить время вычислений.

Этот недостаток исправляется в так называемых многошаговых методах Адамса.

Чтобы получить представление об этих методах, запишем метод Адамса с двумя предыдущими точками (рисунок 7).

Построим его по аналогии с уточнением (б) метода Эйлера, но теперь возьмем в качестве исходной точку ( ), а среднее значение производной будем вычислять в точке ( ).

В итоге получим

(16)

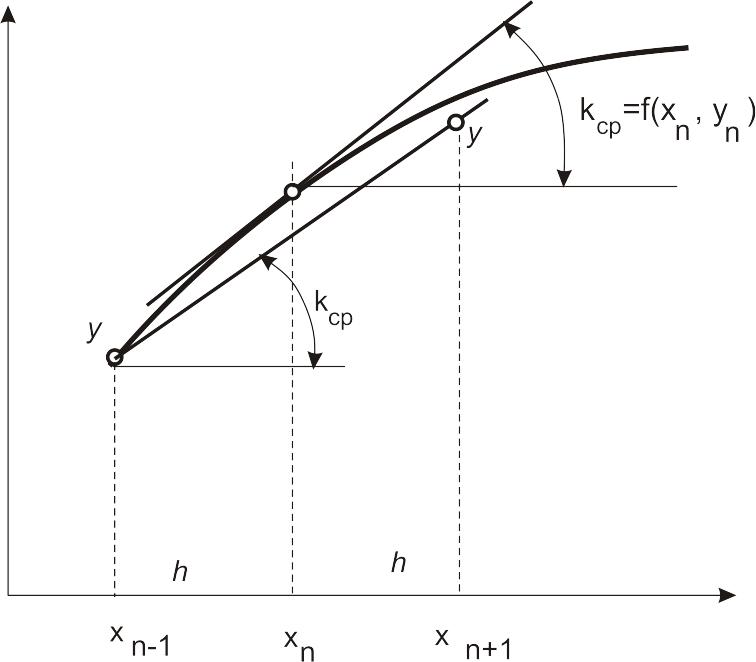
Рисунок 7. Простейший многошаговый метод Адамса.

Уточнения одношаговых методов Рунге-Кутта связаны с добавлением внутренних точек на отрезке . Точно также уточнения многошаговых методов связаны с добавлением нескольких предыдущих точек. Из-за громоздкости вычислений здесь эти формулы не приводятся (их можно н6айти, например, в книге Хемминга [].