
Конечные разности
х |
у |
|
|
|
|
|
_ |
_ _ |
_ _ _ |
В заключении отметим, что существует один и только один интерполяционный многочлен при заданном наборе улов интерполяции. Формулы Лагранжа, Ньютона порождают один и тот же многочлен, при условии, что вычисления проводятся точно. Разница лишь алгоритме их построения. Правда интерполяционный многочлен Лагранжа не содержит явных выражений для коэффициентов.
Выбор способа интерполяции (локальная или глобальная) определяется различными соображениями: точностью, временем вычислений, погрешностями округления.
В некоторых случаях более предпочтительной может оказаться локальная интерполяция, в то время как построение единого многочлена высокой степени (глобальная интерполяция) не приводит к успеху, т.е. повышение точности интерполяции напрямую не связано с повышением степени интерполяционного многочлена. Доказано (математик Рунге в 1901г.) что повышение точности интерполирования целесообразно производить за счет уменьшения шага интерполирования и специального расположения узлов интерполирования.
Метод наименьших квадратов
Один из видов точечной среднеквадратичной аппроксимации с помощью многочлена (2.2)
![]() ,
,
при этом
![]() ,
случай m=n
, соответствует
интерполяции глобальной как правило
m=1,2,3,
что можно сказать соответствует локальной
интерполяции. Однако это не так при
интерполировании основным условием
является прохождение графика
интерполяционного многочлена через
данные значения функции в узлах
интерполяции. При среднеквадратичном
приближении график интерполяционного
многочлена проходит близко от таблично
заданных значений функции.
,
случай m=n
, соответствует
интерполяции глобальной как правило
m=1,2,3,
что можно сказать соответствует локальной
интерполяции. Однако это не так при
интерполировании основным условием
является прохождение графика
интерполяционного многочлена через
данные значения функции в узлах
интерполяции. При среднеквадратичном
приближении график интерполяционного
многочлена проходит близко от таблично
заданных значений функции.
Мерой отклонения
многочлена
![]() от заданной функции
на множестве точек
от заданной функции
на множестве точек
![]()
![]() при Среднеквадратичном приближении
является величина
при Среднеквадратичном приближении
является величина
![]()
Для метода наименьших
квадратов значение S
должно быть минимальным. Это требование
позволит нам определить коэффициенты
![]() аппроксимирующего многочлена
.
аппроксимирующего многочлена
.
![]()
Так как в этой
формуле параметры
![]() выступают
в роли независимых переменных функции
S,
то ее минимум найдем, приравнивая нулю
частные производимые по этим переменным
выступают
в роли независимых переменных функции
S,
то ее минимум найдем, приравнивая нулю
частные производимые по этим переменным
![]()
Полученные соотношения представляют систему из m+1 уравнений для определения
![]()
![]()
![]()
Преобразуя, имеем
![]()
![]()
…
![]()
В компактной форме
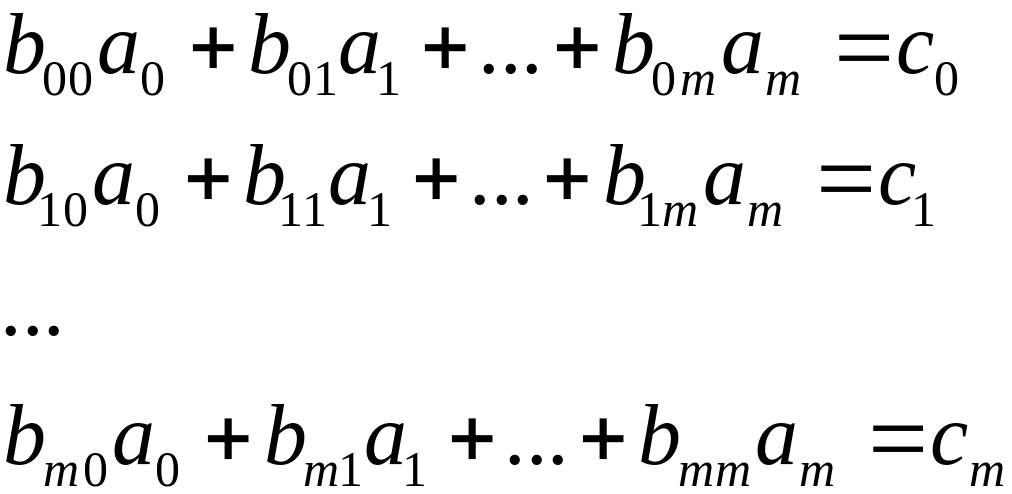
![]()
![]()
![]()
Система и m+1 линейного уравнения m+1 с неизвестным.
