
Исходные данные и формирование массива
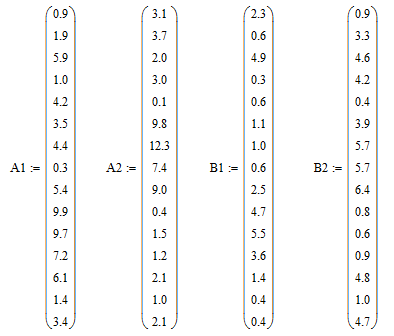
Исходный массив представляет собой данные, собранные в процессе работы судна типа pr 1348 в период 1988-1990 гг. Обработке и анализу в массиве данных подвергаются первый и четвёртый столбцы.
Данный массив представляет собой данные о среднесуточном вылове рыбы одним типом судна и среднее количество судов на промысле;
Для удобства исходная матрица была разбита на два массива:
А – среднесуточный вылов рыбы одним типом судна ;
В - среднее количество судов на промысле;
Эти массивы представлены матрицами, состоящими из 30 строк и 1 столбца.
Для удобства массивы были разбиты на две части. Объединим их.
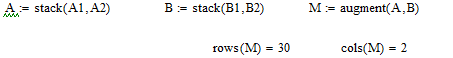
Вычисление статистических характеристик массива Вычисляем выборочную среднюю:
Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.
Задаем n и i :
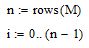
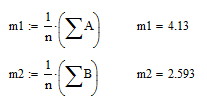
С помощью встроенных функций Mathcad:
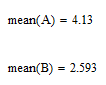
Вычисляем дисперсию
Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения выборочной средней.
Дисперсия является оценкой одноименного показателя теории вероятности. Сопоставление линейных или среднеквадратических отклонений по признакам совокупности дает возможность определить статистическую однородность совокупности: чем меньше размер, тем совокупность более однородна.
Находим дисперсию по формуле:

Найдем
дисперсию с помощью оператора var
и Var
:

Результаты вычисление совпадают, ошибки нет
Вычислим среднее квадратическое отклонение с помощью математических формул и встроенных функций Mathcad

Найдем медиану с помощью оператора median
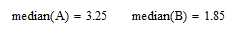
Найдем асимметрию по формуле. С помощью Mathcad
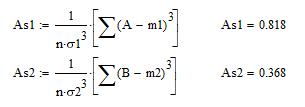
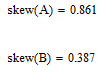
Для А асимметрия > 0 значит скошенна в право, и так как асимметрия < 1 скошенность считается средней.
Для B асимметрия > 0 значит скошенна в право, и так как асимметрия < 0,5 скошенность считается маленькой.
Найдем эксцесс по формуле. С помощью Mathcad
.
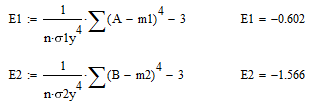
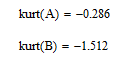
Так как эксцесс < 0 то вершина кривой распределения ниже (плосковершинность) , чем кривая Гауса.
Построение гистограммы плотности распределения. Графическое сравнение с нормальным распределением
Располагаем массив данных в порядке возрастания
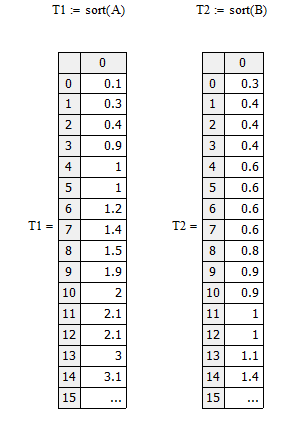
Находим максимальные и минимальные значения массива

Находим число интервалов по формуле Стерджеса
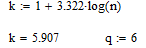
Находим шаг интервалов
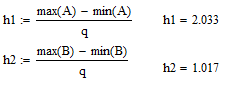
Распределяем варианты по интервалам
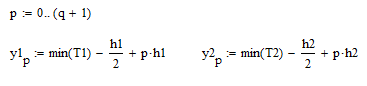
Находим частоты на каждом из интервалов
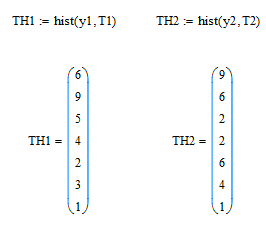
Сравниваем гистограммы с нормальным распределением
Запишем функцию плотности
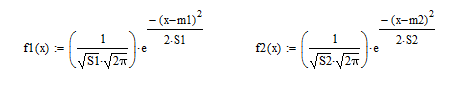
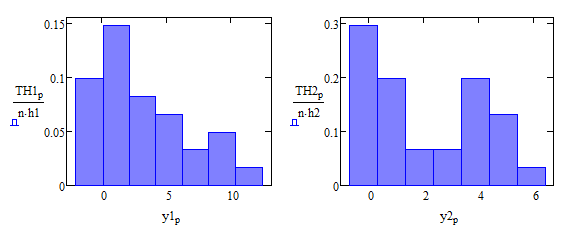
Гистограмма - количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.
Таким образом, гистограмма представляет собой графическое изображение зависимости частоты попадания элементов выборки от соответствующего интервала группировки.
Строим гистограммы плотности распределения
Сравниваем гистограммы с нормальным распределением
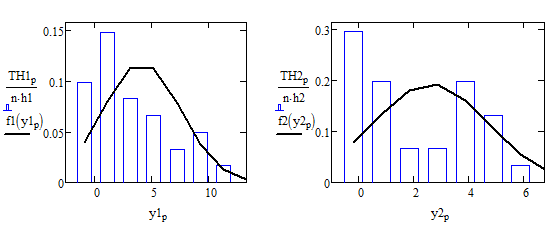
Сравнив гистограммы с нормальным распределением, можно делать вывод, что гистограмма плотности распределения отлично от нормального распределения.
Построение доверительных интервалов для найденных статистических оценок
Для матожидания:
Найдем t как корень уравнения
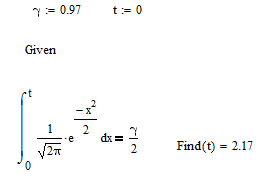
Чтобы найти t, можно использовать встроенную функцию
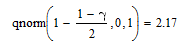
Найдем левый и правый края доверительного интервала
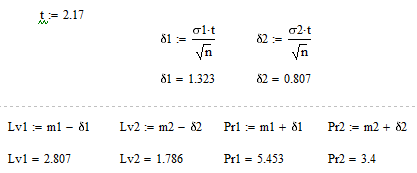
2.807<a<5.453
1.786<a<3.4
Для дисперсии
Вычислим квантили распределения Хи-квадрат
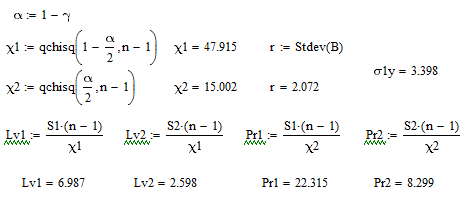
Среднее квадратическое отклонение
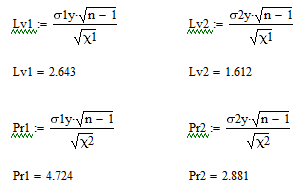
Проверка гипотезы о законе распределения
Преобразуем ряд в интервальный, так как число вариант велико

Зададим границы интервалов:
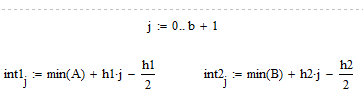
Получим интервальный ряд:

Получим интервальный вариационный
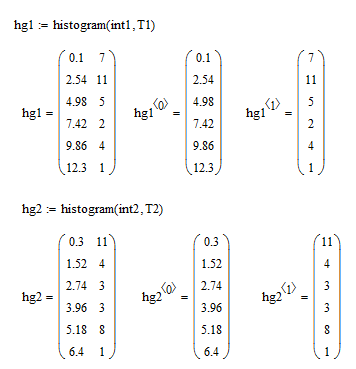
Убедимся, что сумма частот вариант равна объёму выборки
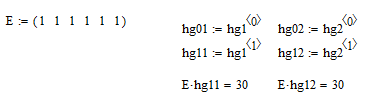
Находим числовые характеристики вариационного ряда: xv - выборочное среднее, sko – среднее квадратическое отклонение
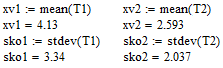
Задаем аргумент локальной функции Лапласа и находим все его значения
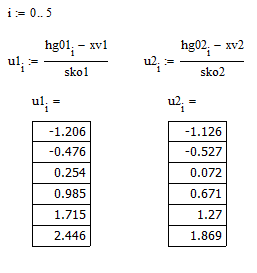
Определяем значения локальной функции Лапласа в найденных точках

Находим теоретические частоты
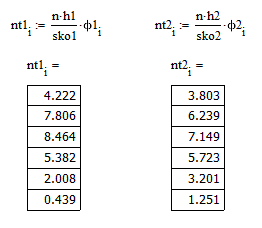
Убеждаемся, что сумма теоретических частот близка к объему выборки
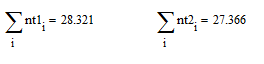
Объединяем соответствующие группы эмпирических частот
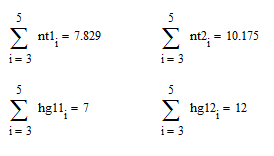
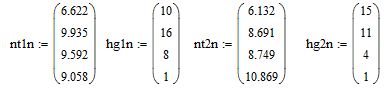
Вычисляем «хи-квадрат» наблюдаемое
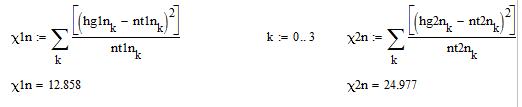
Применяя встроенные функции, находим «хи-квадрат» критическое

Так
как «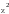 наблюдаемое»
больше «
критического»
для первого случая, то распределение
отлично от нормального.
наблюдаемое»
больше «
критического»
для первого случая, то распределение
отлично от нормального.
Так как « наблюдаемое» больше « критического» для второго случая, то распределение отлично от нормального.
Регрессионный анализ зависимости переменных
Корреляционное облако и выбор модели регрессии
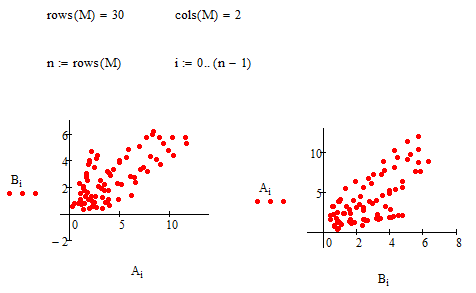
Уравнение Регрессии
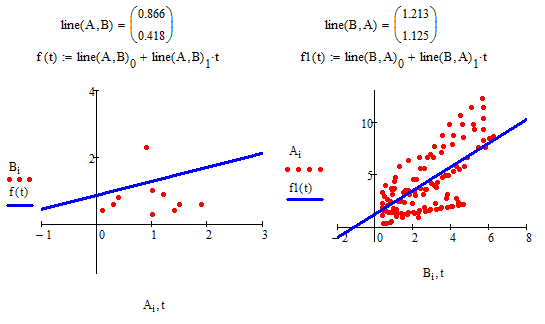
На графике характер расположения экспериментальных точек указывает, что связь между переменными близка к линейной.
Определяем среднюю ошибку аппроксимации
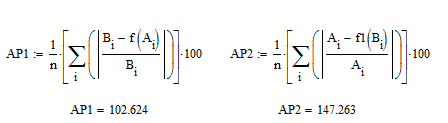
Так как ошибка аппроксимации велика, то полученную функциональную зависимость нельзя использовать для прогнозирования.
Определим коэффициент корреляции r и наблюдаемое значение критерия tN.
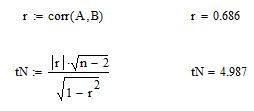
Определяем критическое значение критерия tK для двусторонней критической области
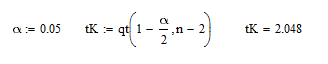
Так как tN > tK, то нулевую гипотезу не принимаем, следовательно, коэффициент корреляции значим, то есть, среднесуточный вылов рыбы одним типом судна оказывает существенное влияние на среднее количество судов на промысле.
Доверительный интервал для коэффициента коррреляции
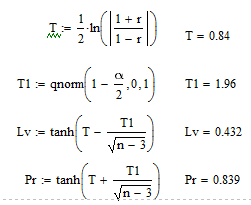
Следовательно, 0.432≤ r ≤ 0.839 – Доверительный интервал для коэффициента корреляции при уровне значимости 0,05.
Оценка статистической надёжности уравнения регрессии.
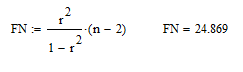
Критическое значение критерия
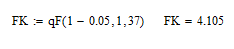
Так как FN > FK, то нулевую гипотезу не принимаем, следовательно, полученное уравнение регрессии является надёжным.
Коэффициент эластичности
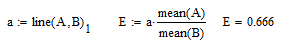
Следовательно, при увеличении среднесуточного вылова рыбы одним типом судна на 1% среднее количество судов на промысле увеличится на 0,6%.
Коэффициент детерминации
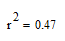
Следовательно, на 66,6% среднее количество судов на промысле зависит от – среднесуточный вылов рыбы одним типом судна, а на 33,4% от других факторов.
