11. Сумма подпространства. Теорема о размеренности суммы подпространств.

(“О” - значок изоморфности) Если любой вектор x О X может быть единственным образом представлен в виде x = x1 + x2, где x1 О X1 и x2 О X2 , то говорят, что пространство X разложено в прямую сумму подпространств X1 и X2 .

Прямая сумма обозначается X = X1 + X2 .

Любое линейное пространство может быть разложено в прямую сумму нескольких подпространств. В частности, разложение вектора по базису связано с разложением n–мерного пространства в прямую сумму n -одномерных подпространств

dimU +dimU┴=dimν; ортогональное дополнение единственно

Док-во:

ν >L₁;L₂ очевидно, что L₁∩L₂ подпространство ν;L₁+L₂ подпространство ν

Т. dim(L₁+L₂)= dimL₁+dimL₂ -dim (L₁∩L₂)

l₁l₂….l_m – базис L₁∩L₂

l₁l₂….l_m f₁f₂…f_k – базис L₁

l₁l₂….l_m g₁g₂….g_e –базис L₂

1)порождает систему L₁-L₂

L€ L₁+L₂=(α₁l₁+ α_nl_n+β₁f₁+ β_nf_n)+

+( α₁ⁿl₁+…+α_mⁿl_m+g₁g₂+...+g_eg_e+1)

2)l₁,l₂,….,l_m, f₁f₂…f_k, g₁…g_e- линейно независима

(*) λ₁l₁+…+ λ_ml_m+μ₁f₁+..+μ_kf_k+ν₁g₁+…+ ν_eg_e=(ноль с чертой сверху)

L₁€ λ₁l₁+…+ λ_ml_m+μ₁f₁+..+μ_kf_k=-ν₁g₁-…- ν_eg_e € L₂ L₁∩L₂

λ₁l₁+…+ λ_ml_m +of₁+…+f_k (???)

(**) μ₁₌ μ₂₌μ_k

из соотношения (*) получается линейная комбинация векторов базиса пространства L₂.

Из (*) и (**) имеем λ₁=…= λ_m= ν₁=…=ν_e=0

m + k + e = (m + k)+(e+m)-m

dim(L₁+L₂)=dimL₁+dimL₂-dim(L₁∩L₂);

m + k + e = dim(L₁+L₂), (m + k)= dimL₁ , (e+m)= dimL₂

12. Задача об определении линейной независимости системы векторов. Однородные и неоднородные системы линейных уравнений. Геометрическая интерпретация множества корней однородной системы. Матричная запись системы линейных уравнений.

Матричный метод решения систем линейных уравнений.

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Метод удобен для решения систем невысокого порядка.

Метод основан на применении свойств умножения матриц.

Пусть дана система уравнений:

Составим матрицы: A = ;

B = ; X = .

Систему уравнений можно записать: AX = B.

Сделаем следующее преобразование: A^-1AX = A^-1B,

т.к. А^-1А = Е, то ЕХ = А^-1В

Х = А^-1В

13. Эквивалентные системы, элементарные преобразования уравнений. Метод Гаусса решения системы линейных уравнений.

Две системы, множества решений которых совпадают, называются эквивалентными или равносильными (совпадение множеств решений означает, что каждое решение первой системы является решением второй системы, и каждое решение второй системы является решением первой). Системы, полученные в результате перестановки уравнений, умножения уравнения на любое число, отличное от 0; прибавления одного уравнения, умноженного на любое число, к другому уравнению эквивалентны.

Элементарные преобразования: перестановка строк; умножение всех элементов строки на любое число, отличное от нуля; прибавление элементов одной строки, умноженных на одно и то же число, к соответствующим элементам другой строки. Матрицы, полученные одна из другой с помощью элементарных преобразований строк, называются эквивалентными.

Рассмотрим квадратную систему: 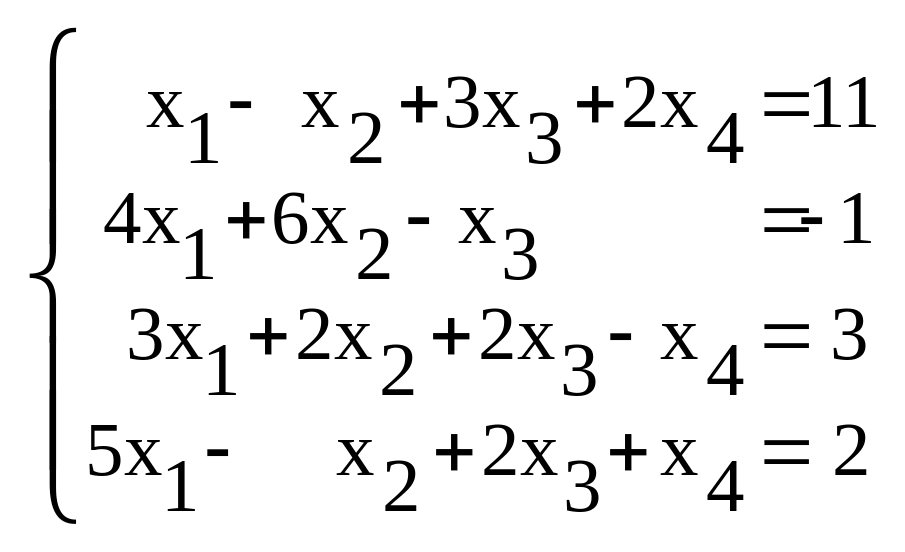(1)

У этой системы коэффициент a₁₁ отличен от нуля. Если бы это условие не выполнялось, то чтобы его получить, нужно было бы переставить местами уравнения, поставив первым то уравнение, у которого коэффициент при x₁ не равен нулю. Проведем следующие преобразования системы:1) поскольку a₁₁ 0, первое уравнение оставим без изменений;

2) вместо второго уравнения запишем уравнение, получающееся, если из второго уравнения вычесть первое, умноженное на 4;

3) вместо третьего уравнения запишем разность третьего и первого, умноженного на 3;4) вместо четвертого уравнения запишем разность четвертого и первого, умноженного на 5.Полученная новая система эквивалентна исходной и имеет во всех уравнениях, кроме первого, нулевые коэффициенты при x₁ (это и являлось целью преобразований 1 – 4):

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

Разделим обе части 1–го уравнения на a₁₁  0, затем:

1) умножим на а₂₁ и вычтем из второго уравнения

2) умножим на а₃₁ и вычтем из третьего уравнения

и т.д.

Получим:

, где d_1j = a_1j/a₁₁, j = 2, 3, …, n+1.

d_ij = a_ij – a_i1d_1j i = 2, 3, … , n; j = 2, 3, … , n+1.

Далее повторяем эти же действия для второго уравнения системы, потом – для третьего и т.д.

14. Общее решение однородной системы и общее решение неоднородной системы. Векторная запись корня системы, базис пространства корней однородной системы. Связь множества корней однородной и неоднородной систем.

Однородная система уравнений свободные члены которой = 0, наз-ся однородной. Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной. Основное утверждение относительно решений однородных систем содержится в теореме о структуре общего решения однородной системы: Если ранг r матрицы однородной системы линейных уравнений мерньше числа неизвестных n, то общее решение системы можно записать в виде

где — произвольные константы, а — фундаментальная система решений.Для общего решения линейной неоднородной системы справедлива теорема: Теорема. Если ранг r матрицы неоднородной системы линейных уравнений мерньше числа неизвестных n, то общее решение системы можно записать в виде

где — произвольные константы, а — фундаментальная система решений однородной системы, — некоторое (частное) решение неоднородной системы.

Заметим, что общее решение неоднородной системы линейных алгебраических уравнений равно сумме общего решения приведенной однородной системы и любого частного решения неоднородной системы. Заметим также, что неоднородная система линейных алгебраических уравнений имеет единственное решение тогда и только тогда, когда приведенная однородная система тривиально совместна, т.е. когда ранг матрицы системы равен числу неизвестных (r=n)., Необходимым и достаточным условием единственности решения неоднородной системы в случае m=n (число неизвестных совпадает с числом уравнений) является оличие от нуля определителя матрицы (условие detA≠0).