6. Точечная оценка дисперсии, ее смещенность. Исправленная выборочная дисперсия.

Точечной называют оценку, которая определяется одним числом из результатов выборки.

Пусть дана выборка: х₁, х₂, …х_{n .} Будем рассматривать выборочные значения как реализации случ. величин Х₁, Х₂, …Х_n , одинаково распределенных по закону распределения генеральной совокупности, т. е. случайной величины Х. Это означает, что они имеют одно и то же математическое ожидание М_х и дисперсию σ_х².

d_в = ^{2 (скобка в квадрате)}

Заменим конкретные реализации х_i на случ. величины Х_i, конкретные значения d_в - на случайное D_в и _в - на случайное , и преобразуем выражение: М(D_в) = М ( ((Х_i - М_х )-( - М_х ))²) = М ( (Х_i - М_х )²) - М ( ∑(Х_i - М_х ) ( - М_х ))+ М ( ( - М_х )²). Рассмотрим каждое слагаемое:

М ( (Х_i - М_х )²) = М(Х_i - М_х )² =

М ( ∑(Х_i - М_х ) ( - М_х )) = 2М( - М_х ) ( (Х_i - ))=2М( - М_х ) ( - М_х )= 2М( - М_х )²

М ( ( - М_х )²) = M( )=M( - М_х )²

Т. к. M( - М_х )² = D( )=D( )= , то М(D_в) = 2 + =(n-1) . Таким образом, математическое ожидание выборочной дисперсии не равно оцениваемой дисперсии генеральной совокупности σ_х², т. е. выборочная дисперсия является смещенной оценкой. Чтобы «исправить» выборочную дисперсию, ее нужно умножить на . Получим «исправленную» выборочную дисперсию: S² = D_в или для конкретной выборки: S² = d_{в .}

7. Понятие о точечных оценках параметров распределения. Метод моментов получения точечных оценок параметров распределения случайных величин.

Точечной называют оценку, которая определяется одним числом из результатов выборки.

Метод моментов точечной оценки неизвестных параметров заданного распределения состоит в приравнивании теоретических моментов соответствующим эмпирическим моментам того же порядка.

Если распределение определяется одним параметром, то для его отыскания приравнивают один теоретический момент одному эмпирическому моменту того же порядка – одно уравнение с одним неизвестным. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: v₁ = M_1. v₁ = M(Х), M₁ = _в , получаем: M(Х) = _в. Математическое ожидание является функцией от неизвестного параметра заданного распределения, поэтому, решив M(Х) = _в относительно неизвестного параметра, получим не сам параметр, а его точечную оценку, т. к. _в является реализацией случ. величины .

Если распределение определяется двумя параметрами, то приравнивают два теоретических момента двум соответствующим эмпирическим моментам того же порядка – два уравнения. Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка и центральный теоретический момент второго порядка центральному эмпирическому моменту второго порядка: v₁ = M₁ и μ₂ = m₂. Т. к. _. v₁ = M(Х), M₁ = _в , μ₂ = D(X), m₂ = D_в , имеем: M(Х) = _в , D(X) = D_в или D(X) = S². Левые части этих равенств являются функциями от неизвестных параметров, поэтому, решив эти два уравнения относительно неизвестных параметров, получим их точечные оценки.

Для вычисления _в и D_в (S²) надо располагать выборкой х₁, х₂, …х_{n .}

8. Метод моментов для построения оценок параметров равномерного распределения, нормального распределения, показательного распределения.

Равномерное распределение:

Допустим, имеется равномерное распределение следующего вида:

Находим оценку параметров a и b

Т.к. и , то (по методу моментов)

Т.к. распределение равномерное, то математическое ожидание:

Дисперсия Dx:

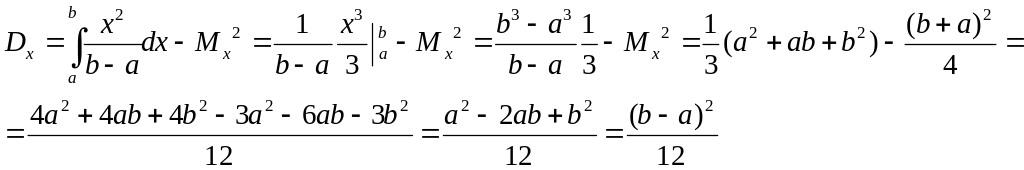
Получили, что (1)

(2)

Равенства (1) и (2) являются приближенными, т.к. правая часть их является случайной величиной. Таким образом, из уравнения (1) и (2) получается не точные значения а и b, а их оценка а* и b*: и

Тогда выразим один параметр через другой и получим: и подставим в уравнение (2):

Т.е. получили следующие оценки параметров a и b:

Показательное распределение:

Найти методом моментов по выборке x₁,x₂,..,x_n точечную оценку неизвестного параметра λ показательного распределения, плотность распределения которого f(x)= λ℮^-λx (x≥0)

Решение.

Приравняем начальный теоретический момент первого порядка начальному эмпирическому моменту первого порядка: υ₁=M₁ Учитывая, что υ₁=M(X), M₁=x⁻_в, получим M(X)= x⁻_в

Приняв во внимание, что математическое ожидание показательного распределения равно 1/ λ имеем, 1/ λ= x⁻_в отсюда λ=1/ x⁻_в

Итак, искомая точечная оценка параметра λ показательного распределения равна величине, обратной выборочной средней: λ=1/ x⁻_в

Нормальное распределение:

Найти методом моментов по выборке x₁,x₂,..,x_n точечные оценки неизвестных параметров a и σ нормального распределения

f(x)= (1/σ√2π)℮^(-(x-a)²/2σ²)

Решение.

Приравняем начальные теоретические и эмпирические моменты второго порядка, а также центральные и эмпирические моменты второго порядка:

υ₁= M₁, μ₂=m₂

Учитывая, что υ₁= M(X), μ₂=D(X), M₁= x⁻_в, m₂=D _в, получим M(X) = x⁻_в, D(X)= D _в

Приняв во внимание, что математическое ожидание нормального распределения равно параметру a, дисперсия σ² имеем:

a= x⁻_в, σ²= D _в

Итак, искомые точечные оценки параметров нормального распределения:

a= x⁻_в, σ=√ D _в