3. Реализация дифференциатора.

Проблема численного дифференцирования является достаточно старой и общей как в цифровых, так и в аналоговых регуляторах. Суть ее заключается в том, что производная вычисляется обычно как разность двух близких по величине значений функции, поэтому относительная погрешность производной всегда оказывается больше, чем относительная погрешность численного представления дифференцируемой функции.

В частности, если на вход дифференциатора поступает синусоидальный сигнал  , то на выходе получим  , т.е. с ростом частоты   увеличивается амплитуда сигнала на выходе дифференциатора. Иначе говоря, дифференциатор усиливает высокочастотные помехи, короткие выбросы и шум.

Рис. 5.66. Структурная реализация дифференциального члена ПИД-регулятора

Если помехи, усиленные дифференциатором, лежат за границей рабочих частот ПИД-регулятора, то их можно ослабить с помощью фильтра верхних частот. Структурная реализация дифференциатора с фильтром показана на рис. 5.66. Здесь  ,

т.е. передаточная функция полученного дифференциатора  может быть представлена в виде произведения передаточной функции идеального дифференциатора на передаточную функцию фильтра первого порядка:  , где коэффициент  задает граничную частоту фильтра и обычно выбирается равным 2...20 [Astrom].

Большее ослабление высокочастотных шумов можно получить с помощью отдельного фильтра, который включается последовательно с ПИД-регулятором. Обычно используют фильтр второго порядка [Astrom] с передаточной функцией  .

Постоянную времени фильтра обычно выбирают равной   , где  =2...20 [Astrom]. Граничную частоту фильтра желательно не выбирать ниже частоты  , т.к. это усложняет расчет параметров регулятора и запаса устойчивости.

Кроме шумов дифференцирования на характеристики ПИД-регулятора влияют шумы измерений. Через цепь обратной связи эти шумы поступают на вход системы и затем проявляются как дисперсия управляющей переменной  . Высокочастотные шумы вредны тем, что вызывают ускоренный износ трубопроводной арматуры и электродвигателей.

Поскольку объект управления обычно является низкочастотным фильтром, шумы измерений редко проникают по контуру регулирования на выход системы. Однако они увеличивают погрешность измерений   и снижают точность регулирования.

В ПИД регуляторах различают шум с низкочастотным спектром, вызванный внешними воздействиями на объект управления, и высокочастотный шум, связанный с электромагнитными наводками, помехами по шинам питания и земли, с дискретизацией измеряемого сигнала и другими причинами [Денисенко, Денисенко]. Низкочастотный шум моделируют как внешние возмущения ( ), высокочастотный - как шумы измерений ( ).

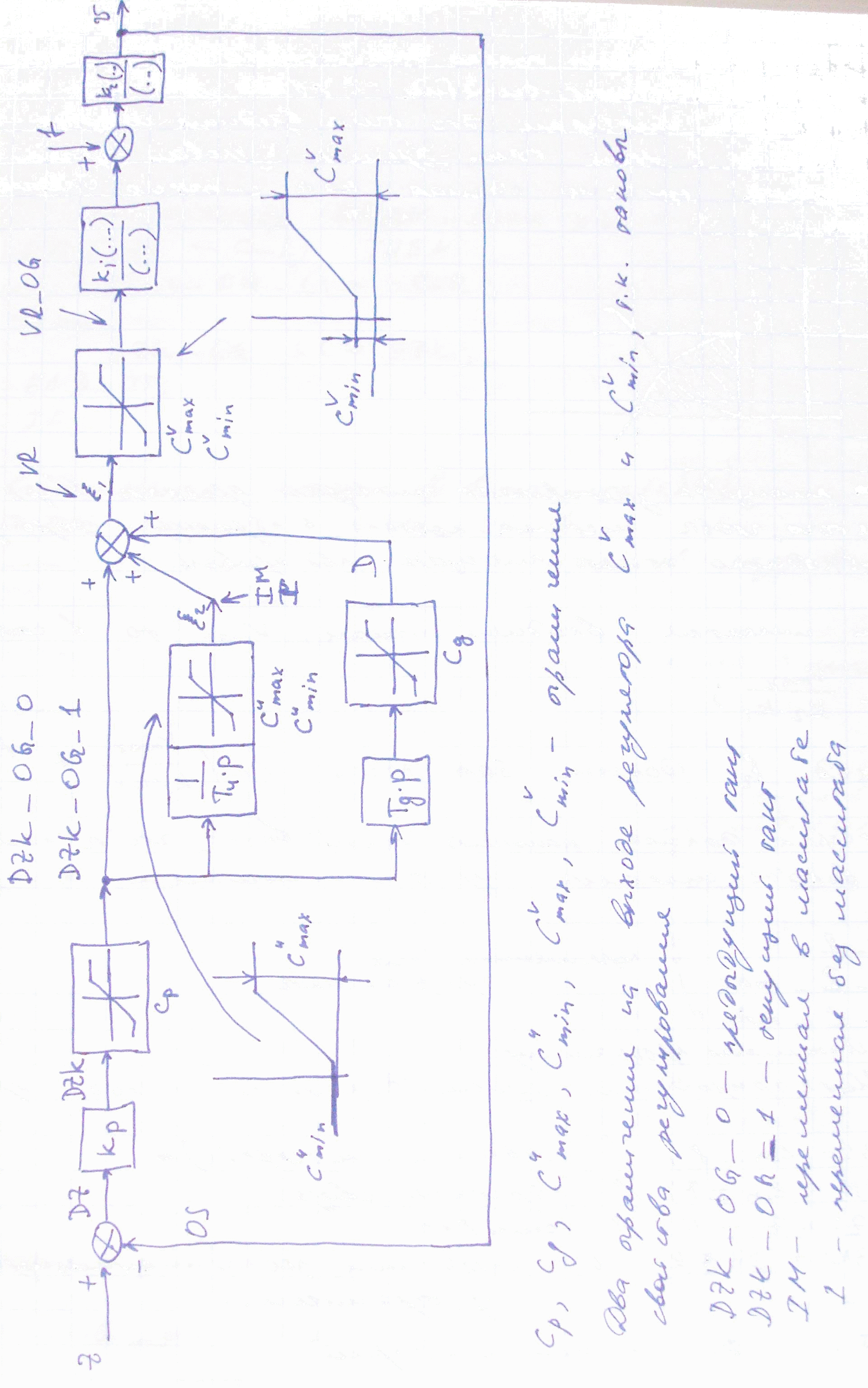
4. Алгоритм пид-регулятора.

ПИД-регулятор в непрерывной форме . У него есть пропорциональное, дифференциальное и интегральное звенья. Структурная непрерывная схема имеет вид:

Реальный регулятор обязательно имеет ограничения каждой из составляющих и суммарного сигнала в целом (в отличие от регулятора в ТАУ). В аналоговой технике ограничение выхода операционного усилителя достигается следующим способом:

Как только на стабилитронах повысилось напряжение до напряжения пробоя, то цепь со стабилитронами имеет низкое сопротивление. В цифровой технике ограничение сигнала достигается алгоритмически (оно всегда должно быть).

0 1 … 1 = +10 В

1 0 … 0 = -10 В

Каждый цифровой код имеет 12 разрядов. Если же происходит переполнение разрядной сетки, то напряжение меняется на противоположное. Причины ограничения:

1) не должно произойти переполнение разрядной сетки как по формату самого числа, так и по формату ЦАП.

2) С точки зрения теории и практики управления.

Нельзя ограничивать выход интеграла вот так:

Интеграл необходимо ограничивать прямо в процессе вычисления, на этапе: y_m:=y_m+x.

Если же сначала делать y:=y_m/T_DT, а потом его ограничивать, то будет ограничен только y на уровне С, а y_m нет. Правильно будет писать: y_m:=y_m+x; ограничение y_m на уровне С_m (C_m = C*T_DT).

Интеграл необходим только для исключения статической или динамической ошибки. Сточки зрения качества устойчивости интеграл – это очень вредная штука, плохой элемент и с этой точки зрения уровни ограничения интеграла нужно сделать как можно ближе к нулю. Если имеется выходной сигнал V_max, то в статике Выход должен быть равен , где 1,2 – запас. Интеграл должен накопить такой выход, чтобы получился на выходе системы нужный сигнал.

В программе это будет выглядеть следующим образом. Интегрирование будем делать по методу трапеций.

z:=lin_8; // задание (интерфейс)

OS:=lin_7; // обратная связь

DZ:=z-OS; // ошибка

DZK:=DZ*KR; // определение пропорциональной части без ограничения

…

Вычисление интеграла в масштабе:

IM:=IM+DZK_OG_1+DZK_OG_0;

Далее необходимо также ограничить IM на уровне CIM_max и CIM_min.

I:=IM_OG/(2*T_I/T_DT) – деление интеграла в масштабе на масштабный коэффициент (так как в Open PCS два деления подряд совершить невозможно, то необходимо ввести дополнительную переменную).

T2_DT:=2*T_I/T_DT;

Вычисление производной:

D:=(DZK_OG_1-DZK_OG_0)*(T_I/DT), где DT – это квант. Здесь также под T_D/DT необходимо завести переменную).

Подготовка следующей итерации:

DZK_OG_0:=DZK_OG_1;

Далее необходимо действовать по схеме, приведенной выше. Сначала ограничить величину D. Далее необходимо сложить все ограниченные величины. Итог суммирования опять ограничить. Затем полученный результат необходимо умножить на коэффициенты К1 и К2. В итоге получим нужный сигнал V_max.