Вопросы по дисциплине «Автоматизация технологических процессов и производств»

1. Цифровая реализация интегральных и дифференциальных звеньев. Методы целочисленного вычисления интегралов.

Особенностью реализации в цифровых системах интегрального звена является:

1) период ­­­­­­­­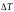– период квантования времени, с которым эти сигналы вычисляются (дискретность вычисления времени);

2) все вычисления должны быть целочисленные. Поскольку входные сигналы с АЦП это целые числа, выходные сигналы ЦАП – тоже целые числа, то делать вычисление внутри регулятора с плавающей точкой – это обманывать самого себя. Ошибка не может быть дробным числом в системе регулирования, оно только целое.

Основная задача: научиться целочисленному вычислению с заданной точностью этих самых интегралов. дальше ответа на вопрос 2

2. Методы целочисленного вычисления интегралов: метод прямоугольников, метод трапеций, метод Симпсона.

Метод целочисленного вычисления интегралов.

Пусть имеется интеграл: T – постоянная интегрирования, 1/p – это чистый интеграл во времени.

Входные сигналы сначала делятся на T, а потом интегрируются.

Методы вычисления интеграла отличаются друг от друга степенью полинома от времени входного сигнала при которой вычисление интеграла выполняется совершенно точно.

Для нулевой степени – метод прямоугольников, для первой степени – метод трапеций, для второй степени – метод Симпсона, для шестой степени – метод Уэдля.

Вычисление интеграла для полинома любой степени – метод Ньютона и Кортеса.

Метод прямоугольников

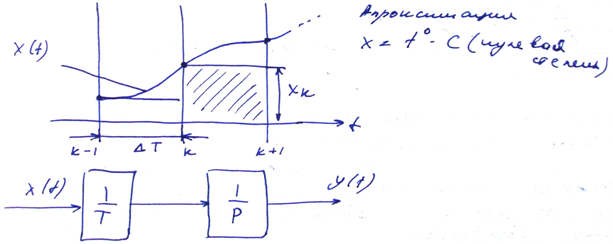
Входной сигнал апроксимируется полиномом нулевой степени. Входной сигнал на интервале считается постоянным. Формула для метода прямоугольников:

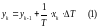
Масштабирование выходной переменой с учетом целочисленного алгоритма.

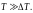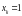Входные x и выходные y – это целые числа. Всегда выполняется условие Если то 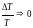(маленькое число), тогда

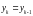
Для того чтобы не потерять точность и повысить чувствительность при целочисленном вычислении, необходимо ввести масштаб. Домножим уравнение (1) на коэффициент 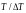. В результате получим: 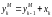, где 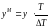– это масштаб выходного сигнала.

В программе это будет выглядеть так: y_m:=y_m+x; y:=y_m/T_DT; Комментарий: T_DT= .

Метод трапеций

Апроксимируется полиномом 1-ой степени: x = at + b (полином 1-ой степени).

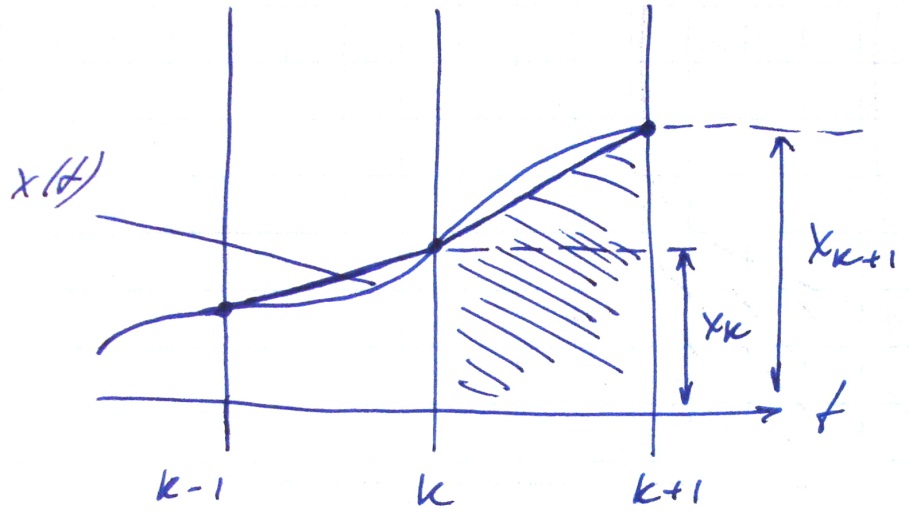
Таким образом, интеграл вычисляется по формуле: 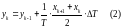– это формула для метода трапеций.

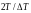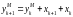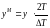С учетом целочисленности алгоритма необходимо ввести масштаб, т.е. необходимо домножить (2) на .С учетом этого интеграл имеет вид: , где . В программе это будет иметь вид: y_m:=y_m+x_1+x_0; y:=y_m/T2_DT; x_0:= x_1 (подготовка к следующей итерации, текущее значение x становится предыдущим). Комментарий: T2_DT= .

Метод Симпсона

Апроксимируется полиномом 2-ой степени: x = at² + bt+c (полином 2-ой степени).

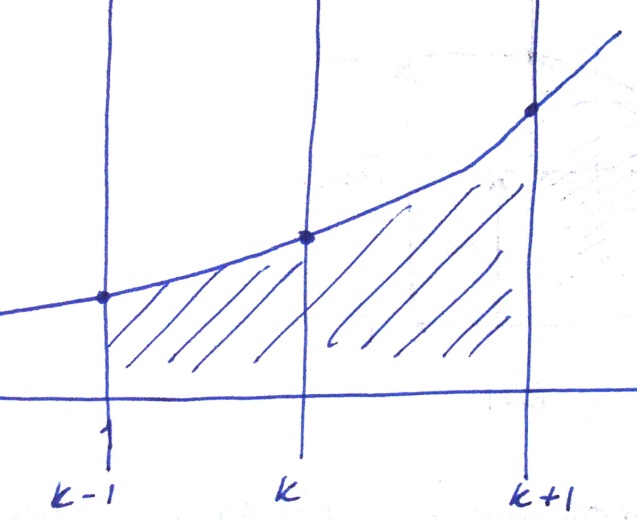
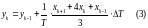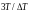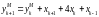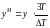Для определения параболы необходимо брать три точки. Формула Симпсона имеет следующий вид: . Площадь вычисляется за два такта, так как нельзя провести параболу по двум точкам. Масштаб имеет вид: . Тогда , где . В программе будет иметь вид: y_m:=y_m+ x_2+x_1+x_0; y:=y_m/T3_DT; x_0:= x_1; x_1:= x_2 (подготовка к следующей итерации). Комментарий: T3_DT= .