5.4. Представление данных в эвм.
В ЭВМ можно работать как с числами, так и с текстом. Это качественно различные виды данных, но принципы работы с ними довольно сходны.
Суть в том, что в каждом ЭВМ для представления информации используется некоторый фиксированный набор символов.
В IBM-совместимых типах ЭВМ используется 256 символов. Все символы, которые может напечатать компьютер закодированы в виде последовательности из 8 нолей и единиц, т.е. их можно рассматривать как восьмиразрядные двоичные числа от 00000000 до 11111111 или как двузначные шестнадцатеричные числа от 00 до FF; десятеричные от 0 до 255. Каждый символ (или код-число) занимает 1 байт памяти.
Все указанные символы делятся на две группы. Кодировка символов первой группы – символов с кодами – 0….127 выполнена по американскому стандарту ASCII и во всех IBM-совместимых ЭВМ неизменна. Эта группа включает заглавные буквы (коды 65-90), строчные буквы (97-122) латинского алфавита, цифры 0-9 (48-57), пробел (32), знаки препинания, математические и специальные управляющие символы. Вторая половина таблицы кодов (128-255) отведена для символов псевдографики и резерв для национальных алфавитов, который в каждой стране заполняется своими символами. В разных типах IBM-совместимых типах ЭВМ кодировка русских букв довольно часто различается (наиболее распространена альтернативная кодировка).
Из сказанного следует, что в ЭВМ и текстовая и числовая и прочая другая представляется в виде чисел, а значит, и обработка ее сводится к операциям над числами.
При вводе текста в ЭВМ код каждого символа текста записывается в отдельный байт запоминающего устройства.
Что касается числовых величин, то в ЭВМ каждая из них преобразуется к виду двоичного числа с фиксированной или плавающей точкой и записывается в ячейку определенного размера в зависимости от типа величины. Целые числа занимают 2 байта, т.е. 16 двоичных разрядов. Дробные числа (действительные) занимают 4 байта или 32 разряда. Если требуется записать большее число, то существует формат длинное целое (4 байта) и действительное с двойной точностью (8 байт).
Вывод. Латинские буквы в любой программной системе остаются неизменными, поэтому имена файлов и папок, темы писем в Интернете лучше писать латинскими буквами. Адреса Интернета и электронной почты состоят только из латинских букв. В переписке с заграницей тоже лучше использовать латинский алфавит. Однако, любой русский текст может быть прочитан с помощью программ перекодировщиков.
5.5. Логические основы эвм
ОПРЕДЕЛЕНИЕ 1. Логическими, или булевыми, переменными x1, x2,…, xn называются переменные, которые могут принимать только два значения: истина или ложь. В математической логике и в языках программирования понятие «истина» обозначается символом 1, понятие «ложь» – символом 0. В русской версии электронных таблиц EXCEL для логических переменных применяются значения «истина» и «ложь».
ОПРЕДЕЛЕНИЕ 2. Логической, или булевой, функцией от двоичных переменных называется такая функция, которая может принимать только два значения: 0 или 1.
Функция одного и двух двоичных переменных называются элементарными логическими функциями. Основными операциями являются инверсия (отрицание), конъюнкция и дизъюнкция.
Инверсия имеет
вид:
и определяется следующей таблицей
истинности.
x |
|
0 |
1 |
1 |
0 |
Конъюнкция
(логическое умножение) имеет вид:
и определяется следующей таблицей
истинности.
x |
y |
|
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Дизъюнкция
(логическое сложение) имеет вид:
и определяется следующей таблицей
истинности.
x |
y |
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
Операции инверсии, конъюнкции и дизъюнкции обладают следующими свойствами:
Закон двойного отрицания
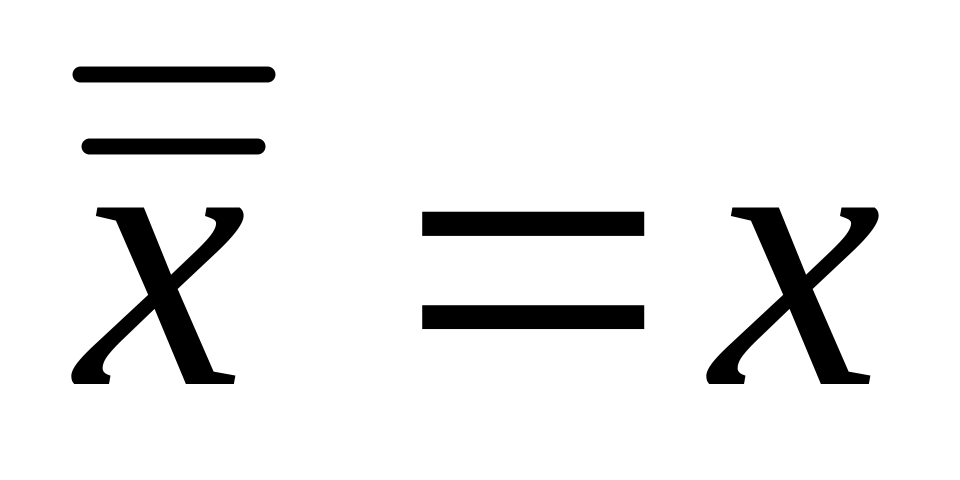;Коммутативность
;
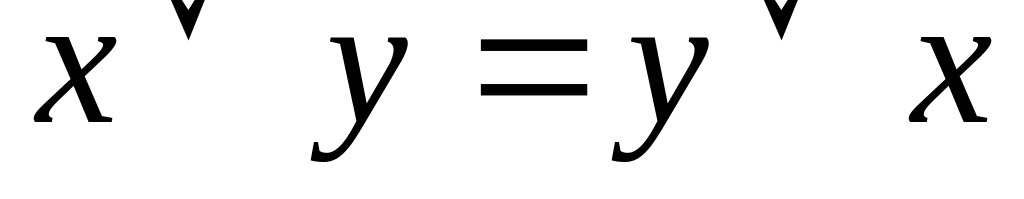;Ассоциативность
;
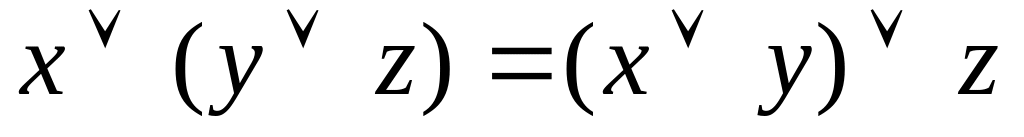;Дистрибутивность
;
;Правила де–Моргана
;
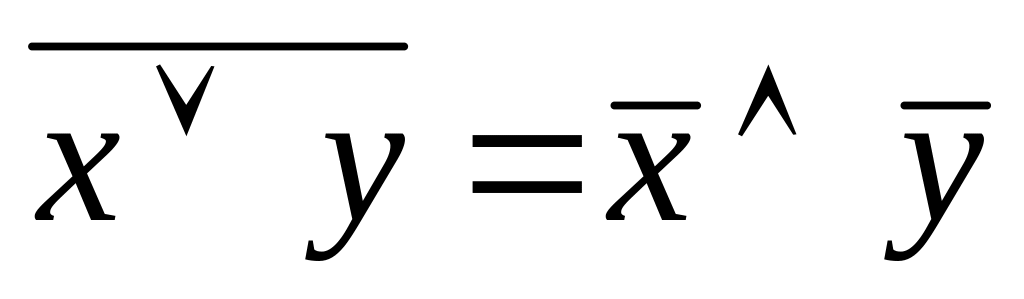;Законы поглощения
;
;Идемпотентность
.
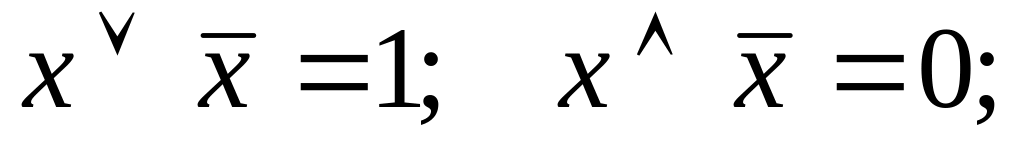
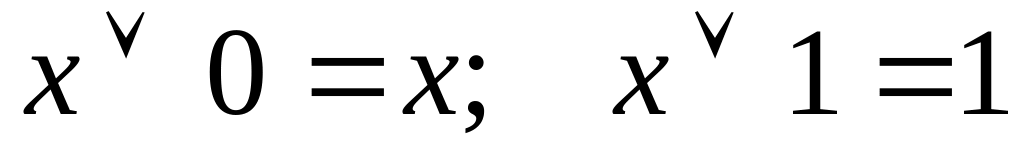Эти свойства операций называются также законами булевой алгебры.
Построим таблицу истинности для закона ассоциативности (x y) z = x (y z). Выписываем все переменные, которые входят в выражение. Затем от столбца к столбцу добавляем по одному действию так, чтобы в итогах получилась левая часть равенства, а затем делаем тоже самое делаем с правой частью. В первых трех столбцах выписываем все возможные значения переменных. Если переменных n, то строк - 2n. В нашем случае переменных 3, значит строк в таблице будет 8.
x |
y |
z |
x y |
(x y) z |
y z |
x (y z) |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
Как видно из таблицы левая часть выражения (5 столбец) и правая (7 столбец) при любых значениях переменных равны. Таблица истинности является одновременно проверкой и доказательством. Так как в таблице истинности перебираются все возможные значения переменных.
Более сложные логические выражения можно упростить, преобразовав их с помощью элементарных логических функций (используя законы булевой алгебры). Результат преобразования следует проверить по таблице истинности.
Построение функциональных логических схем по заданным функциям
При построении отдельных узлов компьютера довольно часто необходимо решить проблему построения функциональных логических схем по заданным функциям. Для этого достаточно условиться, что истинное высказывание соответствует тому, что цепь проводит ток, а ложное – цепь разорвана.
Логические операции конъюнкции, дизъюнкции, инверсии реализуются в ЭВМ с помощью следующих элементарных схем.
Конъюнкция – логический элемент «и»:
Этот элемент выполняет операцию логического умножения (конъюнкция): f = x1 x2 x3 …xn ; и имеет n входов и один выход.
Дизъюнкция – логический элемент «или»:
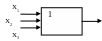
Этот элемент выполняет операцию логического сложения (дизъюнкция): f = x1 x2 x3 …xn ; и имеет n входов и один выход.
Инверсия – логический элемент «не»:
Этот элемент выполняет операцию логического отрицания (инверсии): f = ; и имеет один вход и один выход.
Сложные функциональные схемы можно конструировать из основных логических элементов, используя основные законы булевой алгебры