Государственный комитет Российской Федерации по высшему образованию

Санкт-Петербургский государственный электротехнический университет.

Кафедра ТОЭ.

Отчёт по лабораторной работе № 2.

«Исследование электростатического поля в однородных средах методом электромоделирования»

Выполнил: Комиссаров С.С. 9221

2001 г.

Цель работы:

Изучение полей двухпроводной линии и электронной линзы на моделях в электролитической ванне.

Основные теоретические положения.

В основе электромоделирования лежит математическая аналогия различного рода физических полей и поля электрического тока в проводящей среде. Рассмотрим поле в однородном диэлектрике при отсутствии свободных зарядов и поле постоянного тока в однородной проводящей среде.

Основные дифференциальные уравнения этих полей:

Электрические поля потенциальны и их потенциалы удовлетворяют уравнению Лапласа.

При совпадении краевых условий решение уравнения для обеих сред совпадают.

Электролитическая ванна представляет собой сосуд из диэлектрического материала, наполненный проводящей жидкостью, например водой. Электроды 1 установлены на дне ванны так, что их верхний край совпадает с уровнем воды. Электроды ограниченны сверху и снизу. Их удельная проводимость значительно больше удельной проводимости воды, поэтому ток, стекающий с электродов, зеркально отображается в границах раздела с сохранением знака и величины. Таким образом, поле отрезков электродов совпадает с плоскопараллельным полем бесконечно длинных электродов. Для исследования аксиально-симметричных полей необходимо установить электроды так, чтобы ось симметрии находилась на поверхности воды. Размер ванны должен быть достаточно большим, чтобы её стенки не влияли на исследуемое поле. На электроды подаётся переменное напряжение U₀ низкой частоты ( f=50-100Гц ). Перемещая зонд 2 по ванне можно определить положение эквипотенциальных линий.

Метод электролитической ванны – графический способ решения уравнения Лапласа. Картина поля – совокупность эквипотенциальных и векторных линий. Поверхности электродов, в обоих полях являются поверхностями равного потенциала. По полученным эквипотенциалям следует построить векторные линии электростатического поля так, чтобы поток во всех векторных трубках был одинаков .

Правила построения картины плоскопараллельного поля:

1. линии вектора непрерывны. Начинаются и заканчиваются на электродах (нет свободных зарядов)

2. Векторные и эквипотенциальные линии перпендикулярны.

3. Ячейки поля, полученные при пересечении эквипотенциальных и векторных линий, подобны. Это условие вытекает из требования постоянства потока 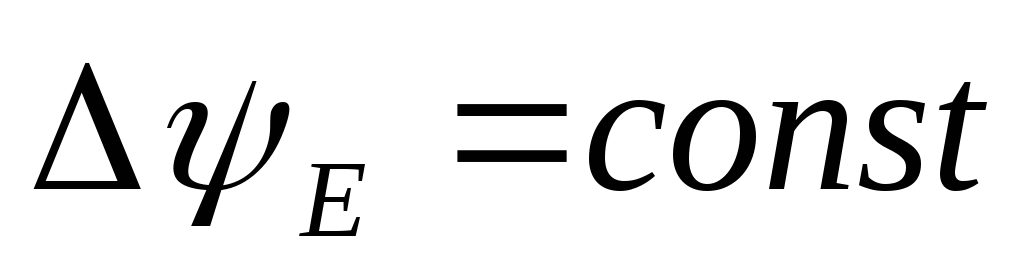и .

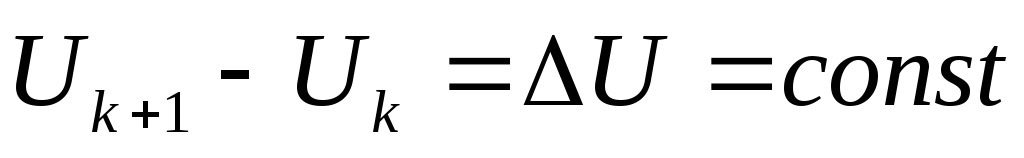Действительно, для k-той ячейки, полагая что поле в ней однородно, можно записать: . Поток в векторной трубке на единицу длины электродов . Так как , то b_k/a_k=const. Удобно принять b_k/a_k=1.

По построенной картине можно найти ряд важных характеристик поля.

Для определения поверхностной плотности зарядов на электродах используется граничное условие . Так как электростатическое поле в проводниках отсутствует, то .

Для определения ёмкости электродов на единицу длины полезно использовать представление о дискретной модели, построенной из параллельно и последовательно соединённых ёмкостей. Ёмкость k-той ячейки определяется как ёмкость плоского конденсатора . Ёмкости подобных ячеек одинаковы, поэтому можно записать , где m – число векторных трубок; n – число потенциальных перепадов.

Примером устройства с аксиально-симметричным полем является электронная линза. Она представляет собой два соосных цилиндра разных радиусов, к которым приложен напряжение. В поле линзы происходит фокусировка электронного потока. Преломляющими поверхностями являются поверхности равного потенциала.

При построении векторных линий поля электронной линзы первые два правила сохраняются. Однако требование постоянства потока в векторной трубке приводит к изменению условия подобия ячеек. Вычислим в сечении плоскостью перпендикулярной оси системы, и находящейся между электродов. , отсюда следует что: , где r_k – расстояние от оси до центра ячейки. Постоянная k вычисляется после построения трубки поля, которая образуется линией, совпадающей с осью симметрии, и первой векторной линией.

Расчёты.

Минимальная и максимальная плотности заряда могут быть оценены как , а нормальную составляющую вектора напряжённости можно найти из условия . Тогда для большего электрода имеем: , тогда соответственно

Ёмкость двухпроводной линии определится как

Выводы: