
Лабораторная работа №1
.DOC
ГОСКОМВУЗ РОССИЙСКОЙ ФЕДЕРАЦИИ
СПбГЭТУ
КАФЕДРА ТОЭ
Исследование электростатического поля в однородных средах методом электромоделирования.
Отчет по лабораторной работе №1
Студент гр.4221 Шамин Д. А.
Преподаватель
1996
Исследование электростатического поля в однородных средах методом электромоделирования.
Цель работы: изучение полей двухпроводной линии и электронной линзы на моделях в электролитической ванне.
Основные теоретические положения.
В основе электромоделирования лежит математическая аналогия различного рода физических полей и поля электрического тока в проводящей среде. В качестве примера рассмотрим электростатическое поле в однородном диэлектрике (e=const) при отсутствии свободных зарядов (r=0) и поле постоянного тока в однородной проводящей среде (g= const).
Основные дифференциальные уравнения этих полей:
rot E = 0 , div D = e div E = 0 ;
rot E = 0 , div J = g div E = 0.
Электрические поля потенциальны, причем потенциалы удовлетворяют уравнению Лапласа D U = 0.
При совпадении (подобии) краевых условий решение уравнения Лапласа для обеих сред совпадают, т.е. структуры полей, характеризуемые графическими картинами, одинаковы. Это позволяет исследовать электростатическое поле на его модели в проводящей среде, например, в электролитической ванне. Такой метод особенно плодотворен в тех случаях, когда краевые условия настолько сложны, что их нельзя сформулировать аналитически.
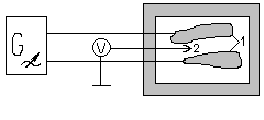
Электролитическая ванна представляет собой сосуд из изолирующего материала, наполненный проводящей жидкостью (водой) (рис 1). Электроды 1 устанавливаются на дне ванны так, что их верхний край совпадает с уровнем воды. Электроды ограничены с верху и снизу (воздух и дно ванны), их удельная проводимость значительно меньше удельной проводимости воды, поэтому ток, стекающий с электродов, зеркально отображается в границах раздела с сохранением знака и величены. Таким образом, поле отрезков электродов совпадает с плоскопараллельным полем бесконечно длинных электродов. Для исследования аксиально-симметричных полей необходимо установить электроды так, чтобы ось симметрии находилась на поверхности воды. Размеры ванны должны быть достаточно большими, чтобы стенки не влияли на исследуемое поле. На электроды подается переменное напряжение U0 низкой частоты (f = 50 - 100 Гц). Перемещая зонд 2 в ванне определить положение эквипотенциальных линий.
Рисунок 1
Правила построения картины плоскопараллельного поля:
-
линии вектора Е непрерывны, начинаются м заканчиваются на электродах ( в исследуемой области div E = 0);
-
векторные и эквипотенциальные линии перпендикулярны (Е = -grad U);
-
 Рисунок 2
Рисунок 2Рисунок 2
ячейки поля, полученные при пересечении эквипотенциальных и векторных линий, подобны. Это условие возникает из требований DyЕ = const и Uk+1 -Uk = DU =const, где DU - разность потенциалов между двумя соседними эквипотенциалями. Действительно, для k-й ячейки, пологая поле в ней однородным, можно записать Ek = DU/ak (рис.2). поток Е в векторной трубке на единицу длины электродов DyЕ = ЕkDSk = (DU/ak )/ bk 1 = const, где ak и bk - расстояния между эквипотенциалями и векторными линиями в k -ой ячейке. Так как DU = const, то bk/ak = const. Удобно принять bk/ak =1.
По построенной картине можно найти ряд важных характеристик поля.
Для определения поверхностной плотности зарядов s на электродах используется граничное условие Dn2 - Dn1 = s, где Dn2 и Dn1 - нормальные составляющие вектора смещения на границе раздела сред. Так как электростатическое поле в проводниках отсутствует, то s = Dn = eEn.
Для определения емкости электродов на единицу длины полезно использовать представление о дискретной модели, построенной из параллельно и последовательно включенных емкостей (см. рис. 2). Емкость k -ой ячейки определяется как емкость плоского конденсатора Ck = e (bk / ak) 1. Емкости подобных ячеек одинаковы, поэтому искомая емкость C = Ck m/n , где m - число векторных трубок; n - число потенциальных перепадов (число ячеек в одной трубке).

При построении векторных линий поля электронной линзы первые два правиле сохраняются. Однако требование постоянства потока в векторной трубке приводит к изменению условия подобия ячеек. Вычислим DyЕ в сечении А-А (рис.3):
DyЕ = Ek DSk = (DU/ak) 2 p rk bk = const .
Отсюда следует:
(bk / ak) rk = const = k, где rk - расстояние от центра ячейки до оси. Постоянная k вычисляется после построения трубки поля, которая образуется линией, совпадающей с осью симметрии, и первой векторной линией.
Экспериментальная установка
В работе исследуются двухпроводная передающая линия с проводами разного диаметра и электронная линза. В первом случае модель представляет собой два металлических цилиндра конечной длины, во втором случае два соосных полуцилиндра.
Распределение потенциала поля моделей находиться с помощью зонда, подключенного к потенциальному зажиму вольтметра. Эквипотенциали U = 0 и U=U0 совпадают с электродами. Остальные определяются с заранее выбранным шагом DU = U0/n.
Расчеты
-
Картину плоскопараллельного поля двухпроводной линии смотри на вкладыше.
-
Расчет максимальной и минимальной s на одном из проводов линии: s = e Еn для k-ой ячейки: En = DU/ak , где DU=Uk+1-Uk=1
smin = e DU/ ak max = 8.85 10-12 / 0.022 = 402.3 10-12 Кл/м2
smax = e DU/ ak min = 8.85 10-12 / 0.009 = 983.3 10-12 Кл/ м2
-
Расчет прогонной емкости двухпроводной линии ск = e bk /ak c = ck m/n
bk /ak =1, сk =8.85 10-12 Ф , с = 8.85 10-12 25/10 = 22.13 10-12 Ф.
-
Картину аксиально-симметричного поля электронной линзы смотри на вкладыше
Вывод
В данной работе мы исследовали двухпроводную передающую линию с проводами разного диаметра и электронную линзу. Убедились, что модели в электролитической ванне являются достаточно точными математическими аналогиями различного рода физических полей и поля электрического тока в проводящей среде. Убедились, что поверхностная плотность заряда максимальна на середине провода, а минимальна на концах. А так же рассчитали прогонную емкость двухпроводной передающей линии с = 22.13 10-12 Ф.
