Угловая модуляция

Угловая модуляция подразделяется на фазовую (ФМ) и частотную (ЧМ). При фазовой модуляции отклонение (сдвиг) фазы модулированного сигнала от линейной фазы изменяется пропорционально мгновенным значениям модулирующего сигнала а(t):

(3.8)

где k – коэффициент пропорциональности. Если а(t)=0, ФМ-колебание является простым гармоническим колебанием. С увеличением значений сигнала а(t) полная фаза растет во времени быстрее, чем по линейному закону. При уменьшении значений а(t) происходит спад скорости роста во времени. Наибольшее отклонение фазы модулированного сигнала от линейной фазы называется девиацией фазы _Д. Измеряется _Д в радианах в секунду и может принимать значения от единиц до десятков тысяч радиан в секунду. Математическая модель ФМ сигнала имеет вид

(3.9)

При частотной модуляции отклонение частоты модулированного сигнала от линейной зависимости ( ) изменяется пропорционально мгновенным значениям модулирующего сигнала а(t)

(3.10)

где k –коэффициент пропорциональности, называемый девиацией частоты _Д. Девиация частоты является одним из главных параметров частотных модуляторов и принимает значения от единиц герц до сотен мегагерц в модуляторах различного назначения. При ЧМ модуляции необходимо, чтобы всегда выполнялось условие _Д << ₀.

Полная фаза ЧМ сигнала с учетом выражений (3.1) и (3.10) находится путем интегрирования:

(3.11)

С учетом вышеизложенного математическая модель ЧМ сигнала запишется в виде

(3.12)

При модуляции несущей частоты одной гармоникой с учетом того, что из выражений (3.9) и (3.12) математические модели ФМ и ЧМ могут быть представлены в форме, похожей одна на другую:

(3.13)

где m – индекс модуляции. Для ФМ индекс модуляции m_ФМ = _Д , а для ЧМ индекс модуляции m_ЧМ = _Д/₀ , т.е. является амплитудой отклонения фазы, измеренной в радианах.

Таким образом, отличие ФМ и ЧМ модуляций заключается в следующем:

а) девиация частоты _Д ЧМ сигнала пропорциональна значению амплитуды низкочастотного сигнала, _Д = qU_ , где q – коэффициент пропорциональности;

б) значение _Д для ФМ сигнала пропорционально частоте низкочастотного сигнала, _Д = qU_ ₀. Здесь U_ – амплитуда низкочастотного сигнала.

Спектральная диаграмма угловой модуляции при f₀ = 2000 Гц и равенстве индексов модуляции m_ЧМ = m_ФМ = m приведена на рисунке 3.6.

Принцип реализации многоканальной системы с ФМ и ЧМ приведен на рисунке 3.7.

Как видно из структурной схемы (рис. 3.7), на одной несущей частоте (для примера возьмем n=1) формируются два частотных канала. Модель группового сигнала двух каналов для n-й несущей в этом случае имеет вид

(3.14)

Модель группового сигнала для N несущих

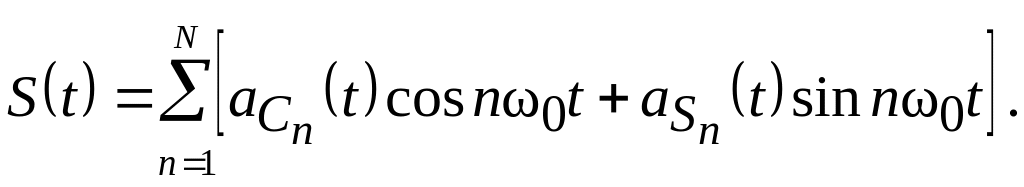(3.15)