8.4. Интегральные оценки качества

 

Интегральные оценки дают обобщенную оценку быстроты затухания и величины отклонения регулируемой величины, в виде единого числового значения.

Находят применение первые три из перечисленных в списке интегральные оценки:

и — линейные интегральные оценки (не чувствительны к высшим производным координат САУ).

и — квадратичные интегральные оценки (не чувствительны к высшим производным координат САУ).

— улучшенная квадратичная интегральная оценка (чувствительна к значению скоростной составляющей в движении координат САУ).

— интегральные оценки более высоких порядков (чувствительны к значению скорости, ускорению,... координат САУ).

Графическая интерпретация свойств линейной и квадратичной интегральных оценок представлена на рис. 7.

1. Пусть имеем переходные функции .

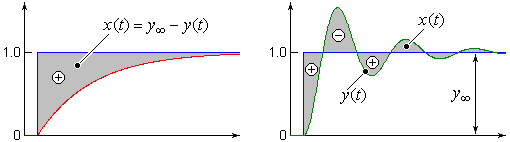
Рис. 7. Линейная и интегральная квадратичные оценки качества САУ

 

Рассмотрим линейные интегральные оценк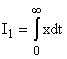и:

и .

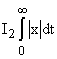Очевидно, что чем меньше значение оценки или , тем лучше переходный процесс, но:

a) Оценка не может применяться к колебательному переходному процессу.

b) Аналитическое вычисление оценки по коэффициентам уравнения ошибки затруднено.

c) Одно значение оценки может соответствовать переходным процессам с разной колебательностью (если совпадают мажоранты и миноранты).

2. Ограничения "a" и "b" для оценок и преодолеваются квадратичными интегральными оценками 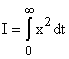и :

и ..

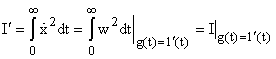Заметим, что оценку можно получить нахождением оценки , если подать на вход САУ не ступенчатую , а дельта функцию . Применение оценки ограничено тем, что она не чувствительна к установившемуся значению ошибки .

3. Ограничение "b" для оценок , , и снимается улучшенной квадратичной интегральной оценкой:

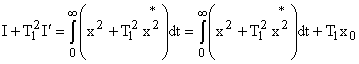
где: — начальное значение отклонения в переходном процессе.

Очевидно, что будет минимальна при . Решение этого дифференциального уравнения есть экспонента: , а .

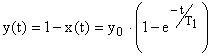Следовательно, улучшенная квадратичная интегральная оценка будет иметь минимум при приближении переходной функции к заданной экспоненте (с постоянной времени ).

4. Можно использовать улучшенные интегральные оценки более высоких порядков. Например:

.

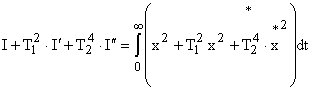Здесь оценка будет иметь минимум, только при перемещениях координат САУ с определенными скоростью и ускорением, которые определены постоянными времени и соответственно. Очевидно, что дифференциальным уравнением второго порядка можно определить желаемый переходный процесс с заданным затуханием.

Определение величин интегральных оценок может производиться аналитическими и численными методами. Последние заключаются в интегрировании величины ошибки САУ в процессе определения ее переходных характеристик. Аналитический расчет квадратичных интегральных оценок позволяет вычислять их величины непосредственно по передаточным функциям САУ.

Для аналитического расчета можно воспользоваться теоремой Парсеваля:

.

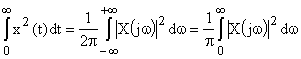Если ошибка , то ее изображение:

.

Для нахождения и мы должны подавать сигналы и . Их изображения Фурье соответственно равны:

и .

Тогда установившиеся значения выходной координаты и, соответственно, значения передаточная функция для этих режимов:

и .

В итоге изображения ошибок:

и

А квадратичные интегральные оценки определяются как:

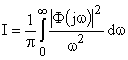и .
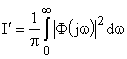