Критерии устойчивости
Рассмотрим 3 критерия устойчивости систем управления: критерий Рауса-Гурвица, Михайлова и Найквиста.
Критерии, использующие характеристическое уравнение системы
Первые 2 критерия используют характеристическое уравнение системы, получаемое путем приравнивания 0 знаменателя передаточной функции системы:
,
где
,
.
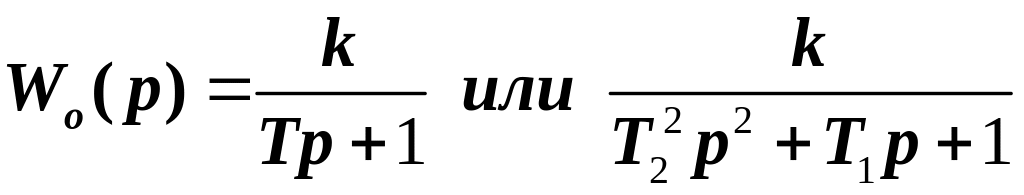С помощью функции feedback получаем передаточную функцию АСР. Отмерим, что ПФ объекта в данном случае задается без множителя запаздывания. Командой:
[num,den]=tfdata(sysAll,'v');
получим вектор коэффициентов знаменателя. Параметр 'v' нужен для того, чтобы получить коэффициенты в виде вектора, а не ячеек с содержанием вектора. Эти коэффициенты соответствуют коэффициентам характеристического уравнения системы.
Критерий Рауса-Гурвица
Не вдаваясь в теоретические подробности, критерий сводится к составлению определителя Гурвица и определению положительности соответствующих миноров. Для АСР 1-ого и 2-ого порядка с ПИ регулятором (как в прямом контуре, так и в контуре обратной связи) характеристическое уравнение будет иметь вид:
,
а их определители:
.
Если поставить коэф-ты в соответствии с записью векторов в MATLAB, то к соответствующему индексу надо прибавить 1.
М.б. два варианта решения проблемы:
1. Из коэф-тов вектора составляется определитель в виде квадратной матрицы и вычисляются определители всех диагональных алгебраических дополнений, путем пошагового удаления последней строки и последнего столбца. Все они должны быть больше 0 (положительны).
Длина вектора определяется функцией length(Nvec), а определитель вычисляется функцией det(mat).
2. Прямое сравнение коэффициентовтов. Для системы 1-ого порядка:
Для системы 2-ого порядка:
Критерий Михайлова
Для того чтобы
система была устойчива, необходимо и
достаточно, чтобы при
ее кривая Михайлова, начинаясь с
положительной вещественной полуплоскости,
последовательно обходила
квадрантов в положительном направлении
(против часовой стрелки). Следует
отметить, что кривые Михайлова устойчивых
систем не пересекают начало координат
и уходят на
в
-ом
квадранте.
Для использования
этого критерия в характеристическом
уравнении оператор Лапласа заменяется
на
,
Вследствие чего получим уравнение
годографа Михайлова:
.
Осуществляется это удовольствие циклом for:
for n=1:length(den)
Mih=Mih+den(n)*(j*omega).^(length(den)-n);
end
Выделяя вещественную
и мнимую части функциями real
и imag,
строим годограф Михайлова в координатах
.
Далее по графику считаем количество
пересеченных квадрантов.
Критерий Найквиста
Критерий можно записать так: если кривая АФЧХ разомкнутой АСР не охватывает точку (–1; j0), то замкнутая АСР является устойчивой.
Поэтому, строим диаграмму Найквиста для системы:
Nyquist(sysR*sysO), grid on
Значения для ω можно задавать и самостоятельно.