6.2. Основная теорема теории вычетов

     Как видно из определений (66)-(71), понятие и свойства вычетов оказываются очень полезным при вычислении контурных интегралов от функций комплексного переменного и в общем виде могут быть сформулированы как основная теорема о вычетах: если функция  является аналитической всюду в замкнутой области  , за исключением конечного числа изолированных особых точек , лежащих внутри  , то

(74)

     Пример 6-5. Вычислить интеграл  .

     Решение. Точка   является особой для подынтегральной функции, причем, согласно классификации, это полюс третьего порядка. Тогда

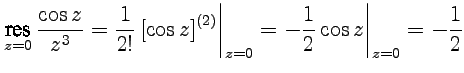
и соответственно  .

     Пример 6-6. Вычислить  .

     Решение. Особая точка подынтегральной функции определяется из уравнения  ,   (рис. 27). Чтобы выяснить характер этой точки, разложим функцию   в ряд Лорана по степеням  :

Рис.27

Так как функция  , следовательно:   - полюс первого порядка. Тогда с помощью (69) получим

     Пример 6-7. Вычислить интеграл  .

     Решение. Уравнение контура интегрирования можно привести к виду  , таким образом это окружность радиуса 2 с центром в точке   или   (рис.28). Уравнение   имеет четыре корня  ,  , которые являются простыми полюсами, так как  , при этом внутри контура находятся только два,   и  . Тогда по теореме о вычетах получим

Рис.28

     Пример 6-8. Вычислить интеграл  .

    Решение. Подынтегральная функция имеет 6 особых точек в окрестности  , которые все являются простыми полюсами, а точка  является устранимой,  . Внутри контура интегрирования находится 5 точек (  ), но в данном случае для вычисления интеграла удобнее воспользоваться теоремой (73), тогда

     Пример 6-9. Вычислить интеграл  .

     Решение. Подынтегральная функция в круге   имеет две особые точки:   и   . Найдем вычеты в этих точках:       1.   - так как эта точка является существенно особой, то вычет можно найти из определения (67). Тогда из разложений в ряд Лорана каждого сомножителя, получим

.

     2. . - простой полюс, следовательно:

Окончательно, применяя теорему о вычетах (74), получим

31) Интегралы виды   

     Для рациональной функции   указанные интегралы можно свести к контурным от функций комплексной переменной с помощью следующей замены переменных:

и так как   меняется в пределах от 0 до  , то точка   будет проходить окружность  . Тогда, после замены переменных в подынтегральном выражении

(75)

Обозначая

после применения теоремы о вычетах получим

где   - полюса функции  , принадлежащие области  .

     Пример 6-10. Вычислить интеграл  .

     Решение. После замены (75) интеграл преобразуется к следующему:

Уравнение   имеет корни  , которые, таким образом, являются простыми полюсами, причем внутрь контура интегрирования   попадает только одна точка  . Тогда по теореме о вычетах имеем: