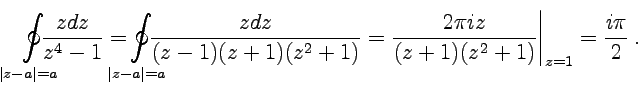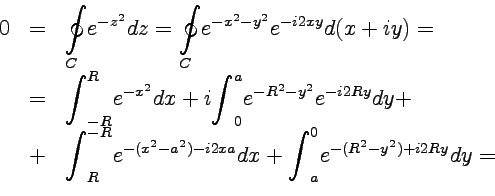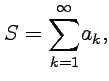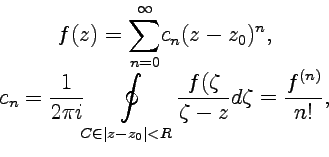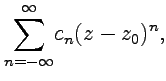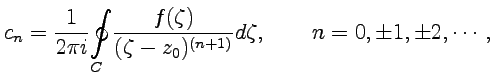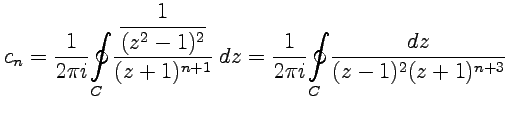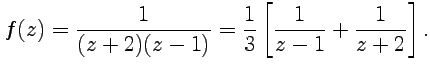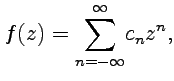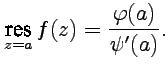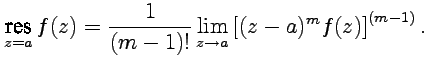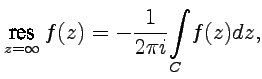16,18)
|
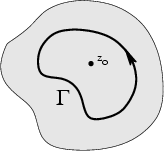
Пусть
на комплексной плоскости задана
кривая |
|
||
|
(43) |
|
||
Рис.13 |
|
|||
|
|
|
|
|
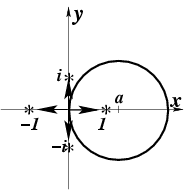
где ![]() .
Учитывая, что
.
Учитывая, что ![]() и,
следовательно,
и,
следовательно, ![]() ,
а также
,
а также ![]() ,
после подстановки интеграл (43)
может быть записан в форме:
,
после подстановки интеграл (43)
может быть записан в форме:
|
(44) |
и,
таким образом, сводится к вычислению
криволинейных интегралов второго рода
от действительных функций ![]() и
и ![]() по
контуру
.
Из определения (43),
или известных свойств криволинейных
интегралов следуют свойства интегралов
от функций комплексного переменного:
по
контуру
.
Из определения (43),
или известных свойств криволинейных
интегралов следуют свойства интегралов
от функций комплексного переменного:
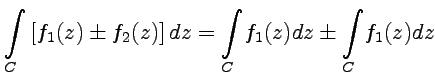
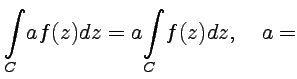 Const
Const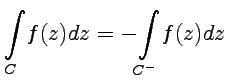 , где
, где  означает,
что направление обхода кривой
является
противоположным к
.
означает,
что направление обхода кривой
является
противоположным к
.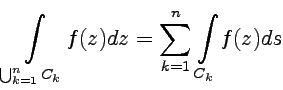 , т.
е. интеграл по кривой, составленной
из
частей
, т.
е. интеграл по кривой, составленной
из
частей 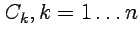 ,
равен сумме интегралов по отдельным
частям.
,
равен сумме интегралов по отдельным
частям.
При
параметрическом задании кривой
интегрирования ![]() ,
и тогда интеграл преобразуется к
определенному интегралу от комплекснозначной
функции действительной переменной
,
и тогда интеграл преобразуется к
определенному интегралу от комплекснозначной
функции действительной переменной ![]() вида:
вида:
|
(45) |
Пример 3-1. Пусть
-
простая замкнутая кривая на плоскости ![]() ,
которая захватывает площадь
,
которая захватывает площадь ![]() (рис.14).
Доказать следующие формулы:
(рис.14).
Доказать следующие формулы:
|
1. |
Рис.14 |
|
|
|
Решение.1. Запишем интеграл как два криволинейных
|
(46) |
Первый
интеграл в данном случае становится
обычным определенным интегралом ("по
оси ![]() ")
в пределах от минимального до максимального
значения проекции кривой
на
ось
,
а поскольку этот интеграл вычисляется
дважды в противоположных направлениях,
то он обращается в 0. Для вычисления
второго интеграла используем теорему
Стокса, которая в общем виде может быть
записана в векторной форме как
")
в пределах от минимального до максимального
значения проекции кривой
на
ось
,
а поскольку этот интеграл вычисляется
дважды в противоположных направлениях,
то он обращается в 0. Для вычисления
второго интеграла используем теорему
Стокса, которая в общем виде может быть
записана в векторной форме как
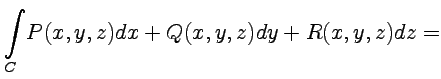
|
(47) |
где
в
(47)
- одна из трех независимых переменных ![]() (!).
Тогда второй интеграл после замены
(!).
Тогда второй интеграл после замены ![]() в
(47)
и вычисления определителя принимает
вид
в
(47)
и вычисления определителя принимает
вид

так как в силу произвольного вида поверхности в (47) она может быть выбрана в виде плоской области .
2.
Интеграл может быть вычислен аналогично
первой задаче, либо в данном случае
можно заметить, что умножение всех
комплексных чисел плоскости ![]() на
на ![]() геометрически
будет эквивалентно повороту системы
координат
геометрически
будет эквивалентно повороту системы
координат ![]() на
на ![]() против
часовой стрелки, а так как сама функция
и кривая остаются неизмененными, то
результат задачи можно получить, умножив
ответ задачи 1 на
и
тогда
против
часовой стрелки, а так как сама функция
и кривая остаются неизмененными, то
результат задачи можно получить, умножив
ответ задачи 1 на
и
тогда ![]() .
.
3. Результат можно получить, комбинируя результаты задач 1 и 2:
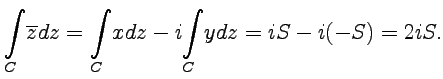
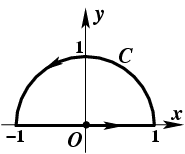
Пример 3-2. Вычислить
интеграл 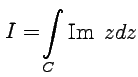 ,
если
-
дуга полуокружности
,
если
-
дуга полуокружности ![]() (рис.15).
(рис.15).
Решение. На
основе формулы (44),
с использованием ![]() и
уравнения окружности
и
уравнения окружности ![]() ,
получим
,
получим
|
|
Рис.15 |
|
|
|
Возможен
более быстрый способ вычисления
интеграла, если использовать результат
второй задачи примера 4-1 и общие свойства
интегралов от функций комплексной
переменной. Действительно, рассмотрим
интеграл по полной окружности ![]() ,
и так как площадь
,
и так как площадь ![]() ,
то получим
,
то получим

так
как полная окружность состоит из двух
полуокружностей в верхней ![]() и
нижней полуплоскости
и
нижней полуплоскости ![]() ,
которые переходят друг в друга со сменой
направления обхода на противоположное,
а подынтегральная функция на
кривых
и
,
которые переходят друг в друга со сменой
направления обхода на противоположное,
а подынтегральная функция на
кривых
и ![]() отличается
только знаком.
отличается
только знаком.
Рассмотрим вычисление интеграла с помощью формулы (45) при параметрическом задании кривой. Тогда:

и после такой замены интеграл преобразуется следующим образом:

где первый интеграл исчезает, так как с помощью формулы Эйлера (11) он сводится к двум интегралам по полному периоду от действительных периодических функций.
Пример 3-3. Вычислить интегралы

по
радиусу-вектору точки ![]() .
.
Решение. С
помощью формулы (44)
и уравнения прямой, проходящей через
точки ![]() и
и ![]() :
:
![]() ,
получим
,
получим

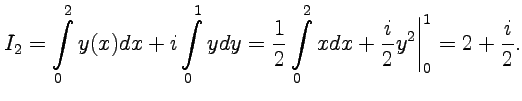
Пример 3-4. Вычислить
интеграл 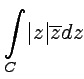 ,
где
-
замкнутый контур, который состоит из
верхней полуокружности
и
отрезка
,
где
-
замкнутый контур, который состоит из
верхней полуокружности
и
отрезка![]() .
.
Решение. Согласно общим свойствам интегралов от функций комплексного переменного, интеграл задачи может быть представлен в виде суммы двух интегралов по каждому из двух участков:
|
|
Пример 3-5. Доказать,
что интеграл 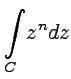 ,
где
-
натуральное число, не зависит от формы
кривой
.
,
где
-
натуральное число, не зависит от формы
кривой
.
Решение. Рассмотрим
сначала частный случай с ![]() ,
Тогда по определению интеграла, задавая
некоторое разбиение кривой
,
получим
,
Тогда по определению интеграла, задавая
некоторое разбиение кривой
,
получим
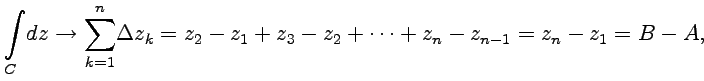
где ![]() и
и ![]() -
начальная и конечная точки кривой
.
Таким образом, значение интеграла
определяется только точками
и
,
но не формой кривой, которая их соединяет.
-
начальная и конечная точки кривой
.
Таким образом, значение интеграла
определяется только точками
и
,
но не формой кривой, которая их соединяет.
Общий
случай: функция ![]() является
дифференцируемой (пример 2-7)
и так как
является
дифференцируемой (пример 2-7)
и так как ![]() ,
то подынтегральное выражение можно
аппроксимировать как
,
то подынтегральное выражение можно
аппроксимировать как 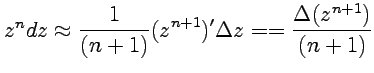
![]() и
соответственно представить интеграл
как сумму следующего вида:
и
соответственно представить интеграл
как сумму следующего вида:

На
основе такого результата также можно
получить интересное следствие, что если
кривая
является
замкнутой, то имеет место свойство![]() ,
и, кроме того, этот результат будет
справедливым и для любой функции вида
,
и, кроме того, этот результат будет
справедливым и для любой функции вида 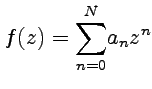 ,
а также для сходящихся рядов при
,
а также для сходящихся рядов при ![]() .
.
19 Результат,
полученный в примере 3-5,
является частным случаем теоремы Коши
и, если
является
аналитической (или только дифференцируемой)
функцией в области ![]() комплексной
плоскости, то интеграл по любой замкнутой
кривой
комплексной
плоскости, то интеграл по любой замкнутой
кривой ![]() от
равен
нулю:
от
равен
нулю:
|
(48) |
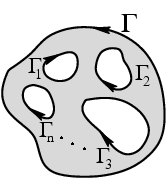
Теорема Коши имеет несколько важных следствий:
|
|
|
||
|
(49) |
|
||
Рис.17 |
|
|||
|
|
|
|
|
где
все участки границы обходятся в
положительном направлении, т. е. когда
захватываемая область остается слева
при движении вдоль каждой кривой ![]() ;
значение
интеграла
;
значение
интеграла ![]() от
функции
по
некоторой кривой, соединяющей точки
от
функции
по
некоторой кривой, соединяющей точки ![]() и
,
т. е.:
и
,
т. е.:
|
(50) |
будет
аналитической функцией переменной
,
причем ![]() . Функция
(50)
называется первообразной,
и для нее имеет место комплексный аналог
формулы Ньютона-Лейбница:
. Функция
(50)
называется первообразной,
и для нее имеет место комплексный аналог
формулы Ньютона-Лейбница:
|
(51) |
Пример 3-6. Вычислить
интеграл от функции 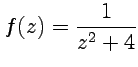 по
контуру
по
контуру ![]() .
.
Решение. Так
как ![]() в
точках
в
точках ![]() ,
то внутри круга
подынтегральная
функция будет аналитической во всех
точках. Тогда, по теореме Коши (48)
интеграл:
,
то внутри круга
подынтегральная
функция будет аналитической во всех
точках. Тогда, по теореме Коши (48)
интеграл:
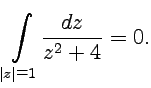
Пример
3-7. Вычислить
интеграл 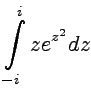 .
.
Решение. Функция ![]() является
аналитической, так как, согласно свойствам
аналитических функций,
-
это произведение аналитической
функции
является
аналитической, так как, согласно свойствам
аналитических функций,
-
это произведение аналитической
функции ![]() и
сложной функции, построенной из двух
аналитических
и
сложной функции, построенной из двух
аналитических ![]() и
и ![]() :
: ![]() ;
формальное дифференцирование (28)
также дает результат
;
формальное дифференцирование (28)
также дает результат  .
Следовательно, интеграл может быть
вычислен с помощью формулы Ньютона-Лейбница
(51):
.
Следовательно, интеграл может быть
вычислен с помощью формулы Ньютона-Лейбница
(51):
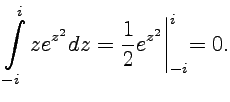
Пример
3-8. Вычислить
интеграл  по
контуру
,
изображенному на рис.18.
по
контуру
,
изображенному на рис.18.
Решение. Определим каждый участок контура параметрически:
|
|
|||
Рис.18 |
тогда интеграл запишется как сумма |
|||
|
||||
20) |
||||
|
Теорема Коши позволяет также установить связь между значениями аналитической функции во внутренних точках области ее определения и граничными значениями. При этом имеет место следующее соотношение (рис.19): |
|
||
|
(52) |
|
||
Рис.19 |
|
|||
|
|
|
|
|
Формула
(52)
называется интегральной
формулой Коши или интегралом
Коши.
Если в качестве контура ![]() в
(52)
выбрать окружность
в
(52)
выбрать окружность ![]() ,
то, заменяя
,
то, заменяя ![]() и
учитывая, что
и
учитывая, что ![]() -
дифференциал длины дуги
,
интеграл Коши можно представить в виде
формулы среднего значения:
-
дифференциал длины дуги
,
интеграл Коши можно представить в виде
формулы среднего значения:
|
(53) |
Формула Коши может быть расширена для производных аналитической функции , и так как входит в интеграл (52) как параметр, то на основе свойств интегралов, зависящих от параметра, после -кратного дифференцирования, можно получить
|
(54) |
Помимо
самостоятельного значения интегральной
формулы Коши, (52),
(54)
фактически дают очень удобный способ
вычисления контурных интегралов,
которые, как видно, будут выражаться
через значение "остатка"
подынтегральной функции в точке, где
эта функция имеет особенность![]() .
.
Пример
3-9. Вычислить
интеграл от функции
по
контуру ![]() (рис.20).
(рис.20).
Решение. Точка ![]() ,
в которой функция
,
в которой функция ![]() имеет
особенность, в отличие от примера 4-1,
находится внутри окружности
.
Представим интеграл в форме (52):
имеет
особенность, в отличие от примера 4-1,
находится внутри окружности
.
Представим интеграл в форме (52):
|
|
Рис.20 |
|
|
|
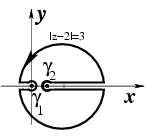
Пример 3-10. Вычислить
интеграл 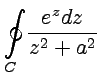 ,
если круг
,
если круг ![]() находится
внутри контура интегрирования
.
находится
внутри контура интегрирования
.
Решение. Подынтегральная
функция содержит особенности в
точках |
|
Рис.21 |
|
|
|
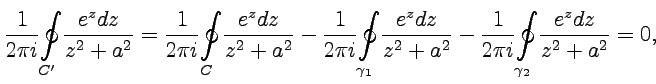
где
знаки во втором и третьем интегралах
учитывают, что направление обхода
контуров ![]() отрицательное,
а интегралы по берегам разрезов взаимно
уничтожаются. Для интегралов по
получим
отрицательное,
а интегралы по берегам разрезов взаимно
уничтожаются. Для интегралов по
получим

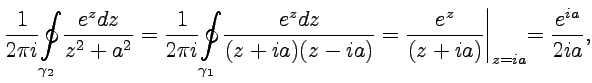

Отметим, что рассмотренный способ применения теоремы Коши в то же время является доказательством следствия (49).
Пример 3-11. Вычислить 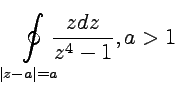 .
.
Решение. Найдем
решения уравнения |
|
|
|
|
|
Рис.22 |
|
|
|
|
|
Пример
3-12. Вычислить
интеграл  .
.
Решение. Точка ![]() находится
внутри контура интегрирования, который
является окружностью, но так как
знаменатель содержит степень, то для
вычисления интеграла в данном случае
необходимо использовать интегральную
формулу Коши для производной (54).
Тогда
находится
внутри контура интегрирования, который
является окружностью, но так как
знаменатель содержит степень, то для
вычисления интеграла в данном случае
необходимо использовать интегральную
формулу Коши для производной (54).
Тогда
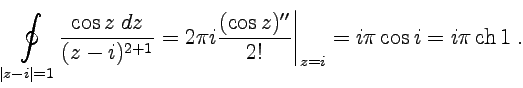
Пример
3-13. Вычислить
интеграл 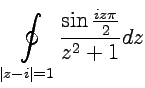 .
.
Решение. Знаменатель ![]() обращается
в ноль в точках
обращается
в ноль в точках ![]() ,
и так как контур интегрирования
представляет собой окружность радиуса
1 с центром в точке
,
и так как контур интегрирования
представляет собой окружность радиуса
1 с центром в точке ![]() ,
то внутрь попадает только точка
,
то внутрь попадает только точка ![]() .
Тогда, учитывая, что
.
Тогда, учитывая, что ![]() ,
по формуле Коши (52)
получим
,
по формуле Коши (52)
получим

Пример 3-14. Вычислить
интеграл 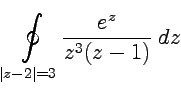 .
.
Решение. Знаменатель
подынтегрального выражения обращается
в ноль в точках |
|
Рис.23 |
|
|
|

Во многих важных случаях интегралов от функций действительной переменной оказывается удобным рассмотреть некоторые вспомогательные интегралы от комплексных функций.
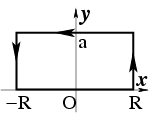
Пример 3-15. Вычислить
интеграл 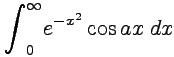 ,
используя известный результат для
интеграла Пуассона
,
используя известный результат для
интеграла Пуассона  .
.
Решение. Для
вычисления интеграла рассмотрим
вспомогательную функцию ![]() и
проинтегрируем ее по границе прямоугольной
области
и
проинтегрируем ее по границе прямоугольной
области ![]() ,
, ![]() (рис.24).
Тогда,по теореме Коши (48)
получим
(рис.24).
Тогда,по теореме Коши (48)
получим
|
|
Рис.24 |
|
|
|

Перейдем
к пределу ![]() ,
тогда, так как
,
тогда, так как 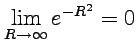 ,
то последний интеграл исчезает, и,
учитывая значение интеграла Пуассона,
получим
,
то последний интеграл исчезает, и,
учитывая значение интеграла Пуассона,
получим

и
после разделения действительной и
мнимой частей, а также учитывая, что
функция ![]() четная:
четная:

22) Числовым рядом комплексных чисел называется ряд вида:
|
(55) |
где ![]() -
последовательность комплексных чисел.
Необходимым и достаточным условием
сходимости ряда (55)
является критерий Коши, согласно
которому ряд
(55)
сходится тогда и только тогда, если
для
-
последовательность комплексных чисел.
Необходимым и достаточным условием
сходимости ряда (55)
является критерий Коши, согласно
которому ряд
(55)
сходится тогда и только тогда, если
для ![]() можно
указать такой номер
можно
указать такой номер ![]() ,
что
,
что 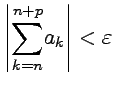 при
при ![]() и
любом натуральном
и
любом натуральном ![]() .
.
Ряд
(55)
называется абсолютно сходящимся,
если сходится ряд модулей 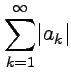 .
.
Решение задач, связанных с исследованием сходимости числовых рядов, основано на использовании признаков:
Д'Аламбера : ряд сходится, если начиная с некоторого , отношение
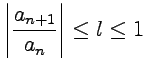 ,
, 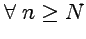 ;
;Коши : ряд сходится, если
 ,
;
,
;
а
также необходимого
условия сходимости : ![]() .
.
Пример 4-1. Исследовать сходимость следующих числовых рядов:
1.  ;
2.
;
2. 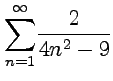 ;
3.
;
3. 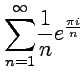 .
.
Решение. С помощью признака ДэАламбера получим:
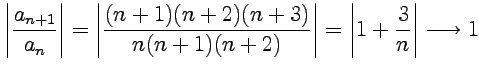
и аналогично для второго примера:

В третьем случае удобнее воспользоваться необходимым условием сходимости. Тогда после преобразования слагаемых ряда с помощью формулы Эйлера (11) :
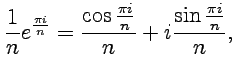
найдем,
что при ![]()
 и,
следовательно, ряд будет расходиться
как ряд обратных степеней, что показано
в математическом анализе, хотя второе
слагаемое
и,
следовательно, ряд будет расходиться
как ряд обратных степеней, что показано
в математическом анализе, хотя второе
слагаемое 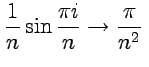 будет
давать сходящуюся часть полного ряда.
будет
давать сходящуюся часть полного ряда.
23)
Важным
случаем функциональных рядов  являются
степенные ряды, для которых
являются
степенные ряды, для которых ![]() .
Члены степенного ряда являются
аналитическими функциями, и, следовательно,
для таких рядов будут выполняться все
отмеченные теоремы и свойства. Поскольку
вид функций
.
Члены степенного ряда являются
аналитическими функциями, и, следовательно,
для таких рядов будут выполняться все
отмеченные теоремы и свойства. Поскольку
вид функций ![]() фиксирован,
то сходимость степенных рядов будет
определяться только видом его
коэффициентов
фиксирован,
то сходимость степенных рядов будет
определяться только видом его
коэффициентов ![]() ,
при этом множество точек, определяемых
условием
,
при этом множество точек, определяемых
условием ![]() ,
, ![]() ,
в которых ряд
,
в которых ряд 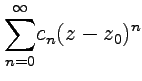 сходится,
называется кругом
сходимости и
соответственно
сходится,
называется кругом
сходимости и
соответственно ![]() -радиусом
сходимости.
Радиус сходимости степенного ряда
определяется с помощью формулы
Коши-Адамара:
-радиусом
сходимости.
Радиус сходимости степенного ряда
определяется с помощью формулы
Коши-Адамара: ![]() ,
где
,
где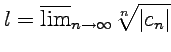 -
верхний предел последовательности
-
верхний предел последовательности ![]() .
.
Пример
4-2. Найти
радиус сходимости ряда 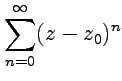 и
вычислить его сумму.
и
вычислить его сумму.
Решение. По признаку Д'Аламбера получим
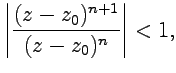
следовательно,
ряд сходится в круге ![]() ,
при этом его сумма будет аналитической
функцией в этом круге. Сумму ряда вычислим
как предел частичной суммы:
,
при этом его сумма будет аналитической
функцией в этом круге. Сумму ряда вычислим
как предел частичной суммы:
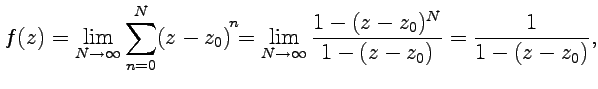
где
было использовано выражение для суммы
геометрической прогресии. Частный
случай рассмотренного ряда при ![]() :
:
|
(58) |
играет в дальнейших приложениях очень важную роль и будет использоваться довольно часто.
Если функция является аналитической, то ей всегда можно сопоставить степенной ряд, который в каждой точке области определения этой функции будет сходиться к ее значению в этой точке:
|
(59) |
где интеграл в (59) вычисляется по любой замкнутой кривой, принадлежащей области . Разложение функции , аналитической в круге , в сходящийся степенной ряд (59) называется разложением Тэйлора, а ряд - рядом Тэйлора.
Пример
4-3. Разложим
в ряд Тэйлора функцию 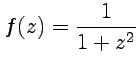 .
.
Решение. Функция
является
аналитической на всей комплексной
плоскости, за исключением точек ![]() .
Поэтому в любом круге, не
содержащем
.
Поэтому в любом круге, не
содержащем ![]() ,
функцию можно разложить в степенной
ряд. Рассмотрим круг
,
функцию можно разложить в степенной
ряд. Рассмотрим круг ![]() .
Используя ряд геометрической прогрессии
(58)
с заменой
.
Используя ряд геометрической прогрессии
(58)
с заменой ![]() ,
получим
,
получим
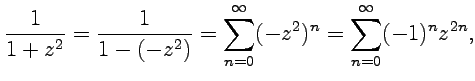
при
этом по формуле Коши-Адамара радиус
сходимости ![]() .
Чтобы найти разложение в круге
.
Чтобы найти разложение в круге ![]() ,
преобразуем функцию, разлагая на простые
дроби:
,
преобразуем функцию, разлагая на простые
дроби:
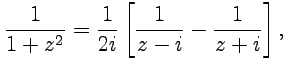
и тогда с учетом определения области разложения и на основе формулы (58):
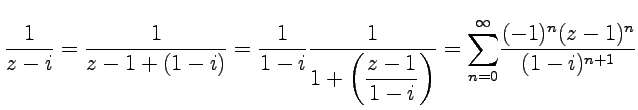
и
аналогично 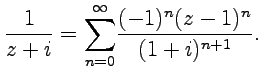 Тогда
для функции получим разложение:
Тогда
для функции получим разложение:

Найдем
радиус сходимости полученного степенного
ряда. Для этой цели преобразуем слагаемые,
используя ![]() .
Тогда ряд можно переписать в виде
.
Тогда ряд можно переписать в виде

и по формуле Коши-Адамара получим
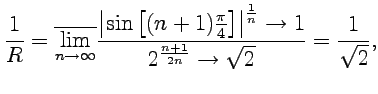
что соответствует условиям примера.
Пример 4-4. Найти радиусы сходимости степенных рядов:
1. 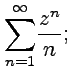 2.
2. 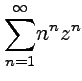 .
.
Решение
На основании формулы Коши-Адамара имеем
Т. Е. Ряд сходится в круге радиуса 1.
аналогично для радиуса сходимости можно получить
![]()
таким образом сумму ряда можно вычислить только в одной точке
Пример 4-5. Разложить
в ряд функцию 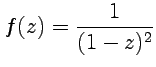 .
.
Решение. Применяя два раза ряд геометрической прогресии (58), получим
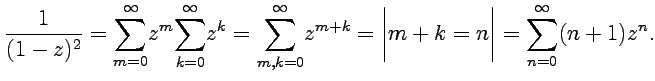
Этот
же результат можно получить на основе
соотношения  ,
и дифференцируя ряд (58):
,
и дифференцируя ряд (58):
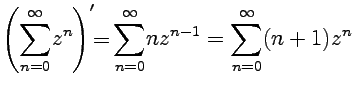
Пример
4-6. Разложить
в ряд по степеням
функцию  .
.
Решение. Представим функцию в виде суммы простых дробей:
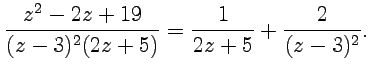
Используя ряд геометрической прогрессии (58):
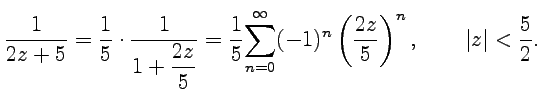
Разложение для второй дроби можно также получить с помощью ряда геометрической прогрессии, если учесть, что
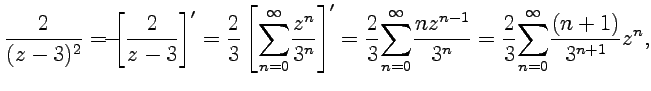
и
согласно условиям сходимости геометрической
прогресии (58), ![]() .
Складывая полученные ряды и объединяя
области сходимости, получим окончательно:
.
Складывая полученные ряды и объединяя
области сходимости, получим окончательно:

Пример
4-7. Разложить
в ряд Тэйлора функцию ![]() .
.
Решение. Показательная
функция является аналитической во всей
комплексной плоскости, и тогда ее
разложение в ряд по степеням
может
быть получено напрямую с помощью формул
(59),
и так как 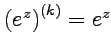 ,то
,то ![]() и
и

Аналогично можно получить разложения других элементарных функций:
1. 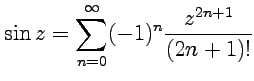
2. 
3. 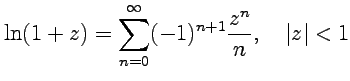
4. 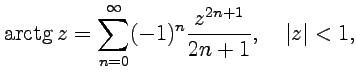
которые встречаются достаточно часто в дальнейших приложениях.
Пример 4-8. Разложить
функцию 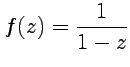 в
ряд по степеням
в
ряд по степеням ![]() для
для ![]() и
определить радиус сходимости ряда.
и
определить радиус сходимости ряда.
Решение. Чтобы
получить разложение функции в окрестности
указанной точки, т. е. в форме 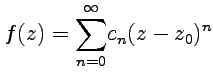 ,
преобразуем выражение для функции:
,
преобразуем выражение для функции:

Из
условия сходимости ряда геометрической
прогресии (58)
получим, что для его применимости в
данном случае должно выполняться
условие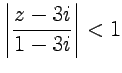 или
или ![]() .
Тогда в указанном круге:
.
Тогда в указанном круге:
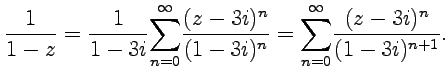
24) Как уже отмечалось, аналитической функции всегда можно сопоставить степенной ряд , который сходится к функции окрестности точки или в круге . Точка такого типа называется правильной точкой функции . Например, все точки будут правильными для функции , как это следует из свойств ряда (58). Таким образом, с помощью степенных рядов можно исследовать поведение функции в окрестности ее правильных точек. Наоборот, точки, которые не являются правильными для функции , называются ее особыми точками. Так, для ряд (58) не будет сходиться, а для функции эта точка будет особой. Поведение функции в окрестности ее особой точки можно исследовать с помощью ряда Лорана, который определяется как степенной ряд следующего вида:
|
(60) |
при этом называют
 -
главной;
-
главной;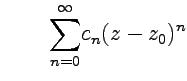 -
правильной
-
правильной
частью ряда. Из определения следует, что областью сходимости ряда Лорана (60) будет пересечение областей сходимости его частей и имеет место теорема:
функция
аналитическая
в круговом кольце ![]() однозначно
представляется в этом кольце сходящимся
рядом Лорана, а коэффициенты определяются
выражением:
однозначно
представляется в этом кольце сходящимся
рядом Лорана, а коэффициенты определяются
выражением:
|
(61) |
где - произвольный замкнутый контур, принадлежащий кольцу . Формула (61) определяет прямой способ разложения функции в ряд Лорана.
Пример
5-1. Разложить
в ряд Лорана функцию 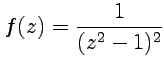 в
кольце
в
кольце ![]() .
.
Решение. Область
представляет собой круг радиуса 2 с
центром в точке ![]() (рис.25),
которая для функции является особой.
Из формулы для коэффициентов разложения
(61)
получим
(рис.25),
которая для функции является особой.
Из формулы для коэффициентов разложения
(61)
получим
|
|
Рис.25 |
|
|
|
и для вычисления интеграла необходимо рассмотреть несколько случаев:
1. ![]() -
подынтегральная функция является
аналитической всюду в кольце
и
по теореме Коши
-
подынтегральная функция является
аналитической всюду в кольце
и
по теореме Коши ![]() для
для![]() ;
;
2. ![]() -
для вычисления интеграла воспользуемся
формулой (54):
-
для вычисления интеграла воспользуемся
формулой (54):
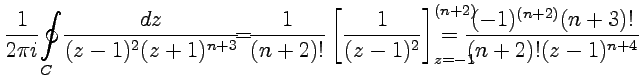
и,
после подстановки
,
получим  для
для ![]() .
Таким образом, разложение функции в ряд
Лорана запишется в виде
.
Таким образом, разложение функции в ряд
Лорана запишется в виде 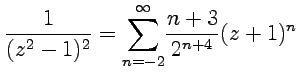 или,
отделяя отрицательные степени:
или,
отделяя отрицательные степени:

Разложение в ряд Лорана, полученное в примере, основано на прямом вычислении коэффициентов в (60). С другой стороны, для многих практически важных случаев более удобным является использование некоторых стандартных разложений. Например, уже применявшийся при разложении функций в ряд Тэйлора ряд геометрической прогрессии
|
(62) |
разложение
основных элементарных функций ![]() ,
, ![]() ,
, ![]() с
заменой переменных, которая обеспечивает
сходимость соответствующих степенных
рядов, метод неопределенных коэффициентов,
дифференцирование рядов для вспомогательных
функций и т. д.
с
заменой переменных, которая обеспечивает
сходимость соответствующих степенных
рядов, метод неопределенных коэффициентов,
дифференцирование рядов для вспомогательных
функций и т. д.
Пример 5-2. Разложить в ряд Лорана функцию в кольце .
Решение. Чтобы
разложить функцию в ряд по степеням ![]() ,
преобразуем функцию, чтобы привести ее
к виду, допускающему использование
стандартных разложений.
,
преобразуем функцию, чтобы привести ее
к виду, допускающему использование
стандартных разложений.

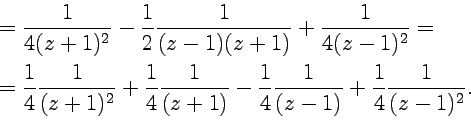
Первые
два слагаемых уже не требуют разложения,
так как имеют вид слагаемых ряда Лорана
с ![]() .
Для того чтобы получить разложение
третьего слагаемого, необходимо
преобразовать его так, чтобы можно было
использовать ряд геометрической
прогресии (58),
сходящийся в кольце
.
Тогда
.
Для того чтобы получить разложение
третьего слагаемого, необходимо
преобразовать его так, чтобы можно было
использовать ряд геометрической
прогресии (58),
сходящийся в кольце
.
Тогда
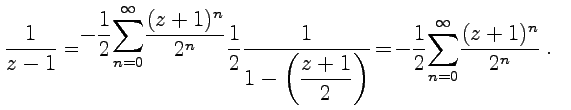
Разложение четвертого слагаемого можно получить дифференцированием ряда для третьего:
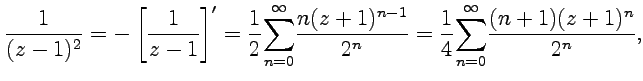
и после сложения результатов для отдельных слагаемых разложение запишется как
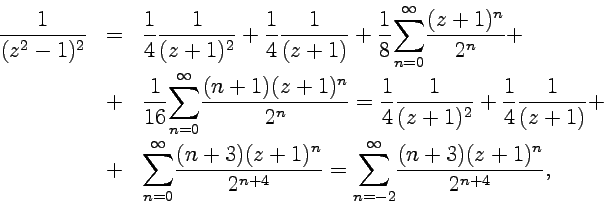
что совпадает с разложением, полученным в примере 5-1.
Пример
5-3. Найти
все разложения в ряд Лорана по
степеням
функции  .
.
Решение. Уравнение ![]() имеет
корни
имеет
корни ![]() ,
тогда
,
тогда
|
|
|
Особые
точки
определяют
три области на комплексной плоскости
(рис.26),
где должны быть получены независимые
разложения. Область I ( |
|
|
Рис.26 |
|
|
|
|
|
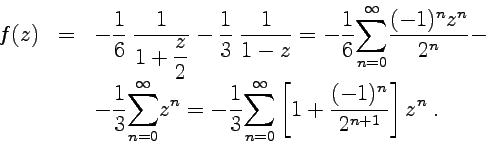
Область
II (![]() ):
):

Область
III ( ![]() ):
):
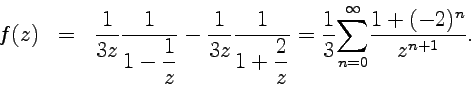
Разложение для первой области не содержит отрицательных степеней и является рядом Тэйлора.
Пример 5-4. Разложить
функцию ![]() в
ряд Лорана в окрестности точек: 1)
,
2)
в
ряд Лорана в окрестности точек: 1)
,
2) ![]() ,
3)
,
3) ![]() ,
4) в кольце
,
4) в кольце![]() .
.
Решение. С помощью метода неопределенных коэффициентов можно представить в виде
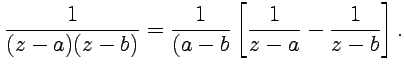
1. В окрестности для первого и второго слагаемого получим
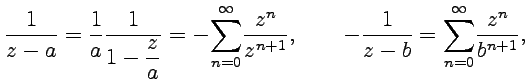
и тогда
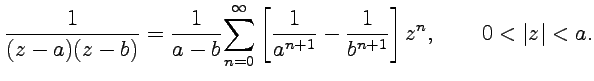
2.
В окрестности
разложим
второе слагаемое в ряд по степеням ![]() :
:
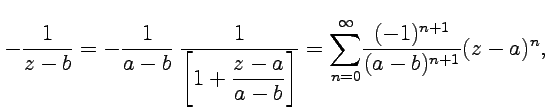
и
тогда полное разложение для ![]() запишется
как
запишется
как
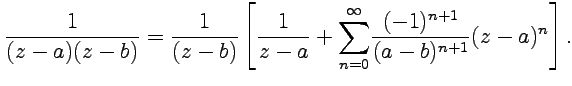
3. В окрестности разложение для первого слагаемого принимает вид
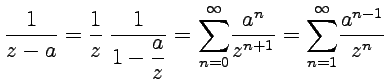
и аналогично для второго, что дает ряд Лорана для функции в виде
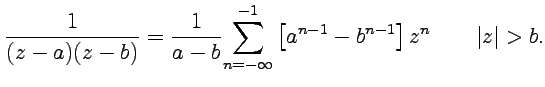
4.
Разложение для кольца ![]() можно
получить, используя уже полученные ряды
для первого слагаемого (область 3) и
второго слагаемого (область 1):
можно
получить, используя уже полученные ряды
для первого слагаемого (область 3) и
второго слагаемого (область 1):
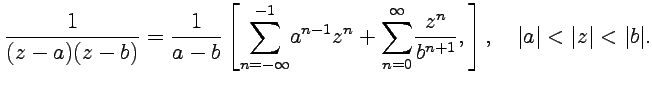
Пример 5-5. Найти
первые три слагаемых ряда Лорана для
функции 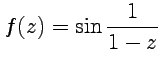 в
окрестности точки
.
в
окрестности точки
.
Решение. В
кольце ![]() функция
является аналитической, и следовательно,
допускает разложение в ряд Лорана.
Тогда, используя разложение функции
функция
является аналитической, и следовательно,
допускает разложение в ряд Лорана.
Тогда, используя разложение функции ![]() в
ряд Тэйлора по степеням
в
ряд Тэйлора по степеням ![]() (пример
4-6) и заменяя далее
(пример
4-6) и заменяя далее 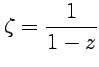 ,
получим
,
получим
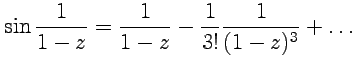
Далее,
разлагая каждое слагаемое в области ![]() ,
имеем, учитывая пример 5-2:
,
имеем, учитывая пример 5-2:
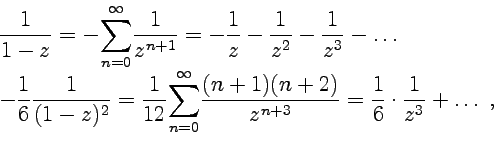
и так как остальные слагаемые разложения будут содержать более высокие степени, то для первых трех получим

Пример 5-6. Разложить
в ряд Лорана функцию  (
(![]() ,
, ![]() -натуральное
число) в окрестности точек
и
.
-натуральное
число) в окрестности точек
и
.
Решение. Чтобы
получить разложение, продифференцируем ![]() раз
функцию
раз
функцию ![]() : ,
тогда:
: ,
тогда:
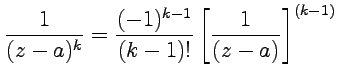
1) ![]()
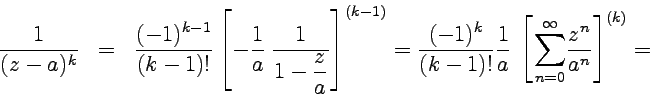

Заменим
индексы суммирования в полученном
разложении : ![]() ,
, ![]() ,
, ![]() ,
тогда
,
тогда
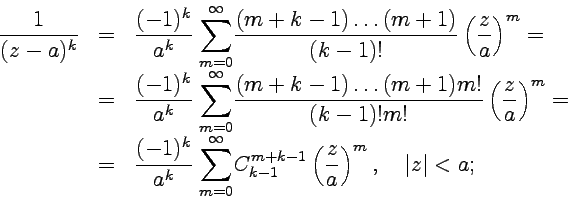
2)
разложение ![]() можно
получить, повторив аналогичные вычисления,
или на основе формальной замены
можно
получить, повторив аналогичные вычисления,
или на основе формальной замены ![]() и
тогда
и
тогда

Пример
5-7. Найти
радиус сходимости ряда Лорана 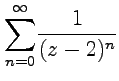 .
.
Решение. Ряд
Лорана в данном случае представлен
только главной частью. После замены
переменных 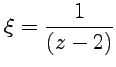 ряд
запишется как степенной
ряд
запишется как степенной 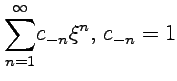 ,
и тогда радиус сходимости можно будет
найти с помощью формулы Коши-Адамара:
,
и тогда радиус сходимости можно будет
найти с помощью формулы Коши-Адамара:
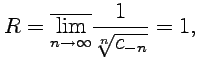
т.
е. ![]() ,
и, следовательно, круг сходимости ряда
Лорана
,
и, следовательно, круг сходимости ряда
Лорана ![]() .
.
25) В некоторых из рассмотренных выше примеров ряд Лорана содержал лишь конечное число слагаемых с отрицательными степенями, которые были записаны отдельно. Общий случай допускает различные варианты, которые составляют основу классификации изолированных особых точек аналитической функции и будут далее приведены в форме основных определений и теорем.
Точка
называется
изолированной особой точкой функции
,
если
является
однозначной и аналитической в кольце ![]() ,
а
-
особая для
,
и функция может быть не определена в
этой точке. Форма ряда Лорана в этом
случае определяет следующие случаи:
,
а
-
особая для
,
и функция может быть не определена в
этой точке. Форма ряда Лорана в этом
случае определяет следующие случаи:
(a)
ряд Лорана для функции
не
имеет слагаемых с отрицательными
степенями. В этом случае предельное
значение функции
в
точке ![]() либо
существует, или в этой точке функция
может быть доопределена. Такая особая
точка называется устранимой
особой точкой;
либо
существует, или в этой точке функция
может быть доопределена. Такая особая
точка называется устранимой
особой точкой;
(b)
ряд Лорана для функции
имеет
конечное число ![]() слагаемых
с отрицательными степенями. Тогда особая
точка
называетсяполюсом
порядка
функции
,
которая в этом случае может быть записана
в форме:
слагаемых
с отрицательными степенями. Тогда особая
точка
называетсяполюсом
порядка
функции
,
которая в этом случае может быть записана
в форме:
|
(63) |
где![]() функция
- аналитическая и
функция
- аналитическая и ![]() .
Обратное утверждение состоит в том, что
если
-
полюс порядка
функции
,
то для функции
.
Обратное утверждение состоит в том, что
если
-
полюс порядка
функции
,
то для функции 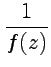 точка
-
ноль порядка
;
точка
-
ноль порядка
;
(c)
ряд Лорана для функции
имеет
бесконечное число слагаемых с
отрицательными степенями ![]() .
Точка
называетсясущественно
особой точкой
.
.
Точка
называетсясущественно
особой точкой
.
В
окрестности существенно особой точки
функции
в
зависимости от выбора последовательности,
аргумента, сходящейся к
,
последовательность значений функции
может сходиться к различным пределам,
в том числе и к произвольно выбранному
комплексному числу, включая бесконечность
(теорема
Сохоцкого-Вейерштрасса).
Для бесконечно удаленной точки определение
и классификация в определенном смысле
обратны к уже рассмотренным.
Тогда точка
называется
изолированной особой точкой однозначной
аналитической функции
,
если существует такое значение
,
что в области ![]() функция
не имеет особых точек, находящихся на
конечном расстоянии от точки
,
и
в
области
функция
не имеет особых точек, находящихся на
конечном расстоянии от точки
,
и
в
области ![]() можно
представить в виде ряда Лорана
можно
представить в виде ряда Лорана
|
(64) |
при этом если:
(a) ряд Лорана (64) не имеет слагаемых с положительными степенями, то называется устранимой особой точкой функции ; (b) ряд Лорана (64) имеет конечное число слагаемых с положительными степенями, то называется полюсом порядка функции , а функция может быть представлена в виде:
|
(65) |
где ![]() -
аналитическая и
-
аналитическая и ![]()
(c) ряд Лорана (64) имеет бесконечное число слагаемых с положительными степенями, то называется существенно особой точкой функции .
Пример 5-8. Определить характер особых точек следующих функций:
1. 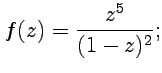 2.
2. 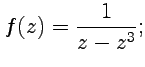 3.
3.  4.
4. 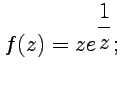 5.
5. 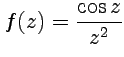 .
.
Решение. 1.
Предельные значения  и
и  ,
следовательно, точки
и
являются
полюсами. Видно, что функция может быть
записана в форме (63):
,
следовательно, точки
и
являются
полюсами. Видно, что функция может быть
записана в форме (63):
![]()
![]() является
аналитической функцией и
является
аналитической функцией и ![]() .
Следовательно, точка
является
полюсом второго порядка,
.
Следовательно, точка
является
полюсом второго порядка, ![]() .
Для точки
функция
имеет вид (65):
.
Для точки
функция
имеет вид (65):
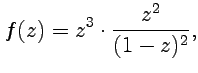
где 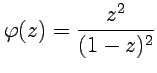 -
аналитическая в точке
и
-
аналитическая в точке
и ![]() .
Следовательно, точка
является
полюсом третьего порядка.
.
Следовательно, точка
является
полюсом третьего порядка.
2.
Решая уравнение ![]() ,
получим
,
получим ![]() ,
, ![]() ,
, ![]() .
Функция может быть записана в виде
.
Функция может быть записана в виде  .
Сравнивая с (63),
получаем, что все особые точки функции
являются полюсами первого порядка.
Точка
является
устранимой особой точкой, так как
.
Сравнивая с (63),
получаем, что все особые точки функции
являются полюсами первого порядка.
Точка
является
устранимой особой точкой, так как  ,
а в окрестности
функция
не имеет особых точек.
,
а в окрестности
функция
не имеет особых точек.
3.
Уравнение ![]() имеет
корни
,
и, как следует из (63),
они являются простыми полюсами (
имеет
корни
,
и, как следует из (63),
они являются простыми полюсами (![]() ).
Для
).
Для
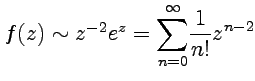 ,
т. е. ряд Лорана содержит бесконечное
число слагаемых с положительными
степенями
и,
следовательно,
-
существенно особая точка.
,
т. е. ряд Лорана содержит бесконечное
число слагаемых с положительными
степенями
и,
следовательно,
-
существенно особая точка.
4. Разложим функцию в ряд по степеням :
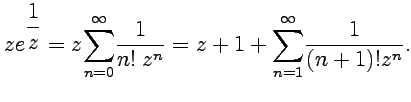
В окрестности ряд Лорана содержит бесконечное число отрицательных степеней, следовательно: - существенно особая точка функции. Из полученного разложения также следует, что является полюсом первого порядка.
5. Пользуясь разложением функции в ряд Тэйлора, получим
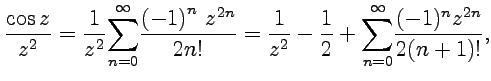
и тогда точка - полюс порядка 2, - существенно особая точка.
28-30)
6.1. Определение вычета
![]()
Вычетом функции в изолированной точке называется интеграл
|
(66) |
где
-
замкнутый контур, содержащий одну особую
точку
. Эквивалентное
определение вычета можно получить,
сравнивая (66)
с выражением для коэффициентов ряда
Лорана (61),
тогда вычетом
функции
называется
значение коэффициента ![]() ряда
Лорана в окрестности точки
:
ряда
Лорана в окрестности точки
:
|
(67) |
Из
определений вычета следует, что если
-
правильная точка функции
,
то ![]() .
Если точка
является
полюсом, то удобно рассмотреть отдельные
случаи:
.
Если точка
является
полюсом, то удобно рассмотреть отдельные
случаи:
-полюс первого порядка:
|
(68) |
так
как в случае полюса первого порядка
функция может быть представлена в
виде  ,
причем
-
ноль первого порядка функции
,
то
,
причем
-
ноль первого порядка функции
,
то
|
(69) |
-полюс порядка :
|
(70) |
Вычетом функции в точке называется интеграл
|
(71) |
причем
во внешней части контура
функция
не
имеет особых точек, находящихся на
конечном расстоянии от
.
Эквивалентно, с помощью коэффициентов
ряда Лорана в окрестности бесконечности,  .
.
|
(72) |
На
основе этих определений можно показать,
что имеет место следующая теорема:если
функция
является
аналитической на полной комплексной
плоскости, за исключением конечного
числа особых точек (включая бесконечную) ![]() ,
тогда
,
тогда
|
(73) |
Пример
6-1. Найти
вычеты функции 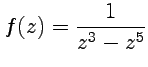 относительно
всех изолированных особых точек.
относительно
всех изолированных особых точек.
Решение. Функция
имеет следующие особые точки:
-
полюс порядка 3; ![]() -
простой полюс (
),
-
устранимая особая точка.
-
простой полюс (
),
-
устранимая особая точка.
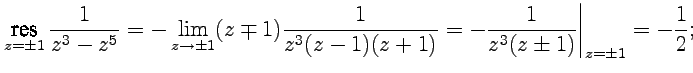
либо с использованием (69):

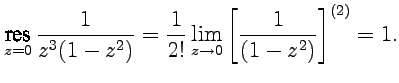
Вычет для точки можно получить, разложив функцию в ряд Лорана по степеням :
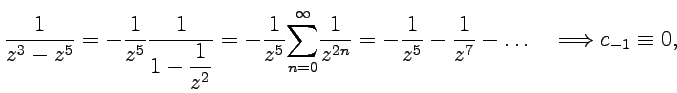
и
тогда ![]() .
Вообще, если
является
нулем порядка выше единицы, то вычет
функции равен нулю. Как видно, сумма
всех вычетов, включая бесконечную точку,
равна нулю:
.
Вообще, если
является
нулем порядка выше единицы, то вычет
функции равен нулю. Как видно, сумма
всех вычетов, включая бесконечную точку,
равна нулю:
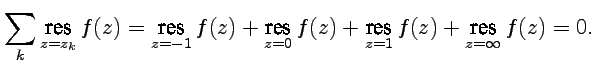
Пример
6-2. Найти
вычет функции 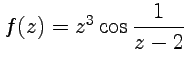 в
точках
в
точках ![]() .
.
Решение. Точка ![]() является
существенно особой точкой функции, и
поэтому вычет необходимо вычислять как
коэффициент
ряда
Лорана, т. е. на основе определения (67).
Тогда, учитывая, что
является
существенно особой точкой функции, и
поэтому вычет необходимо вычислять как
коэффициент
ряда
Лорана, т. е. на основе определения (67).
Тогда, учитывая, что
![]()
и ряд Тэйлора для , получим

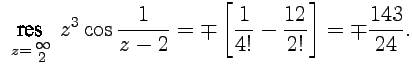
Пример
6-3. Вычислить 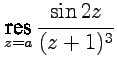 в
точках
в
точках ![]() .
.
Решение. Точка является полюсом третьего порядка, следовательно:
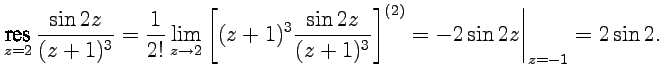
Так как в области нет особых точек, кроме , то вычет в бесконечности можно получить из условия (73):

Пример
6-4. Найти
вычеты во всех особых точках функции 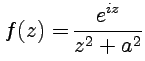 .
.
Решение. Так как точки являются простыми полюсами функции, то
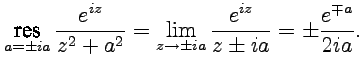






 2.
2.  3.
3. 

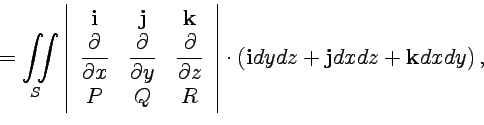

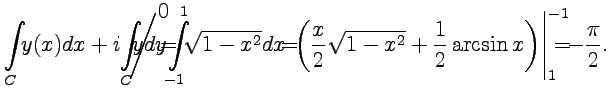


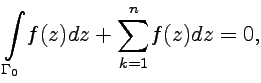


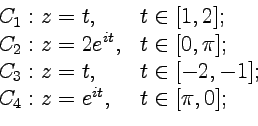
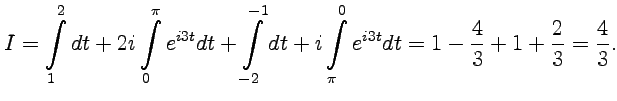




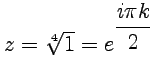 ,
,