3. Циклічні групи.

Озн. Підгрупа , що складається з усіх степенів ел-та a (усіх кратних числу a, якщо адитивна форма запису) назив. циклічною групою, породженою елементом a.

Пр-ди. М={1,2,3}

a)

Підгрупа -?

Озн. Якщо G-група і ел-т a є G, то порядок підгрупи (a) наз. порядком ел-та a.

Озн. Група G наз. циклічною, якщо вона збігається з однією із своїх циклічних підгруп. (Пр-д: (Z; +; ‘)-циклічна при (1))

Т-ма1. Для кожної цикліч. групи G справдж. одне з 2-х: або G-нескінченна. або існують такі числа, що (m<>0)

Озн. Якщо , наз. правим суміжним класом групи G за підгрупою Н, а саме розбиття наз. правостороннім розкладом групи G за підгр. Н

Пр-д (Z; +; ‘) G=Z H=(4)={…,-8,-4,0,4,8,…}

b=a+h (h=4k) Розгул. мн-ну g+H

0+H=0`: 1+H=1`; 2+H=2`; 3+H=3`; 4+H=H

Z=0`+1`+2`+3`-розклад групи за підгрупою

Озн. Кількість суміжних класів групи G за підгрупою Н познач. (G:Н) і наз. індексом групи G за Н

(G:Н)=s | G |=n, | H |=k≤n

n=k∙s  | G |= | H |∙(G:Н) (G:Н)=|G|/ |H|

Ми довели теорему(Лагранжа): В скінченній групі G порядок будь-якої її підгрупи є дільником порядка групи.

Озн. Підгр. Н гр.. G наз. нормальним дільником гр.. G якщ0 для довільного ел-та гр.. G і h єH.

Пр-ди. Будь-яка підгрупа абелевої групи

Т-ма(Критерій норм. дільника).

Озн. Сукупність усіх суміжних класів гр.. G наз. фактор-множиною

Введемо дві операції.

Т-ма: -група (Фактор-група)

Озн. Ядром гомоморфізму наз. мн-ну усіх прообразів нейтрального елемента

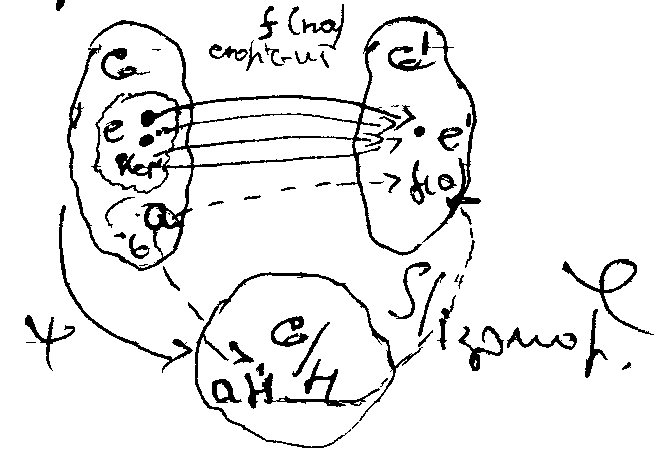
Т-ма: Нехай f гомоморфізм гр. G на гр.. G’ з ядром гомоморфізму Н=Ker f, тоді фактор-група G/Н ізоморфна групі G’

4. Означення і приклади кілець. Найпростіші властивості кілець Гомоморфізми та ізоморфізми кілець

Означення 1. Алгебра K = <  K , + ,  ,· > з двома бінарними операціями –до­давання (+) і множення (·) та однією унарною операцією () називається кіль­цем, якщо її операції задовольняють аксіомам:

1) алгебра <  K , + , > – адитивна абелева група ;

2) операція множення асоціативна

3) операція множення дистрибутивна відносно операції додавання,

Означення 2. Якщо операція множення в кільці К – комутативна, тобто

,

то кільце називається комутативним.

Властивості. 1. Так як кільце є адитивна абелева група, то всі властивості цієї групи є властивостями кільця, а саме:

а) в кільці існує i, тільки один, нульовий елемент;

б) в кільці для будь-якого елемента а існує, і тільки один, протилежний йому елемент – а;

в) в кільці сума n елементів кільця не залежить від способу розстановки дужок і від порядку слідування доданків;

г) якщо а+b=а+с, то b=с;

д) рівняння а+ х=b має єдиний розв’язок х=b – а.

2. Із 2) та 3) аксіом кільця випливають такі властивості:

а) (а₁+а₂+…+а_n)b = а₁b+а₂b+…+а_nb;

b(а₁+а₂+…+а_n) = bа₁+bа₂+…+bа_n;

(а₁+а₂+…+а_n)(b₁+b₂+…+b_m) = а₁b₁+а₁b₂+…+а₁b_m+а₂b₁+…+а_nb_m .

Означення 3. Алгебра K ₁= <| K₁|, + , – ,·> називається підкільцем кільця

K = <| K |, + , – ,·>, якщо:

1) |K₁| |K|;

2) a,b |K₁| [a+b |K₁|];

3) a,b |K₁| [a·b |K₁|];

4) a |K₁| [–a |K₁|].